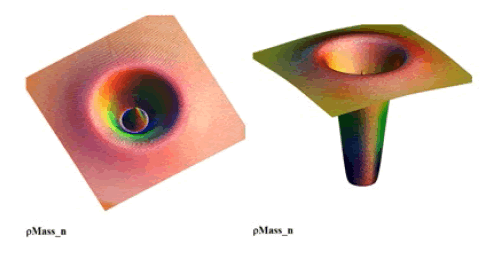Research
, Volume: 13( 6)Transformation of the Primordial Universe
- *Correspondence:
- Dale. R. Koehler
Sandia National Laboratory (retired), Albuquerque, Sandia Park, United States
E-mail: drkoehler.koehler@gmail.com
Received date: June-15-2024, Manuscript No. tsse-24-138537; Editor assigned: June-17-2024, Pre-QC No. tsse-24-138537(PQ); Reviewed: June-18-2024, QC No tsse-24-138537, Manuscript No. tsse-24-138537(R); Published: July-30-2024, DOI.10.37532/2320-6756.2024.13(6).363
Citation: Koehler.D Transformation of the Primordial Universe. J Space Explor.2024;13(6).
Abstract
A geometric-model of the Universe is physically manifest as a mathematical solution to the supplemented-Riemann equations (Geometric distortions), and displays • No geometrically-mathematical "infinities", • Mimics in one function all forces (gravitational, electromagnetic, weak-force and strong-force), • Describes Black Holes, Blackness and charged Holes and • Creates a non-classical dominating magnetic-field component (important to galaxy structure formation), • Shows a well-behaved metric while providing a geometric rendering of the Fermi-constant, the weak-force strength-constant, and • Establishes and emphasizes the geometric-curvature and energy-density extrema concepts, said concepts constraining the Universe’s explosive-matter-creation-time to 1-DAY (86,400 sec.) while energetically generating all fundamental matter-energy creation products (electrons to muons to bosons to holes). Water and carbon dioxide are created in the following 2–3-DAY time interval while the formation/destruction time for protein structures is 6-DAYS given a 5.3(10)4 Joules/m3 “remnant-creating-form” of the exploding Universe energy-density.
Keywords
Cosmology; Classical field theory; Classical mechanics; Riemannian Geometry; Structural stability; Black holes; Physical constants
Introduction
We use the Riemannian geometric equations with a supplementary "material-like" descriptor-equation T44 = −T11−T22−T33 to describe geometrically-energetically-distorted regions of space [1], therefore there is NO ad hoc "matter + nothingness" modeling. The material limits of such a region of space are manifest as “extrema geometric-curvatures" (distorted space i.e., Distorted Geometry (DG)). In addition to having earlier described fundamental-particle structures, we posit here a “Universe evolution” scenario wherein the detailed physical features include structural characteristics, creation energy-density limits and creation-times.
We calculate the equipartitioned Universe energies at:
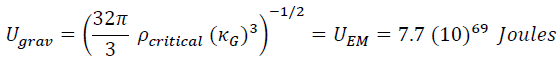
and the Universe (gravitational body) radius ≡ 2κGUgrav = 1.27(10)26 meters. The radius of the Universe (electromagnetic body) is calculated at 2κEM UEM = 1.3(10)13 meters after having used Friedmann’s critical density, (ρ_critical energy-density = 8.898(10)-10 J/m3), for the gravitational energy-density and ρ_electron (8.74(10)29 J/m3) = the ρ_critical energy-density for the geometric-electromagnetic extremum. Emphasis has been placed on the concept of “geometric extrema”, that is, curvature and energy-density extrema. This geometric-material concept constrains the explosive-matter-creation-time to 1-DAY (86,400 sec.) while energetically generating all fundamental matter-energy creation products (electrons to muons to all elemental-nuclei to bosons to holes). Atomic water and carbon dioxide are created in the following 2 DAY-3 DAY time interval.
With application at the “macro” scale, we describe "a Universe creation process” as an alternative-model to big-bang representations.
It has been shown in the present work that the distorted-space, or Distorted Geometry (DG), model of matter, can be configured as a composite gravitational-and EM-energy based structural description of the Universe, that is, geometrically distorted regions of the spacetime manifold can be realized to produce structures satisfying Universe dimensions and energies with temporal development based on energy conserving, time-based transition dynamics.
For a timeline of the Universe development, as prescribed and predicted by the mathematics of the model, two energy-dense spheres (a gravitational outer sphere and an EM inner sphere) are formed. The smaller, inner EM (electromagnetic) sphere is originally (when was it created?) stable, that is, stable defined as existence at a “geometric structural-stability extremum”, but the sphere is perturbed (the beginning of this Universe) to implode from a radius of 1013 meters to a radius of 106 meters, the second geometric (material) extremum, (the material will not sustain energy-densities or geometric-curvatures greater than, or beyond, this extremum). The implosion requires a period of 0.5 DAY (43,200 seconds).
The unstable imploded intermediate state explodes, expanding radially past the geometric-electron extremum-state, (an energy-density state of 8.74(10)29 J/m3), in another 0.5 DAY! NO fundamental energy-dense structures (the matter-energy-density limits between the electron mass-energy-density and the boson mass-energy-density) are created after this point in the expanding Universe-sphere, that is, the dissociation-energy-density of the expanding Universe-sphere will no longer create/destroy matter-energy structures, other than compound structures with structural energy-densities less than that of the electron rest-mass-energy-density of 8.74(10)29 Joules/m3.
Distorted Geometry (DG) (see references [1-23]) mimics of electrons, muons, muonic-protons, neutrons [14], the chemical Elements, and baryonic- and electronic-holes are created during the latter-half, the explosive half, of the one-day time period. High energy, short lifetime structures are surely created but decay immediately ( <10−27 sec.) to the more stable entities just delineated. Of particular note are the large “hole structures” posited as electronic- and muonic-energy-density, distorted-geometry mimics of classical electromagnetic or baryonic structures.
Atomic and molecular structures are composites of these created fundamental geometric structures and are composed after the 1-DAY creation process, when the expanding Universe-energy-density has cooled enough to disallow structure-destruction. For example, H2O- and CO2- production are manifest on DAY-3 while the formation/destruction time for protein structures is 6-DAYS given a 5.3(10)4 Joules/m3 “remnant-creating-fraction” of the Universe energy-density.
A distorted (material) geometry ≣ The universe energy
It is shown in the present work that the distorted-space geometric-representation of matter can describe the origin and creation of the Universe, a model of an originally stable, geometric-energy-distribution which transitions, via implosion and subsequent explosion, to a newly-created matter-stage which mimics the presently observed Universe. We use the verbiage “distorted” to communicate the concept of “energetic-manifold-warping” and to distinguish “spatial-warping” from “classical matter-warping”, although the concept of “matter” is in fact, in the present “distorted-geometry” model, the “localized geometric distortion energy” of the spatial manifold itself without a classical “matter stress-energy source”.
The distorted-geometry (DG) energy-density function (see the earlier references but, in particular, reference [1]) is a descriptor which has been employed to characterize primordial generation of the matter structures, i.e., the Elemental nuclei, holes (large mass structures) and fundamental congregated structures such as the atomic Elements, and H2O-, CO2- etc. molecular structures.
An artistic rendering (time-development) of such a phenomenon is depicted here and mathematically graphed in FIG. 1-7.
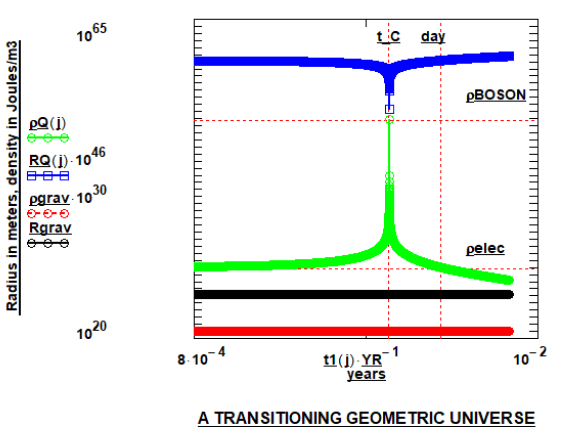
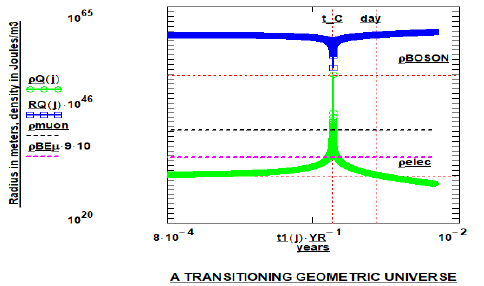
Figure 1: The Universe’s gravitational (Rgrav) component non-transitioning-radius and the radius of the EM (RQ) component as a function of time; ordinate in meters and abscissa in years. The contracting and post-collapse expanding electromagnetic energy-density shell is displayed as ρQ in Joules/m3. The gravitational energy density” =ρgrav with magnitudes of Joules/m3. The “time notation,” “day,” is included to highlight the magnitude of the time range to allow “baryonic and gravitational” energy production; t_C is the time to collapse of the EM sphere. The extremum energy-densities are indicated as ρBOSON and ρelec.
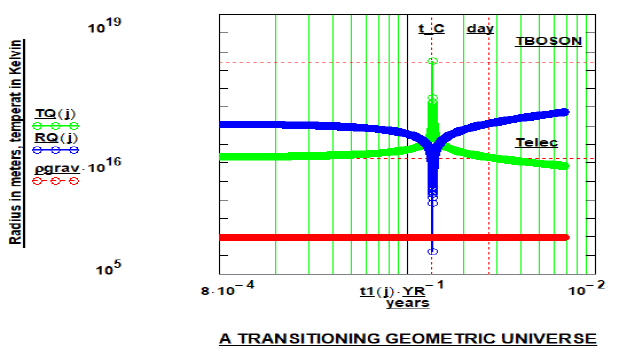
Figure 2: The Universe’s gravitational (Rgrav) non-transitioning component as a function of time; the ordinate is in meters and the abscissa in years. The radius of the contracting and post-collapse expanding electromagnetic energy shell is shown as RQ. The temperature of the electromagnetic energy shell is displayed as TQ(j) in Kelvin units with the associated energy-density as ρQ in Joules/m3 units. The “time notation,” “day,” is included to highlight the magnitude of the time range to allow “baryonic and gravitational” energy production; t_C is the time to collapse of the EM sphere. The extremum-temperatures are indicated as TBOSON and Telec.
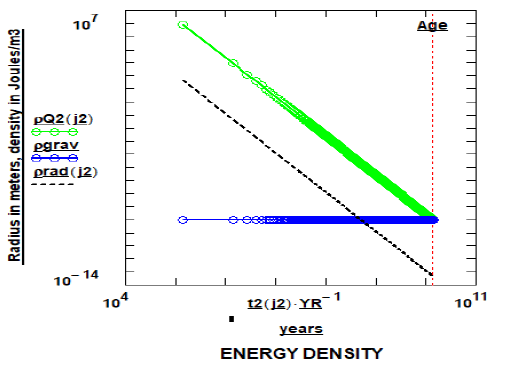
Figure 3: Transitional energy densities are displayed as the Universe’s gravitational component (ρG) and the electromagnetic components (ρQ2 and ρrad) and are plotted as a function of time after 104 years.
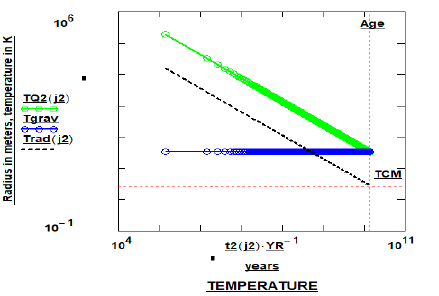
Figure 4: The Universe’s gravitational (Tgrav) and electromagnetic (TQ2 and Trad) component-transitioning-temperatures are illustrated as a function of time. The extremely hot EM core has cooled to the presently observed cosmic-microwave-radiation temperature TCMB, a background temperature of 2.726K. The “Universe-time” Age =13.77(10)9 years and the cosmic microwave background CMBR black body temperature is denoted as TCM.
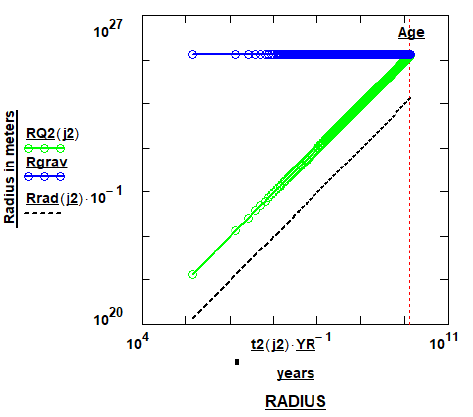
Figure 5: The Universe’s gravitational (Rgrav) and electromagnetic (RQ2 and Rrad) component-transitioning radii are plotted as a function of time, ordinate in meters and abscissa in years. The gravitational radius is calculated from the Friedmann Critical Density, ρ_critical = 8.9 × (10)-10 Joules/m3. The radius of the expanding radiation sphere is coincident with the radius of the baryonic- or observable universe sphere but is offset for display purposes.
Figure 6: The Universe’s radius of the EM (RQ) component as a function of time; ordinate in meters and abscissa in years. The contracting and post-collapse expanding electromagnetic energy-density shell is displayed as ρQ in Joules/m3. The “time notation,” “day,” is included to highlight the magnitude of the time range to allow “baryonic and gravitational” energy production; t_C is the time to collapse of the EM sphere. The extremum energy densities are indicated as ρBOSON and ρelec with a muon-creation energy-density shown as ρmuon and the Binding energy density of the muons in the posited muon-structured proton shown as ρBEμ.
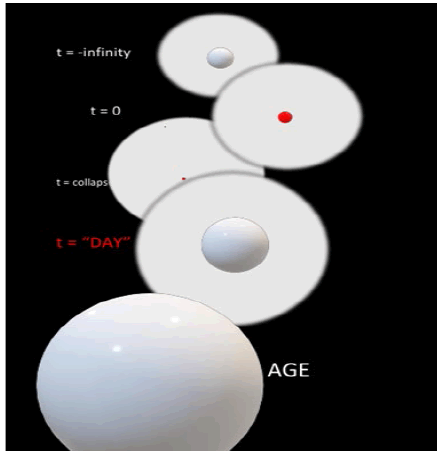
This is a classical attempt to show a "time changing" series of events with a "static" "artistic" display of figures (spheres). The "top" figure (labelled “t=-infinity (-∞)”), represents the earliest time with the larger sphere (radius =1.27(10)26 meters) representing the "gravitational" distribution of Universe energy, while the smaller inner sphere (radius =1.3(10)13 meters) represents the "geometric-electromagnetic" distribution of Universe energy. The construction of the “electromagnetic-energy” sphere results from utilizing a “Distorted Geometry (DG)” compound “geometry-to-energy” coupling-constant, a latter-day construct for describing ANY energy-bearing structure; you cannot describe an electron structurally without this (DG_EM) geometry-based component.
We have calculated the Universe (gravitational body) radius ≡ 2κGUgrav = 1.27(10)26 meters and the Universe energies at
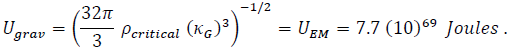
The chronology starts with the inner electromagnetic sphere collapsing to a radius so small that you cannot really show it on such an artistic rendering (radius = 1.5(10)6 meters), where the next time-evolving spheres labelled t=0 and t=collapse are intended to represent this collapsing process. Then, the inner (next) sphere explodes (expands); this is the stage where the definition of the DAY occurs. It is determined from the basic Distorted-Geometry model of matter which has been applied to describe the electron, the muon, the boson, holes, and radiation, all the building blocks of matter and now at the dimensions of the Universe [1]. Finally, the 5th sphere rendering shows the condition where the inner sphere has expanded to the diameter of the outer sphere, a condition representing the EM and gravitational Universe at a diameter of 1.27(10)26 meters! An “energy-conserving-explosive process,” as an alternative to “expanding space” structural-modeling, is manifest as an energetically unstable Universe, an originally stable but subsequently collapsing state, followed by an explosive expansion. The energy transition dynamics are described for a spherical, gravitational, and electromagnetic, geometrically-based mimic of matter existing at quantitative measures of a size just delineated.
The composite coupling-constant and the geometric universe
We have modeled the structure with a compound, two-component, geometric-coupling-constant, with all states defined by the compound form-

For the geometric structural-mimic of the electron, the electron-radius 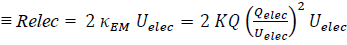 where
where 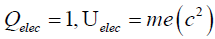 me is the mass of the electron, α = fine structure constant where
me is the mass of the electron, α = fine structure constant where 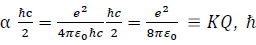 Planck’s constant, G is the gravitational constant and c is the velocity of light. Classically, the electron is an “electromagnetic” structure characterized with “electromagnetic” descriptors, however in this “distorted or warped geometry” modeling (possible by virtue of a solution to the Riemannian geometric equations, after ascribing a material quality to localized “distorted or warped” regions of the geometric manifold), these electromagnetic descriptors are understood as sourced in geometric terms such as the magnitudes of the 1/r4, 1/r6 , and 1/rn structural, tensorial-features of the energy-density elements and unlike classical Newtonian and Einsteinian 1/r2 energy-density descriptions of gravity and electromagnetism, the DG formalism exhibits energy-density functional-zeroes particularly at the geometric origin and therefore exhibits no “geometric infinity”; see Appendix for the mathematics, and the insert below for a 2-D plot of the geometric-structural energy-density component, T44(muon), as a visualization-help FIG. 8.
Planck’s constant, G is the gravitational constant and c is the velocity of light. Classically, the electron is an “electromagnetic” structure characterized with “electromagnetic” descriptors, however in this “distorted or warped geometry” modeling (possible by virtue of a solution to the Riemannian geometric equations, after ascribing a material quality to localized “distorted or warped” regions of the geometric manifold), these electromagnetic descriptors are understood as sourced in geometric terms such as the magnitudes of the 1/r4, 1/r6 , and 1/rn structural, tensorial-features of the energy-density elements and unlike classical Newtonian and Einsteinian 1/r2 energy-density descriptions of gravity and electromagnetism, the DG formalism exhibits energy-density functional-zeroes particularly at the geometric origin and therefore exhibits no “geometric infinity”; see Appendix for the mathematics, and the insert below for a 2-D plot of the geometric-structural energy-density component, T44(muon), as a visualization-help FIG. 8.
In this geometric description of the particle structures, it is possible to point to well-defined geometric features as opposed to arbitrarily defined features as, for example, we define two Coulombic energy-density features as “radii” which are “zeroes” in the “electric F142 field” and the “magnetic Fmag2 field”, a description which is not possible with “classical 1/r2 field” descriptions. We use the “geometric electric-field zero” as the “particle radius” descriptor throughout the manuscript.
This perspective “points to” the origination of “EM charge” and “gravity,” as well as “beta decay” and the “strong nuclear-core force,” to be “generated” by “distortions” of the geometric manifold.
Additionally, the geometric equations giving rise to the energy-density descriptors are non-linear and coupled so that the classical models of independent constructs are not appropriate in this modeling. A particularly important feature which improves on the classical 1/r2 or 1/r3 description of “forces”, or “energy densities, or pressures”, is this absence of “singularities”, that is, there are no infinities at the geometric origins of the distortion features.
Since the “structural mimicking” is an “energy-density magnitude-simulation”, that is, with ρG ≡ energy-density, then ρG_Universe-minimum = ρG_electron = ρG_black-hole-minimum and ρG_Universe-maximum = ρG_boson = ρG_black-hole-maximum; these nuclear or fundamental-particle determined, Distorted-Geometry (DG)-based, geometric-curvature-extrema are basic to geometric fundamental particle and primordial black holes characterization. When the post-collapse, t=0.5 DAY to 1.0 DAY, energy-densities of the Universe-structural-components are within this extrema-defined energy-density range
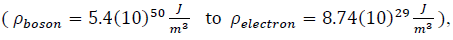
all energy-density defined gravitational and electromagnetic structures can be generated (created); the geometric extrema are curvature and energy-density extrema. The Universe energy-defined structure contracts (@ t ≡ 0) and expands complexly at (or near) velocity c (energy propagation is proportional to energy-density of medium).
A collapsing initial-phase-1 state, posited as the inner-sphere of a Distorted-Geometry (DG) configuration with two equal-energy species or energy-density states, electromagnetically transitions, via an intermediate “mediator” state (mimic of the W-boson structure in beta-decay), to a final 3-component state (ala a mimic of the beta-decay transition process), with all states defined by the compound coupling-constant described above. The constant-U condition is posited via the time dependency equations for the radial description of a DG-geometric, Schwarzschildian, EM + gravitational, form of the Universe;
Runiv(DG) = 2(κG+ κEM)U and dR/dt = 2(κG dU/dt + κEM dU/dt + U dκEM /dt) with dU/dt = 0.
The originally stable Electromagnetic (EM), inner sphere of the initial state, one of the two species, is perturbed and initiated to collapse to an energy-density represented by the posited DG-geometric-maximum-curvature limit of the geometric manifold. The time changing features of the electromagnetic sphere are the “charge quantity Q” and the collapsing spherical radius (outlined above); no feature of the gravitational structure allows for time dependence given a dU/dt = 0 descriptor and therefore, the gravitational enveloping sphere remains static to maintain the constancy of energy.
The collapsed unstable extremum bosonic-structure, an energy-dense structure (~1050 Joules/m3) and terminator of the implosion process, explodes (for comparison, the lifetime of a boson is Heisenberg-limited to ~4.2(10)-27 seconds (ΔU Δt > ℏ/2)) while the experimental half-life cited for bosons is 3(10)-25 seconds and therefore satisfies the Heisenberg supposed half-life limitation. The energy-propagation (geometric) time across the boson radius is 1.4(10)-27 seconds (assuming velocitypropagation =c), a result comparable in magnitude to the Heisenberg limit (?); the boson experimental half-life (3(10)-25 sec.) is approximately 214 times the unidirectional energy-propagation time.
A similar multidirectional calculation for the lifetime of the “Universe-bosonic intermediate-state” equals 1.03 seconds; at a radius of 1.5(10)6 meters ≡ R0 (a correction necessary to (Universe Dynamics and Universe)). The collapsed “intermediate state” condition is one wherein all the original-EM distorted-geometry region has been concentrated into a mimic of the fundamental-particle extremum, the W-Boson mediator-state of “nuclear beta-decay.” This distorted “intermediate-state” geometric body is characterized as an “extremum geometric-curvature" body which subsequently and unstably explodes as an electromagnetic (κEM) energy-dense form.
The post-collapsed or expanding Universe-state is a mimic of the 3-component post-collapsed neutron-state, which is a muonic-proton (5 anti-muons (+) and 4 muons (-)) (see protons as geometric distortions) plus an electron and a neutrino, mimicked as a {1} static gravitational (κG) sphere enveloping {2} an EM-like (κEM) spherical-structure with an accompanying {3} radiation-sphere (κEM).
By mimicking the electron’s energy-density as an initial condition for the Universe EM component, we can calculate the equivalent EM-electric-charge as QEM = - 2.1(10)55; QEM in the collapsed bosonic-state is -7.1(10)51. Expanding at velocity c, the attenuating (?) geometric-electromagnetic-sphere propagates to the Universe gravitational radial boundary and is reflected upon itself via the radiation (optical EM) phenomenon of Total Internal Reflection (TIR). Interestingly, the expansion time to reach the gravitational-sphere radius (≡ Rgrav ) is
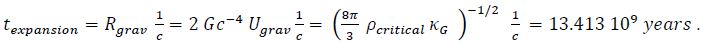
If the presently accepted “age of the Universe” = 13.787 ± 0.02 (10)9 years is correct, then the leading-radial-edge of the DG-Universe is now collapsing after TIR. Or, alternatively, if “age of the Universe” ≡ “texpansion,” then energy-propagation from r = 0 to r = Rgrav is not at velocity = c. One could, alternatively, use a modified Friedmann ρcritical accordingly.
Geometric Mass-Energy Production Physics
Geometric structures
Universe energies have been classically subdivided according to the experimental astronomical data wherein “observable baryonic matter” = 0.049 UUniv. In the present DG-geometric model, we have ascribed to the “geometric extrema” the distorted energy-densities of the electrons, muons, and holes. For holes and all DG-particle structures, as rendered in the geometric formulation, the “geometric-structural-solution [1],” a universal all-matter-solution, extends from “radius = 0 to radius = ∞”. The core-region, r <2 κEMUEM, is considered “black” due to ”TIR” [1] (Total Internal Reflection) since the energy-density is greater (non-uniformly) inside the core-region of the DG-structures. However, the velocity of energy-propagation in this material-DG-medium is a function of the metrics [1], that is 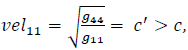 , and is an example of the physics expressed in references[21-23]; “faster-than-light propagation is possible without requiring moving objects to have imaginary mass.
, and is an example of the physics expressed in references[21-23]; “faster-than-light propagation is possible without requiring moving objects to have imaginary mass.
Holes are massive, geometric-extrema, DG-energy entities at densities ρMuon and ρelectron. This ascription leads to a definition of “baryonic” therefore as “muons + electrons + muonic-protons + muonic-neutrons + muonic-holes + electronic-holes + all congregated Elemental forms thereof” i.e., all matter. The present-day massive-energy galactic-envelopes.” surrounding the holes are considered formed of “baryons.”
With a “muonic galactic envelope” surrounding either a muonic- or electronic-core-hole posited as the structure of “all galaxies” and with the envelope posited as the dominant energy-constituent of “all galaxies”, we have modeled the galaxy masses as constituting (with the hole-masses) the whole of the Universe energy (minus the relatively negligible radiation component), with particular emphasis on the muonic-and electronic-structures as the primary building blocks. This model of a geometrically-constrained Universe (extrema curvatures for stability) produces structures which originate from the fundamental, “geometry-to-energy” coupling-constant,
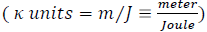
and from the resultant “geometric-matter-solution” [1]. The model has given rise to a “geometric muonic and electronic” description of protons, neutrons, and all congregated Elemental structures. Although the core-hole feature of the galaxy structure seems to be the “congregating power,” the main component of the galaxy-mass-energy lies in the “attracted” envelope masses. Examination of the “fundamental-particle” table for leptonic baryons suggests a mass-energy hierarchy from “electron to muon to tauon to…”,
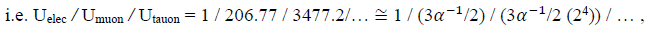
which inferentially suggests for a “stability-based” 2-component, muonic/anti-muonic and electronic/positronic energy-density distribution (since antimatter survives during creation) in the “extremum-limited” energy range of the “Universe DG mimicking”. Consideration of Heisenberg “energy-based” structure-lifetimes also supports the suggestion.
The muonic-energy-density-mimics are twofold and defined as {1}, “galaxy-muonic-core-holes” ≡ n2 UMuonHole @ a mass-energy density = ρMuon and {2}, “protonic and neutronic structures throughout galaxies” ≡ n1 UMuon; the electronic-energy-density-mimics are defined as {3}, “galaxy-electronic-core-holes” ≡ n4UelectronHole @ a mass-energy-density = ρelectron and {4}, “electronic structures throughout galaxies” ≡ n3 Uelectron.
The “mathematical” development of the distorted-geometry (DG) model, with its geometric structures, is presented in the Appendix. Although we have assumed the proton-structure as muonic, we posit that the Universe energy-density had “compressed” the muonic-structures since
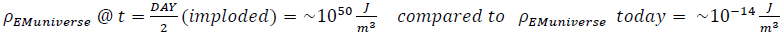
and therefore the primordial-proton was structured and “fundamental-like” with compressed-structural “Muons”, that is,
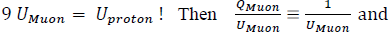
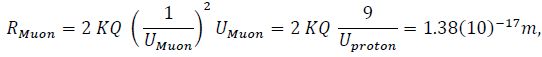
which is a slightly less-massive (UMuon =1.67(10)-11 J compared to Umuon = 1.689(10)−11 J), lesser-curvature structure with density expressed in Eq.(1);
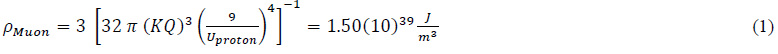
compared to 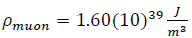 muonic “extrema-energy-density-mimics” culminate production in this exploding Universe at the mass-energy-density ρMuon.
muonic “extrema-energy-density-mimics” culminate production in this exploding Universe at the mass-energy-density ρMuon.
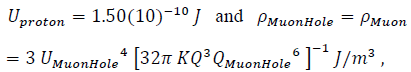
or since
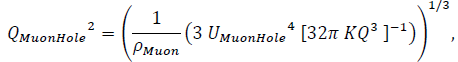
then
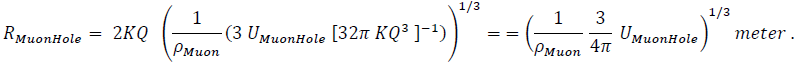
For a tauonic-like structure,
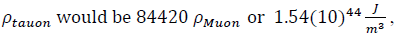
existing, at present-day with an extremely short half-life and not established as a “stable” entity, but was more stable at “Universe energy-densities” near t = DAY/2.
The proton result constitutes a revision of the “proton-structure binding-energy” calculations presented in reference [14].
Electronic “DG extrema-energy-density” mimics, assuming no radial compression at tformation/destruction = 1 DAY, are manifest at (see Eq. (2)),

and
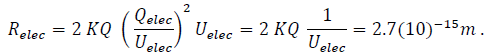
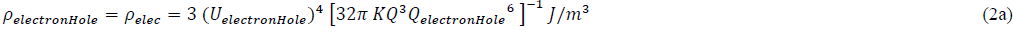
If the UelectronHole structures are stable DG structures.
The electronic mass-energy density is an “extremum” mass-energy density while the muonic mass-energy density is a “stable” “non-extremum” value (muon half-life at present-day Universe mass-energy density =2.2(10)-6 seconds). As the structural foundation-element of the proton, the energy-density background of a nine-muon configuration constrains the muon-structures to stability.
Mathematical Methods and Results
Particle formation
We employ the Van’t Hoff chemical concept of “association/dissociation” at the “nuclear-Universe” level to describe the energetics of “Universe-particle-creation,” given a more expansive interpretation of “association/dissociation” as “creation/destruction” or “formation/destruction.” Then the particle “association/dissociation” time ≡ the time when the exploding
“Universe energy-density = particle energy-density”
(at the formation/destruction-time tfd), and occurs when
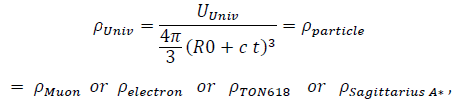
“a production-requirement of only the quantized stable entities.” The “formation/destruction” time for muonic-holes would be “that of the Muons.” The “formation/destruction time” for electronic-holes would be “that of the electrons” for the same reason. We write when ρparticle ≡ ρelectronHole , for example,

After this time, the Universe energy-density (via both the creation- and destruction-processes) can no longer “destroy” the “nuclear particles” (includes the massive “hole” structures) thus created.
Modeling the dynamically changing Universe as a mimic of a “radiating black-body,” with the associated energy change, can be abstractly considered as an alternative to this “formation/destruction” formulation, although in such a “statistical mechanics” mathematical-framework the “electric, magnetic, and gravitational structural details” are unrevealed.
The resultant form of the “black-body” time changing energy-function is illustrated in Eq.(3a);
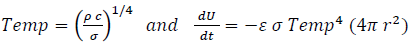
where we are considering a radiating sphere with radius r. Explicitly including the energy U, with ρ ≡ ρ0 = constant, and an emissivity, ε =1 , leads to
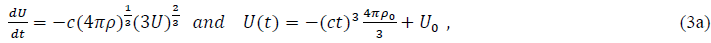
with
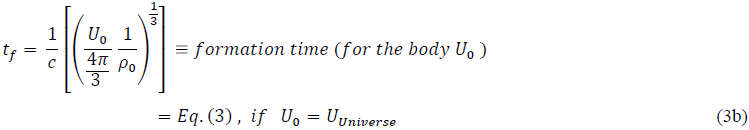
and ρ0 is the Universe energy density at time tf, which we set equal to the geometric-structure descriptor. What is classically (at significantly lower temperatures) considered as a “radiated energy U” is here considered as the “change-of-state energy” of the hot Universe-body.
This subsequent, “time-of-production” solution, Eq.(3a), for a given “black-body distortion (DG) structure”, is the same as for the “DG formation/destruction” model Eq. 3, and offers a dynamic time-dependent picture of “particle energy production” while supporting the “exploding-model” DG-EM propagation velocity “c”. It produces “energy-magnitude” results however that disagree with “conservation of charge”.
Structural formation times and physical descriptors
The formation-destruction (tfd) times, measured from time = DAY/2 = start of explosion (after a half-day of implosion), are
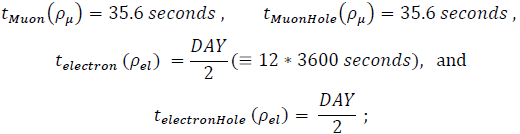
the mass-energies are
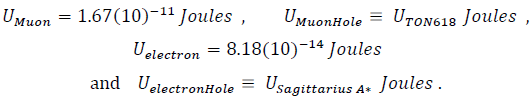
Particle structural radii, R = 2κEMU a Schwarzschildian form with an EM coupling constant, are
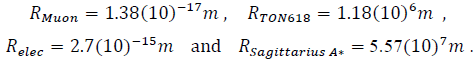
The “hole” mass energies have been approximated and defined by the astronomical experimental data.
Muon formation, the initial UUniv energy-conversion process, occurs throughout the expanding Universe-structure and subsequently initiates production of the muonic structures, the protons, and neutrons; muonic-hole production occurs simultaneously with Muon production. Muon (and muonic-hole) production ceases at 35.6 seconds;
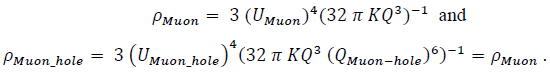
Individual particle-formation times are of interest and are qualitatively calculated as the propagation times across the structural physical radii and are arbitrarily defined here as tf(DG) ≣ t_particle-formation; with
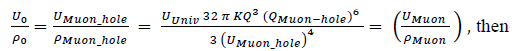
tf = 4.61 10-26 sec for the Muon and 4.13(10)-3 sec for the Muon Hole(TON618) !
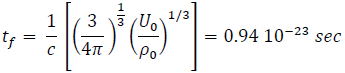
for an electron and 0.196 sec for an electron Hole (Sag)!
We have set the total energy sum of these components, as manifest in the congregated-structures, equal to the EM(DG)-Universe energy. Proton- and neutron-formation of the muonic-Element-structures and muonic-hole formation, occurs during the “total muonic-formation time-interval”.
Electronic-hole structures are completely formed by time = one day, the half-day interval after the half-day implosion. Thus, using the “formation/destruction times” Eq.3, we write Eq.4 and Eq.5 with an enumerated elaboration of the DG mass-energies (galaxy- cores are galaxy-black-holes),

Using the present-day astronomical-energy data cited above for the galaxy-energies, with the Universe data for TON618 [18], Sagittarius A* [19] and Milky Way [20] stars, one tabulates

The muonic mass energies (Muons produced by tMuon) ≡
≡ 100(or 50)*UTON618 + Milky Way stars.
The “Muonic-hole” is arbitrarily defined as TON618 and the “electronic-hole” as Sagittarius A*.
Then, with the sum of “galaxy-envelope-energies” set = n1UMuon,

where we have posited that the core of every galaxy is a black hole.
We have assumed, all muonic-nucleonic-energy is proton-energy, or neutron-energy, at a muonic energy-density = ρMuon and, for atomic production and zero net charge, the number of electrons n3 is set = number of protons + neutrons and where the electron energy is sufficiently small to be ignored at this point in the modeling.
Conservation of charge
The concept of “electric charge,” in the context of a “Distorted Geometry,” arises in a coupled way throughout the complex of equations describing the impact on the energy-densities of the material. To elucidate said impact, we rewrite, in an abbreviated form, from the mathematical Appendix, pertinent equations to show the physical impact of “electric charge” on a distorted geometry manifold;
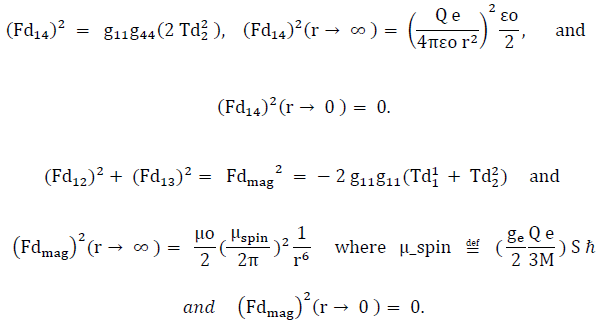
If we use as a basic physical principle, a “conservation-of-electric-charge” phenomenon (“conservation of distorted-geometry” in this model) and a phenomenon applicable to the “explosion” process,” then we can write Eq.(5), assuming all net-charge (not electron-nulled) is in the core-holes (DG muonic or electronic) structures, reflecting both the “electron-like, energy-density” of the primordial Universe inner-sphere and the posited phase-2-created “electron-Holes” and “muonic-Holes”. The DG-electric charge for the muonic-Hole is
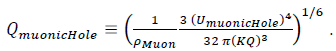
Solution of these 2 equations, ((4) and (5)), produces
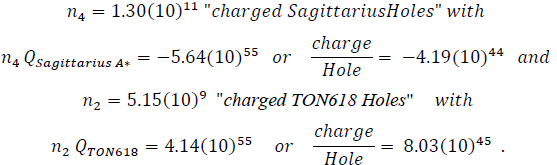
The results for the mass-energies are
Sagittarius-like Hole mass-energies = 9.61(10)64 J and TON618-like Hole mass-energies = 6.18(10)67 J. The total “Universe-electronic-Galaxy” mass is 1.469(10)69 J and the “Universe-muonic-Galaxy” mass is 6.242(10)69 J.
The envelope-energies, formed from the sum of the muonic and electronic energies, plus the smaller magnitude hole-energies, constitute the time-evolved baryonic-energies distribution.
With a muonic “envelope,” issuing from “muonic-constructed protons and neutrons” and posited as the dominant constituent of “all galaxies,” we have modeled the galaxy masses as constituting the whole (approximately) of the Universe energy with particular emphasis on muonic and electronic structures as the primary building blocks. This model of a “geometrically-constrained (extrema curvatures for stability) Universe,” produces structures which originate from the fundamental, compound “geometry to energy” coupling constant, κ = κG+ κEM , and from the resultant “geometric-matter-solution” [1]. Although the core-hole feature of galaxy structures seems to be the “congregating power in this Universe structure,” the main component of Distorted Geometry (DG) galaxy-mass-energy lies in the “attracted” envelope masses of the model’s galaxies.
Post-day formation structures and times
Subsequent to the “phase-2” matter-creation process (post DAY), it is posited that a reduced or exhausted “Universe-particle-structure energy-creation-capability” existed. Atomic and molecular structure creation was however possible and is here delineated according to the structure’s formation/destruction energy-densities. The protein molecular structure is characterized in Table-2 and H2O and CO2 structures are posited (experimentally suggested, see data) as being created simultaneously (see tabulated structural features). These results are presented in TABLES 1 and 2.
TABLE 1. Nuclear energy densities and formation times.
| Descriptors | Nuclear Energy Densities |
Nuclear- Creation Times |
|---|---|---|
| Nuclear Elemental Structures |
Formation/Destruction Energy-Density (J/m3 ) ρ = U4/(32π (KQ3)Q6) |
Formation/Destruction Time(sec): (add Implosion DAY/2) |
| DG-Muon | 1.5 (10)39 | 35.6 |
| Proton | 9.63 (10)42 | 1.92 |
| Neutron | - | 1.92 |
| Helium | 3.85 (10)43 | 1.21 |
| Carbon | 4.28 (10)42 | 2.52 |
| Oxygen | 2.41 (10)42 | 3.05 |
| Iron | 3.07 (10)41 | 6.06 |
| Uranium | 5.10 (10)40 | 11.03 |
| Muonic- hole | 1.5 (10)39 | 35.6 |
| electron | 8.74 (10)29 | DAY/2 (43200 sec) |
| Electronic- hole | 8.74 (10)29 | DAY/2 |
TABLE 2. Atomic and molecular energy densities and formation times.
| Atoms | Binding Energy-Density ρ = 3 B.E/4π(R)3 |
Creation Times If available formation-energy is 2(10)55 J |
|---|---|---|
| Hydrogen | 1.03 (10)13 J/m3 | 2.5 DAYS |
| Carbon | 1.47 (10)11 J/m3 | 2.5 DAYS |
| Oxygen | 1.34 (10)12 J/m3 | 2.5 DAYS |
| Molecules | Binding Energy-density ρ = 3 B.E/4π(R)3 |
Creation times |
| Water (H2O) | 1.48 (10)11 J/m3 | 2.5 DAYS |
| Carbon dioxide (CO2) | 1.48 (10)11 J/m3 | 2.5 DAYS |
| Protein | 5.3 (10)4 J/m3 | 6 DAYS |
The distorted-geometry (DG) energy-density function (see the earlier references [1-23] but, in particular, reference [1] ) is a descriptor which has been employed to characterize primordial generation of the matter structures, i.e., the Elemental nuclei, holes (large mass structures) and fundamental congregated structures such as the atomic Elements, and H2O-, CO2- etc. molecular structures. We have expanded on the manuscript Universe Dynamics to provide further quantitative numerical details for the Elemental-matter-energies created during the explosion process particularly for the “three and several-DAY creation time intervals”.
We posit that the energy-density function defined in Eqs.(3), (3a) and (3b) can qualitatively in form be used to model the “Distorted Geometry (DG) Elemental” matter-production process, however the boson-temperature, representing the “third-body imploded-Universe-energy-density, is 2.9(10)16 Kelvin.” The “hot Universe-energy-density” condition at all times constitutes a predominant “third-body” element for calculational purposes and therefore determines the approximate quality of such calculations. Formation/destruction energy-densities are prescribed and tabulated while understanding the importance of the presence of this intense “Universe energy-density.”
The elemental energy-densities and formation/destruction times, measured from (after) DAY/2 = the “implosion time”, are presented in TABLES 1 and 2.
Data for post-day atomic-mass-energy production
HYDROGEN; Ionization Energy = 13.6 eV (1312 kJ/mol), particle radius RH = 0.037 nm, particle energy-density = 1.027(10)13 Joule/m3
CARBON: Ionization Energy = 11.26 eV (1086kJ/mol), particle radius RC = 0.143 nm, particle energy density = 1.47 (10)11 J/m3
OXYGEN: Ionization Energy = 13.62 eV (1314kJ/mol), particle radius RO = 0.073 nm, particle energy density = 1.34(10)12 J/m3
Data for post-day molecular-mass-energy production
WATER; Binding Energy (B.E.) = 9.54 eV, particle radius
RH2O = 0.135 nm, particle energy density = 1.48(10)11 Joule/m3
CO2: B.E. = 11.4 eV, particle radius RCO2 = 0.143 nm,
particle energy density = 1.48 (10)11 J/m3
PROTEIN: B.E. = 0.0217 eV, particle radius Rpro = 2.5 nm,
particle energy density = 5.3(10)4 J/m3
With the energy-density function, Eq. (3), applied for atoms, then a formation/destruction energy-density of 1.34 (10)12 J/m3 (atomic oxygen necessary for water production) would occur at
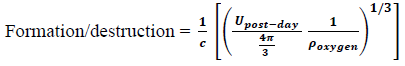
We ask, what is the “post-day” energy requirement @ t = x (x = 3 or 6) days? Answer is
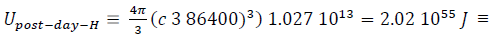
≡ Universe-energy @ post 1-DAY required for “atomic hydrogen” production.
For “atomic carbon” and “oxygen” production we calculate,
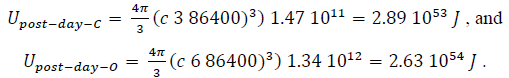
With the energy-density function Eq.(3), applied for molecules,
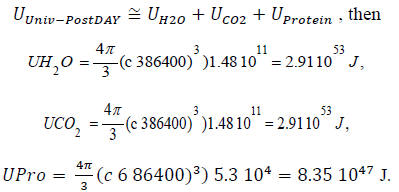
The Universe energy converted to DG fundamental-structure energies (phase-2) has been calculated with the assumption of total energy-conversion but if as little as 1055 Joules (Universe Energy ≣ UEM = 7.7 1069 J), equivalent to pp1015 (!!) of the total Universe Energy, is still present at the end of DAY-1 in the expanding Universe (e.g. CMBR energy is present @ DAY-1 @ UCMBR = 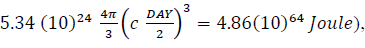 then atomic hydrogen (both muonic-protons and electrons have been produced) can be created in a 3-DAY time frame. Furthermore, 3-DAY molecular H2O and CO2 production and 6-DAY protein production are also possible if
then atomic hydrogen (both muonic-protons and electrons have been produced) can be created in a 3-DAY time frame. Furthermore, 3-DAY molecular H2O and CO2 production and 6-DAY protein production are also possible if
UH2O + UCO2 + Uprotein = ( 5.82 1053 + 8.35 1047 ) Joules.
This requirement would additionally therefore be the antecedent to further molecule production.
Conclusions
It has been shown in the present work that the distorted-space, or Distorted Geometry,” (DG), model of matter, can be configured as a “compound gravitational- and EM-energy based structural description of the Universe”, that is, geometrically distorted regions of the space time manifold can be realized to produce structures satisfying “Universe dimensions and energies” based on “energy conserving, time-based transition dynamics”. The dynamics of EM energy production is such as to convert an originally stable (but subsequently perturbed) EM-geometric-structure at UEM =Mass-Energy of UNIVERSE/2 =7.7(10)69 Joules into a muonic/electronic-building-block energy-distribution in one day. Earlier successful DG-modeling and mimicking of “Fermi-described beta decay” has been extended to mimically describe the Universe as a collapsing and exploding gravitational and EM energy-bearing entity.
Although not incorporated in the modeling, attributing an absorption coefficient, a material-quality, to the “gravitational-energy + EM-energy”, populated geometric-manifold can account for the observed inter-galactic EM-energy frequency shifts and should be considered as a responsible agent for said frequency shifts.
References
- Koehler DR. Geometric-distortions and physical structure modeling. Indi J Phys. 2013;87:1029-34.
- Riemann B. On the hypotheses which lie at the bases of geometry. Birkhauser. 2016.
- Tolman RC. Relativity, thermodynamics, and cosmology. Cour Corp. 1987;248.
- Schwarzschild K. On the Gravitational Field of a Point Mass according to the Einsteinian Theory. Astron Astrophys. Harvard University Press. 1979;31:451-55.
- Clifford WK. On the Space theory of matter. Proc Camb Philos Soc. 1976;2:295-96.
- Anderson PR, Brill DR. Evolving test fields in a black-hole geometry. Phys Rev.1997;55:468.
- Sones RA. Quantum geons. Arxiv. 2005.
- Koehler DR. Radiation-Absorption, Geometric-Distortion, and Physical-Structure Modeling. Trans Plasma Sci. 2017;45(12):3306-15.
- Herzfeld KF, Litovitz TA. Absorption and dispersion of ultrasonic waves. Acad Press. 2013.
- Herzfeld KF, Rice FO. Dispersion and absorption of high frequency sound waves. Phys Rev.1928;31(4):691.
- Alfven H. Cosmology: Myth or science?. J Astrophys Astron. 1984;5(1):79-98.
- Alfven H. On hierarchical cosmology. Astrophys Space Sci. 1983;89(2):313-24.
- Penzias AA, Wilson RW. A Measurement of Excess Antenna Temperature at 4080 Mc/s. Astrophys J Lett. 1965;142:419-21.
- Koehler D. The changing dynamics of a universe in transition. Adv Phys Sci. 2023;28(7):2350003.
- Koehler D. Black holes as geometric distortional extrema. Research square. 2022.
- Zibetti S, Rossi E, Gallazzi AR. On the maximum age resolution achievable through stellar population synthesis models. Mon Not R Astron Soc. 2024;528(2):2790-804.
- Fixsen DJ. The temperature of the cosmic microwave background. Astrophys J. 2009;707(2):916.
- Shemmer O, Netzer H, Maiolino R, et al. Near-Infrared Spectroscopy of High-Redshift Active Galactic Nuclei. I. A Metallicity-Accretion Rate Relationship. Astrophys J. 2004;614(2):547–57.
- Liu JR, Wang YL, Wang JM. Accretion-modified Stars in Accretion Disks of Active Galactic Nuclei: Observational Characteristics in Different Regions of the Disks. Arxiv. 2024.
- Watkins LL, Marel RP, Sohn ST, et al. Evidence for an intermediate-mass Milky Way from Gaia DR2 halo globular cluster motions. Astrophys J. 2019;873(2):118.
- Zloshchastiev KG. Spontaneous symmetry breaking and mass generation as built-in phenomena in logarithmic nonlinear quantum theory. Arxiv. 2011;42(2):261–92.
- Avdeenkov AV, Zloshchastiev KG. Quantum Bose liquids with logarithmic nonlinearity: Self-sustainability and emergence of spatial extent. J Phys Mol Opt Phys. 2011;44(19):195303.
- Zloshchastiev KG. Vacuum Cherenkov effect in logarithmic nonlinear quantum theory. Phys Lett A. 2011;375(24):2305-8.
Appendix
Mathematical foundation: Similar “static-modeling” was accomplished by Schwarzschild [SI-1] (also see Tolman [SI-2,p245] and see a Wikipedia entry [https://en.wikipedia.org/wiki/Schwarzschild_metric ]) which is quoted here in this regard: “In Einstein's theory of general relativity, the Schwarzschild metric (also known as the Schwarzschild solution) is an exact solution to the Einstein field equations that describes the gravitational field outside a spherical mass, on the assumption that the electric charge of the mass, angular momentum of the mass, and universal cosmological constant are all zero. The solution is a useful approximation for describing slowly rotating astronomical objects such as many stars and planets, including Earth and the Sun. It was found by Karl Schwarzschild in 1916, and around the same time independently by Johannes Droste, who published his much more complete and modern-looking discussion only four months after Schwarzschild.
According to Birkhoff's theorem, the Schwarzschild metric is the most general spherically symmetric vacuum solution of the Einstein field equations. A Schwarzschild black hole or static black hole is a black hole that has neither electric charge nor angular momentum. A Schwarzschild black hole is described by the Schwarzschild metric, and cannot be distinguished from any other Schwarzschild black hole except by its mass.”
The present geometric description of matter (mass-energy) successfully mimics the classical-physics Electromagnetic (EM) and gravitational-field models at large radii of the distorted (warped) region, or energetic-matter region, but the distorted-geometry-regional equations (a description of these same classical forces) depart significantly from Newtonian 1/r4 behavior at small radii (an infinity at r = 0) and thereby produce a magnetic-field (spin) matter-mimic as well as a weak-field matter-mimic (beta decay and the Fermi-constant, a force-constant which describes the magnitude of the strength of the weak fields); a strong-field mimic is also mathematically-manifest without an infinity at the origin. There are no infinities or singularities, which are the undesirable hallmarks of pure classical Newtonian and electromagnetic physical models of matter, in these presently, geometrically-constructed, structural models [SI-3].
Classically, physical forces have been characterized as independent entities, each with an associated strength (force constant), a Newtonian gravitational-force, an electromagnetic (electric and magnetic-force), a weak-force describing the physical phenomenon of beta-decay and a strong-force describing short-range-repulsion effects. These forces are all manifested in the mathematical attributes (force-characteristics or force-constants) of this ONE distorted-geometric form (the solution to the Riemannian geometric tensor equations 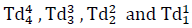 that is, the “metric-solution”,
that is, the “metric-solution”,
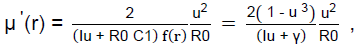
where R0 is a “distortion-describing” radius and 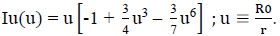 The geodesic equation for this spherically-symmetric geometry is
The geodesic equation for this spherically-symmetric geometry is
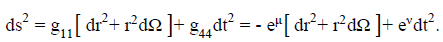
The “metric-solution” μ’ is further expressed fundamentally in the tensor energy-density (pressure) elements [(Fd14)2, (Fdmag)2, (Fdcore)2]
The μ’ “metric solution” satisfies the “Minkowski” requirement that the “Metric-element coefficient-functions must be consistent with Tμν = 0 (empty spacetime in the vicinity of a source mass) and must approach 1 as r approaches infinity, to become the Minkowski metric in spherical coordinates (the metric should be asymptotic flat.)” This present “distorted geometry” “metric solution” satisfies the Minkowski requirement that
μ ‘(r) = 0 at r = ∞ ,
and also intrinsically satisfies the condition that
μ ‘(r) = 0 at r = 0 ,
Therefore no infinities (dictated by the tensor energy-densities).
This “particular form” of the metric quantity μ’(r) is the solution to the actual metric equation (SI-6d) generated by the “Maxwellian-like” and “material-like” tensor relationship expressed in equation (SI-4):
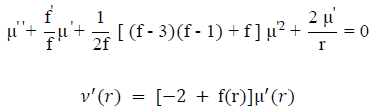
Equation (SI-6a)) and u ≡ R0/r. It should be understood that this equation is the fundamental, constraining or restricting and defining differential equation for the metric entity μ’(r) . The metric is not arbitrarily defined, it must satisfy this differential equation in the context of, and as dictated by, the Riemannian geometric equations (SI-4) and (SI-5). The inclusion of an “equation of state” as an additional “necessary or constraining” descriptor of “the distorted space,” in conjunction with the four Riemann tensor energy-density equations, produces the metric-defining differential equation (SI-6d).
The geometrically-warped structure is constituted by a core-region within which the propagation-velocity, by virtue of the distorted-region metrics, is greater than c and exhibits a “partial light trapping phenomenon,” facilitating and duplicating “black hole” behavior. Warping or distorting our spatial-manifold requires energy but with limits as to the degree of distortion thereby predicting and describing fundamental-electromagnetic-particle structures as well as gravitational (dark-matter, black-hole) structures.
For the presently described spherically symmetric Riemannian-geometric tensors, the Maxwellian electromagnetic tensor and the associated field tensor F1μ can be constructed according to equation (SI-1), where the only surviving field tensor components are (following the symbolism and development of Tolman [SI-2]):
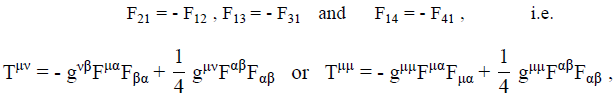
then
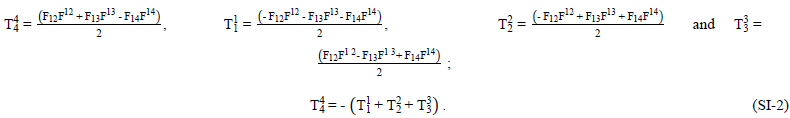
The resultant field quantities are
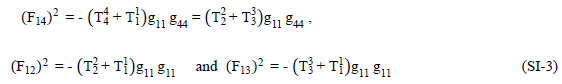
Therefore, we see that the static-spherically-symmetric Maxwellian tensors, (SI-1) and (SI-2), exhibit the same stress and energy relationship as the “equation-of-state geometric-tensors [SI-3],
The present geometric-modeling endeavor, with its Maxwellian-tensor-form mimicking-component, has produced the fundamental and limiting agent for the currently-studied distorted geometry, namely a particular constraining functional relationship between the geometry-defining tensors (for an empty-space geometry, all of the components of the energy-momentum tensor are zero). In characterizing this simple equation (SI-4) as an “equation-of-state” and as a restricting distortional-model tensor relationship, we thereby elicit the metric-defining differential equations for such a family of geometric distortions.
We constrain the modeling therefore by requiring that the descriptive stress-energy tensors satisfy this “constitutive relation” or “equation-of-state” between the temporal and spatial tensor-curvature elements, namely we require

We have introduced the explicit distortional-tensor symbolism Td for the geometric quantities. Contrast this perspective with cosmological renditions of geometric curvature structure resulting from “matter” causation, wherein several “equations of state” relating to the “matter” variables ρ (density) and p (pressure) have been forthcoming (SI-4) where p = σ ρ and where σ varies from -1 to +1.
Since, inherently, in the geometric “equation-of-state” constraint, the requirement that the descriptive stress-energy tensor, Td, be Maxwellian in nature requires that the mimicking process be limited to asymptotically flat-space regions of the manifold since 1/r2 field behavior does not adequately describe elementary-particle structural-detail.
The calculational treatment employs the isotropic coordinate description of equation (SI-1) and utilized by Tolman [SI-2], where the system of equations represented by equation (SI-1), is shown more explicitly in equation (SI-5) in mixed tensor form;
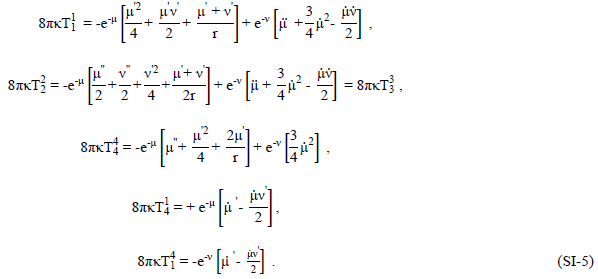
Metric coupling, that is terms such as μ’ν,’ are apparent in the fundamental curvature equations. The usual notation, where primes denote differentiation with respect to the radial coordinate r and dots denote differentiation with respect to the time coordinate t, is employed. We are considering the static case (where total differentiation replaces partial differentiation) as was also used for Schwarzschild’s (gravitational) interior and exterior solutions for the model of an incompressible perfect-fluid sphere of constant density surrounded by empty space [SI-1]. In that work a zero-pressure surface-condition and matching and normalization of the interior and exterior metrics at the sphere radius were used as boundary conditions.
Tolman [SI-2] has shown that the energy of a “quasi-static isolated system” can be expressed as “an integral extending only over the occupied space”, which we will allow to extend to infinity, and where the total energy of such a sphere is therefore expressed as
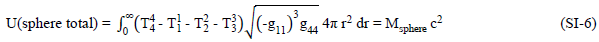
This mass-energy representation will be used throughout in calculating the distortional mass-energies. The distortional-tensor energy-density amplitudes manifested in these presently calculated geometric representations are both negative and positive, that is, there are both negative energy-density [SI-3] and positive energy-density regions internal to the distortions. Since geometric distortional fields arise from the same energy-density tensors, the negative energy-density geometric regions are also sources of negative energy-density field quantities.
Metric-element coefficient-functions must be consistent with Tμν=0 (empty spacetime in the vicinity of a source mass) and must approach 1 as r approaches infinity, to become the Minkowski metric in spherical coordinates (the metric should be asymptotic flat).”
The “Kerr” metric is an exact solution of the Einstein equations, generalizing the Schwarzschild metric to represent a “spinning black hole.”
The present functional construction can be compared with the Schwarzschild solution [SI-1] in isotropic coordinates where
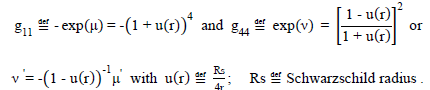
Equations (SI-5) can be written in a static system as
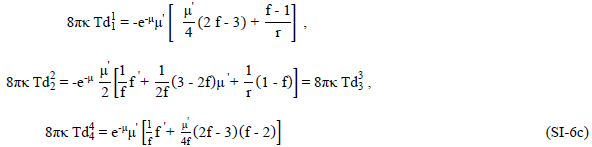
Imposing the “equation of state” relationship (SI-4), in the tensor Eq. (SI-6c) for Td44, the “metric differential equation” (SI-6d) is created.
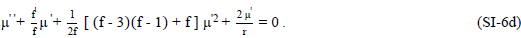
A solution to this equation (SI-6d) is found to be
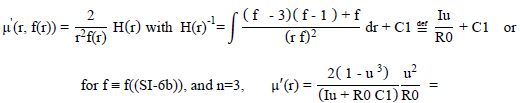

where
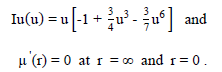
“For the special case where f = 1”, equation (SI-6d) becomes
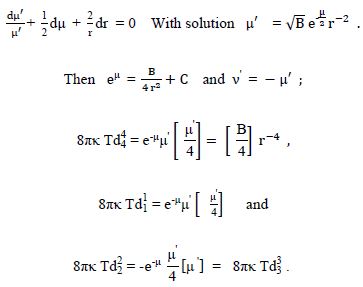
This “special case” is a description of a “Maxwellian Perfect-Fluid-like Distortion” with p0 (pressure) = ρ0 (mass-energy density); the definition of the “Maxwellian Perfect-Fluid” being - 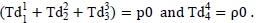 In this case, however, the metric-variables μ’, ν’ and the energy-density tensor quantities
In this case, however, the metric-variables μ’, ν’ and the energy-density tensor quantities 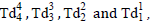 are all infinite at r = 0.
are all infinite at r = 0.
The μ’ metric solution satisfies the “Minkowski” requirement that the “Metric-element coefficient-functions must be consistent with Tμν=0 (empty spacetime in the vicinity of a source mass) and must approach 1 as r approaches infinity, to become the Minkowski metric in spherical coordinates (the metric should be asymptotic flat).” Moreover the μ’ metric solution, μ’(r) also satisfies the heretofore unsatisfied requirement that μ’(r = 0) = 0 for no infinities.
The metric quantities g44 and g11 behave consistently with the classical notion of a “Lorentzian-Riemannian smooth manifold with a continuous two-index metric tensor field, non-degenerate at each point of the manifold, which is a basic ingredient of general relativity and other metric theories of gravity”[SI-1].
Both mass and field equations are dominated by the μ’ function, but the radial region near the geometric origin requires a precise functional description of the metric quantities g44 and g11 to accurately characterize the fundamental physical quantities. In fact, as will be shown, the mass-energy quantity is exclusively generated by the transition region from “flat-space” to “distorted-space.”
Written in the “u” variable form,
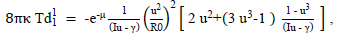
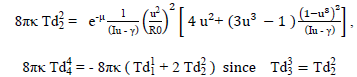
or
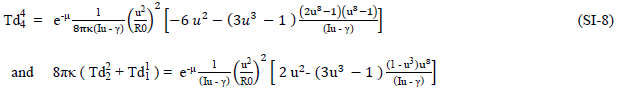
leading to
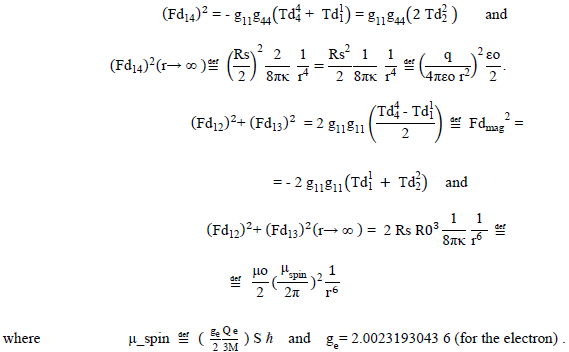
To illustrate the dependence of the tensor quantities on the metric quantity “near the radial origin,” we can show that for “non-infinite” behavior, n must be ≥3 ; for example,
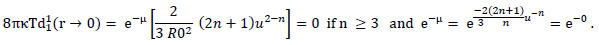
After solving for μ and subsequently forming the asymptotic metric form, that is, the expanded large-radius metric, we have equated the distortional-geometric form to a Schwarzschild form with the result that 2/C1 = -Rs. See for comparison the Reisner [SI-5] and Nordstrom [SI-6] metric form constructed in the standard coordinate system for an object with mass “m” and charge “e”.
Having constrained the first order large-r (or r→∞) metric behavior to the Schwarzschild value 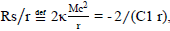 we have ascribed to the model the geometrically generated characteristic of “mass-energy” via an undetermined “microscopic geometrostatic coupling-factor”, κ. In this characterization, C1 must also be negative to satisfy the “pseudo-magnetostatic” field constraint elaborated below. Incorporation of the
we have ascribed to the model the geometrically generated characteristic of “mass-energy” via an undetermined “microscopic geometrostatic coupling-factor”, κ. In this characterization, C1 must also be negative to satisfy the “pseudo-magnetostatic” field constraint elaborated below. Incorporation of the 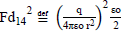 term (q is the charge quantity and εo is the permittivity constant) implies an inclusion of the geometrically generated characteristic of “electrostatic charge-energy” in the model (also see Tolman [SI-1]).
term (q is the charge quantity and εo is the permittivity constant) implies an inclusion of the geometrically generated characteristic of “electrostatic charge-energy” in the model (also see Tolman [SI-1]).
Because of the fundamental geometrostatic equation-of-state relationship, the 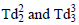 tensor elements are considered constructs of the basis tensors
tensor elements are considered constructs of the basis tensors 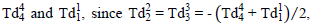 and therefore not basis elements themselves. Also for the geometrostatic case, the Fd122 and Fd132 field quantities are identical and therefore considered functionally addable, at the tensor expression level, to form the single field quantity Fdmag2. Although there are no “moving” charges in this static spherically symmetric model, the geometric field tensor entity (Fdmag)2 is non-zero and therefore both “pseudo-electrostatic” and “pseudo-magnetostatic” distortional fields are produced. The “pseudo-magnetostatic” distortional-field source-strength is that of a “magnetic-dipole of magnitude to produce the dipole-axial-field.”
and therefore not basis elements themselves. Also for the geometrostatic case, the Fd122 and Fd132 field quantities are identical and therefore considered functionally addable, at the tensor expression level, to form the single field quantity Fdmag2. Although there are no “moving” charges in this static spherically symmetric model, the geometric field tensor entity (Fdmag)2 is non-zero and therefore both “pseudo-electrostatic” and “pseudo-magnetostatic” distortional fields are produced. The “pseudo-magnetostatic” distortional-field source-strength is that of a “magnetic-dipole of magnitude to produce the dipole-axial-field.”
The electrostatic and magnetostatic constraints (where h = Planck’s constant q = particle electric-charge, M = particle mass, μo = permeability constant and c = speed of light ≡ the flat-space propagation-velocity within the geometric manifold), constructed at large radii with r-4 and r-6 behaviors, have therefore produced (or required for mimicking), in conjunction with the “metric mass-energy” constraint, that the coupling constant be a variable, 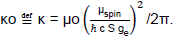 Having mimicked both mass-energy and electromagnetic-energy behavior, the coupling constant is a function of both source entities, the electric charge, and the mass, but in a combined fashion expressed through the single physical descriptor “μ_spin.” These constraints have also determined the geometrostatic quantities, R0 (the distortional-characteristic radius), and C1 (the metric-derivative integration constant). The results are summarized in equation (SI-9); κ, C1 and R0 have been expressed to show more explicitly the charge q and mass M dependence. The three geometric descriptors have been fixed by the two physical descriptors since C1 = C1(κ,M) and R0 = R0(κ,M).
Having mimicked both mass-energy and electromagnetic-energy behavior, the coupling constant is a function of both source entities, the electric charge, and the mass, but in a combined fashion expressed through the single physical descriptor “μ_spin.” These constraints have also determined the geometrostatic quantities, R0 (the distortional-characteristic radius), and C1 (the metric-derivative integration constant). The results are summarized in equation (SI-9); κ, C1 and R0 have been expressed to show more explicitly the charge q and mass M dependence. The three geometric descriptors have been fixed by the two physical descriptors since C1 = C1(κ,M) and R0 = R0(κ,M).
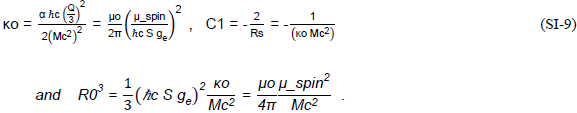
A structural-constant is manifested in the 1st mass-moment, R0 Mc2, or
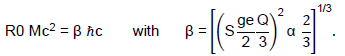
Although a classical presentation would not require a “quantization” restriction, we have included this feature to reflect the theoretically used quark concept.
Finally, the geometrostatic sphere “mass-energy” equation must be satisfied for internal integrity and modeling success.
By using the “equation-of-state” relationship for the geometric tensors, the mass equation integrand becomes 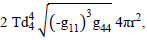 a function of the single geometric tensor element
a function of the single geometric tensor element 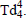 Writing the tensor component explicitly, we have for the “sphere mass energy,” a product of tensor energy-density and the distortional differential volume element.
Writing the tensor component explicitly, we have for the “sphere mass energy,” a product of tensor energy-density and the distortional differential volume element.
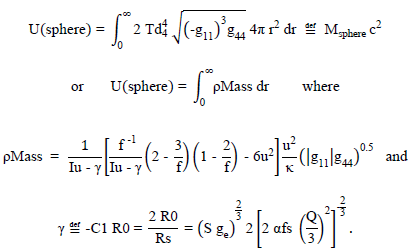
One can express the mass-energy integral in “normalized coordinates;”
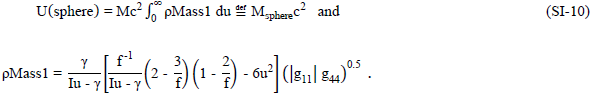
Then it is seen that the integral must evaluate to unity for equality. Expressing the mass energy-density in this fashion incorporates the effect of the distorted volume on the mass-energy’s radial dependence. The sphere-distortion energy is thus seen to be a function of “charge energy” through the integration constant γ and to “spin-energy” through the coupling constant κ.
One comprehensively describes such a geometric distortion family therefore by mimicking a physical “mass” quantity and a “spin” quantity, the “charge” quantity being subsumed in the former “spin” quantity. This should arise from the “two-basis-tensor” geometric foundation. The “mass-energy” quantity is further satisfied internal to the model in the geometrostatic tensor construct of equation (SI-6). In summary, equations (SI-4) through (SI-9) form the equation set for describing the distortional family’s “particle-like” characteristics and its associated Maxwellian-like fields. Classically and geometrically, any mass quantity is allowed and describable. Since the distortional description itself yields a constrained value for the geometrostatic coupling constant, we see that at the mass and charge levels considered here, larger values than the gravitational coupling constant are involved. It is to be noted that the gravitational coupling constant, G/c4, is approximately 37−42 orders of magnitude smaller than these geometrostatic Maxwellian-mimicked coupling-constant values.
Gravitational Field Energy density(units of Joules/meter3,
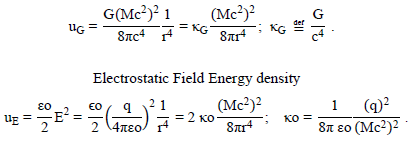
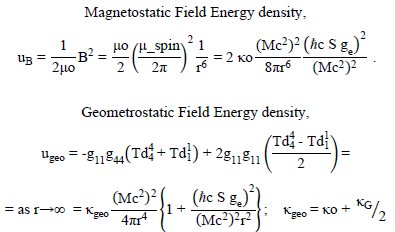
The field equations, in both the EM realm and the gravitational realm (Q = 0), exhibit r-6 geometric behavior which we have interpreted as constituting a “magnetic monopole” mimic (what is a “magnetic monopole” ?).
A 2-dimensional plot of this structure (T44 ( r ) for muon)) is included here to help visualize the “distorted-geometry” model FIG. 9.
Figure 9: SI-1 Mass-Energy-Density distribution-function surface-plots (two views) (linear radii and logarithmic amplitudes) for the geometric hole distortion.
References
[SI-1] Schwarzschild K. On the gravitational field of a mass point according to Einstein's theory. Arxiv. 1999.
[SI-2] Tolman RC. Relativity, thermodynamics, and cosmology. Courier Corporation; 1987.
[SI-3] Koehler DR. Geometric-distortions and physical structure modeling. Indian J Phys. 2013;87:1029-34.
[SI-4] E.V. Linder. First Principles of Cosmology. Addison Wesley: Essex England.1997;23.
[SI-5] H. Reisner, Static charged perfect fluid spheres in general relativity, Ann. Phys., (1916), 59 p.106.
[SI-6] Nordström G. On the energy of the gravitation field in Einstein’s theory. Koninklijke Nederlandse Akademie van Wetenschappen Proceedings Series B Phys Sci. 1918;20:1238-45.