Mini Review

, Volume: 11( 6) DOI: 10.37532/2320-6756.2023.11(6).349

• View PDF
• Download PDF

Three-Dimensional Venn Diagram as an Explanation of Two Kinds of Generality in Science, Invention, & Engineering

*Correspondence:

Christopher Portosa Stevens Dept. of Academic Affairs, University of Virginia Charlottesville VA 22904, USA, E-mail: acceleration207@gmail.com

Abstract

This paper describes a Venn Diagram with three dimensions, “Predictability,” “Generality,” and “Technological Growth”: this Venn Diagram is used to explain two kinds of generality in science, invention, and engineering instead of one kind: there is an additional kind of generality related to technological productivity and technological growth, like the technological growth related to the work of Alan Turing, Nicholas Metropolis, or Claude Shannon, in addition to generality related to the generality of predictions of some subject matter, like Ptolemy's predictive astronomy, or Copernicus' predictive astronomy, or Galileo's classical mechanics. The paper includes a provocative thought experiment on the nature of technology and biotechnology: Vico and Marx likely viewed the vast array of functional and adaptive capacities of plant and animal life as considerably greater than the technologies and inventions of human labor; in the 19th century biological adaptations of organisms, or what Vico and Marx called “natural technologies,” were unquestionably far greater than the technological adaptations of human labor and inventiveness; however, given the nature of technological growth, it may be possible for the vast array of human inventions to eclipse the number and diversity of “inventions” or functional and adaptive properties distributed across plant and animal life.

Keywords

Venn Diagrams; Generality; Predictability; Technological growth; Adaptation; Exponential growth

Introduction

Prominent philosophers of science Karl Hempel and Karl Popper developed ideal standards for evaluating generality and predictability of scientific theories and scientific discoveries (1-2): By the standards of Karl Hempel’s celebrated “Covering Law” model of scientific explanation, and Karl Popper’s celebrated if sometimes controversial “Hypothetico-Deductivism,” Arthur Eddington, in his famous test of Albert Einstein’s theory of general relativity, showed that Einstein’s theory of gravity and spacetime was more general than Galileo’s theory of gravity (and its applications in classical mechanics and early experimental physics) and more general than Isaac Newton’s theory of gravity uniting the movement of celestial bodies with explanations of the movement of objects at or near the surface of the earth.

However, from the standpoint of a Standard of Technological Productivity or Standard of Technological Growth, since Galileo’s theory and framework for gravity, classical mechanics, and the self-conscious manipulation of the forces of physics in experimental physics and invention directly or indirectly generated more inventions, technologies, and feats of engineering (such as in the industrial revolutions of Britain, France, and the United States in the 18th and 19th centuries) than Einstein’s theory, or, similarly, because Newton’s Laws for gravity, classical mechanics, and the self-conscious manipulation of the forces of physics directly or indirectly generated more inventions, technologies, and feats of engineering than Einstein’s theories, Galileo’s work and Isaac Newton’s work are more general than Einstein’s for technological productivity or technological growth.

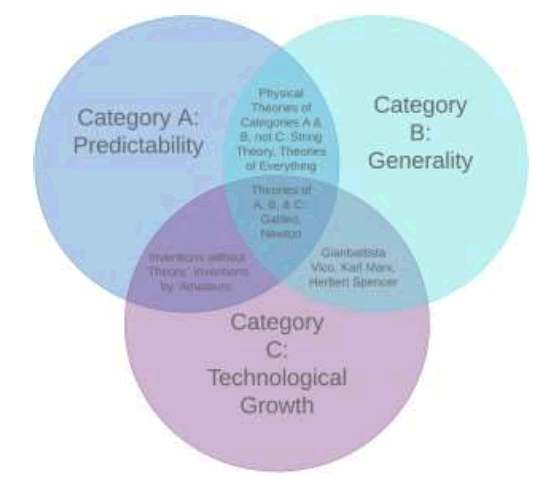
Thus, it is also possible to discern and distinguish different kinds of generality in science, technology, and engineering. This is represented in a Venn diagram classifying theories and frameworks in science by their capacity for prediction or predictability, their generality or scope, and their relationship to technological growth (FIG.1).

\

As suggested, Arthur Eddington showed in his test of Einstein’s theory of gravity space-time versus Newton’s theory of gravity, that Einstein’s theory of gravity was more general than Newton’s (and, thus, also more general than Galileo’s theory of gravity). However, if one were to classify different theories and frameworks in science by their capacity to directly or indirectly generate inventions, technologies, feats of engineering, and industrial and post-industrial revolutions, Galileo’s work has had a greater capacity for generating technological growth than Einstein’s, and Newton’s work has had a greater capacity for generating technological growth than Einstein’s; thus, while classic ideal models and theories of science and scientific explanation focus on generality in science in terms of predictability and testability, it is possible to recognize explicitly that there are two kinds of generality in science, technology, invention, and engineering: there is the generality of scientific theories, such as Galileo’s, Newton’s, or Einstein’s, that enjoy the highest levels of generality and predictability; however, though Einstein’s theory of gravity space time is highly general, and more general in scope than Galileo’s or Newton’s theories of gravity, there are different kinds of theories and models that may enjoy more generality than Einstein’s general theory of gravity space-time in terms of their capacity or relationship to the direction of invention, industrial revolutions, post-industrial revolutions, and technological growth.

Examples include Alan Turing and Nicholas Metropolis developing abstract models of computing machines for scientists and engineers to build computers, including before the physical components were available to build the computers, and suggesting different physical components that might be functionally interchangeable for the computers; Claude Shannon’s development of information theory for computer science and the digitization of sound, knowledge, and information when analog communications was still largely dominant (in 1956, The Soviet Academy of Sciences called Shannon’s ‘mathematical theory’ a theory of technology instead of mathematics); additional examples might include Michael Faraday’s conception of “force fields,” important for advances in physics, technology and engineering related to electromagnetism; Dmitri Mendeleev’s Periodic Table, important for inventions and advances in inorganic and organic chemistry, including metals, alloys, semiconductors, pharmaceutical products and medicines; Ben Franklin’s theory of the conduction of electricity, tested in his famous kite experiments.

Thus, this Venn Diagram is used to identify and explain two kinds of generality in science, technology, engineering, and invention instead of one kind: that is, there is an additional kind of generality in science related to technological productivity and technological growth, like the technological growth related to the work of Alan Turing, Nicholas Metropolis, or Claude Shannon, in addition to generality related to the generality of predictions of some subject matter, like Ptolemy's predictive astronomy, or Copernicus' predictive astronomy, or Galileo's classical mechanics.

Materials and Methods

Theory: Galileo’s and Newton’s theories fit or include all three categories (“Theories of Categories A, B & C,” from FIG. 1); however, String Theory and “Theories of Everything” in physics include the first two categories but not all three categories, Predictability, Generality, and Technological Growth. String Theory, while potentially highly general, has been criticized by many physicists, scientists, and philosophers of science for not having any explicitly empirical or testable results: String theory has been described as a “potential unified theory of nature string theory not only reconciles quantum mechanics and gravity, but can also contain within it electrons, protons, photons, and all the other observed particles and forces, and hence is a viable candidate for a complete unified theory of nature” [3]. However, the American Physical Society comments that, “String theory has not yet made any testable predictions, and some scientists’ worry that string theorists have strayed too far from physical reality in their obsession with mathematics” [4]. Nobel prize-winning physicist Sheldon Glashow has similarly commented that String Theory has not made “even one teeny-tiny experimental prediction.”

Mathematical physicist Peter Woit, formerly a participant in String Theory, has evaluated the oeuvre of String Theory as “not even wrong,” in his book Not Even Wrong: The Failure of String Theory and the Search for Unity in Physical Law [5]. (In this, Woit uses Wolfgang Pauli’s famous characterization of theories in physics that are testable and wrong as more valuable than theories that are untestable). Woit argues that String theory is not empirically testable, is “post-empiricist” from the standpoint of empirical science, and argues that String Theory has failed in its attempts to unify the forces of physics or to successfully attach String Theory to particle physics. The Venn diagram in this paper dramatizes another criticism of String Theory and “theories of everything”: there are no important inventions, technologies, feats of engineering, or industrial or post-industrial revolutions that are explicitly derivable or at least related to the Theory of String Theory.

Results and Discussion

The Venn diagram has spaces for inventions and innovations that might include Predictability and Technological Growth, though not Scientific Generality per se, as in inventions, manufacturing processes, and industrial products that may occur without explicit use of theoretical science, including inventions and manufacturing processes by so-called “amateurs”; in the history of the industrial revolutions of 18th and 19th century Britain, France, and the United States, inventions, industrial processes, and industrial products were sometimes generated or invented without explicit use of scientific theory: physicists such as Jearl Walker or computer scientists such as John Graham-Cumming have shown that it was not until years later that physicists might attempt to employ physical theories to explain why particular inventions “worked,” or the success of many inventions, manufacturing processes, and industrial products [6, 7].

There has been a consensus of contemporary 20th and 21st century physicists and astronomers to simplify the number of forces in the physical sciences to gravity-spacetime, electromagnetism, and the strong and weak forces (thus discarding additional concepts of forces used in earlier Galilean and Newtonian physics, or 18th and 19th century physics related to the Industrial Revolution). In practice, however, engineers, inventors, and technologists use more than the four forces of gravity-spacetime, electromagnetism, and the strong and weak forces when they create, invent, and manipulate technologies in the physical sciences. Moreover, inventors sometimes invent tools, technologies, and manufacturing processes that do not make reference to the established knowledge of physical theory (and that intuitively make use of more than the four forces of physics stipulated by contemporary theoretical physicists): when scientists analyze the nature of inventions that are not explicit applications of physical theory, they sometimes invoke more than the four forces of physics stipulated by contemporary theoretical physicists.

Thus, for example, computer scientist and inventor John Graham-Cumming writes that, “In 1782, William Watts patented a method of making lead shot that involved pouring molten lead through a copper sieve and letting it fall a long distance before being cooled in a pool of water. Watts was less concerned with the science than with the result. But if he asked, “How does this work?” the answers would have covered surface tension, intramolecular forces, and terminal velocity.” Graham-Cumming also explains the nature of Watts invention with gravity and upward drag: “How fast is the lead shot going when it hits the water?

Gravity is acting on the falling body, but this is balanced by the drag from the air. Bodies falling through the air experience an upward force caused by drag, which is proportional to the square of their velocity. The force is defined by the equation F = -½ CpAv².” Other physicists and engineers, such as Jearl Walker, when they analyze and seek to explain why specific technologies work, or the basis of complex interactions of “everyday” physical phenomena, use more than four forces in their explanations. By point of comparison, String Theory is not used by physicists, inventors, or engineers to develop or invent important technologies, inventions, feats of engineering, or generate industrial revolutions or post-industrial revolutions.

Another space in the Venn diagram is for theories and frameworks that may demonstrate considerable generality, and inspire or are related to technological growth, though may be lacking in predictability. Are there any examples? What are the examples? Examples may include Gianbattista Vico and Karl Marx’s classification scheme and analogies for identifying, categorizing, and distinguishing the vast array of functional and adaptive capacities of plant and animal life as “natural technologies”; Vico and Marx likely viewed the vast array of functional and adaptive capacities of plant and animal life as considerably greater than the technologies and inventions of human societies or “artificial technologies” or artifices; their framework also was a way of inspiring greater innovation and inventiveness in societies as the vast array of “natural technologies” provided analogical models for human generated inventions and technologies. This section thus includes a thought experiment on the nature of technology and biotechnology: in the 19th century, biological adaptations of organisms, or what Vico and Marx called “natural technologies” were unquestionably far greater than the technological adaptations or artifices or “artificial technologies” of human labor, inventiveness, and societal productiveness; however, given the nature of technological growth, and the recognition that technology grows exponentially (or that at least some technologies grow exponentially) by figures such as G.E. Moore (“Moore’s Law”), or earlier figures that wrote on exponential technological growth, such as Henry Adams and William Ogburn, it may be possible for the vast array of human inventions, manufacturing processes, industrial and post-industrial revolutions to eclipse the number and diversity of “inventions” or functional and adaptive properties and adaptive structures distributed across plant and animal life.

(Admittedly, this would be difficult to measure, i.e., attempting to measure the number and diversity of biological adaptations and adaptive properties and structures across all biological species, and then attempting to compare the number and diversity of functional inventions and tools of human labor and inventiveness; this framework also may assume a disjunct or separation between human generated technology and plant and animal adaptive characteristics as classified by Vico and Marx, and also implied by Darwin’s principle of gradualism as applied to the evolution of animal and plant species; it is as if the growth of physical technologies and biotechnologies create the capacity for invading or re-organizing the “natural technologies” of animal and plant species, potentially undermining the classic physical and conceptual divide between the functional capacities of the “natural technologies” of the adaptive properties of plant and animal species, and the functional capacities of human generated or “artificial technologies” that might invade or re-organize the adaptive properties of animal and plant species for ill, or for worse, or for superior organisms, or for increasing the rate of evolution against Darwin’s principle of gradualism, or, counter-intuitively, for undermining the rate of evolution and thereby undermining fundamental Darwinistic processes; the separation between human generated technologies and plant and animal adaptive properties or “natural technologies” has been collapsing for several decades with the potential introduction of different techniques for bio-technology and genetic engineering); it is an interesting question what other theories or models might fit in the logical space of the intersection of Generality and Technological Growth without Predictability per se: possibly the systems of Herbert Spencer (social Darwinism) and Auguste Comte (scientific socialism), with their elaborate classification schemes related to considerable scientific and technological advances in Britain and France in the 19th century; Spencer and Comte’s schemes also may have stimulated or helped generate technological advances in their societies, and also other European societies and the United States, by organizing knowledge in the sciences and relating it to advances and developments in human social organization; however, sometimes Spencer and Comte attempt predictive models in early political economy and the intersection of physics, biological science, and early social science, though with mixed success (at least some of their work, especially their elaborate classification schemes of scientific knowledge and human social organization fit the logical space of the intersection of the categories of Generality and Technological Growth without explicit Predictability).

Conclusion

The discussion involves four categories at the intersections of the Venn Diagram: “Theories of A, B, & C,” i.e., Galileo’s and Newton’s theories; “Theories of Categories A & B, not C,” i.e., String Theory and Theories of Everything: “Inventions without Theory or by ‘amateurs,’” i.e., inventions that do not involve the explicit or self-conscious use of general theories or theoretical science, including inventions by amateurs; “Generality and Technological Growth, without Predictability,” i.e., theories and frameworks that stimulate and relate to technological growth without explicit predictive models, i.e., the frameworks of Gianbattista Vico, Karl Marx, Auguste Comte, or Herbert Spencer.

(In principle, instead of only focusing on the four categories at the intersections of the Venn Diagram, there are seven categories of the Venn Diagram, including Predictability, Generality, and Technological Growth; however, given the nature of the phenomena in question, science, theory, technology, invention, and engineering, there might be only isolated cases of in early science and technology of theories, discoveries, or inventions that only have predictability without generality or technological growth, or cases of philosophical speculation, metaphysics, and theology, like the intermediate stage in Comte’s Law of Three Stages, that might have generality without predictability or technological growth; the cumulation of technological growth is perhaps the most common pattern across societies before the development of general and predictive scientific explanations, such as by the frameworks of Galileo or Newton, that might be used to self-consciously manipulate the forces of nature for invention and engineering).

Thus, this three dimensional Venn Diagram, with its four categories at the intersection of its three dimensions, is useful to identify, discern, and explain two kinds of generality in science, technology, invention, and engineering: that is, while classic ideal models and theories of science and scientific explanation focus on generality in science in terms of predictability and testability, it is possible to explicitly re-organize and re-classify knowledge in science, technology, invention, and engineering to recognize that there are two kinds of generality in science, technology, invention, and engineering: the generality of scientific theories, such as Galileo’s, Newton’s, or Einstein’s, that enjoy the highest levels of generality and predictability, and the generality of theories and models of Galileo’s, Newton’s, Faraday’s, or Franklin’s, that may be less general than Einstein’s or James Clerk Maxwell’s in terms of generality of predictive science, though more general in terms of their relationship to the direction of invention, industrial revolutions, post-industrial revolutions, and technological growth.

Acknowledgements

I thank the reviewers for their comments.

Conflict of Interest

The author declares no conflict of interest.

REFERENCES

1. Hempel CG. Two basic types of scientific explanation. Philos. Sci.: Cent. Issues. 1962:685-94.

   [Google Scholar] [Crossref]

2. Popper K. Logic of Scientific Discovery. New York: Free Press. 1960 [Google Scholar] [Crossref]
3. National Academy of Sciences. “Andrew Strominger, National Academy of Sciences.” . 2019 [Google Scholar] [Crossref]
4. American Physical Society. Einstein’s Quest for a Unified Theory.  2005 [Google Scholar] [Crossref]
5. Woit P. Not even wrong: The failure of string theory and the search for unity in physical law. Basic Books (AZ); 2006.

   [Google Scholar] [Crossref]

6. Walker J. The flying circus of physics. John Wiley Sons; 2006.

   [Google Scholar] Crossref]

7. Graham-Cumming J. The Geek Atlas: 128 places where science and technology come alive. " O'Reilly Media, Inc."; 2009

   [Google Scholar] [Crossref]