Review

, Volume: 7( 3) DOI: 10.37532/2320-6756.2019.7(3).184

• View PDF
• Download PDF

The Long Arc of Light and Gravity

*Correspondence:

Greg Poole, Industrial Tests, Inc. Rocklin, CA, USA, E-Mail: greg@indtest.com

Abstract

The nature of light and gravity is explored in this exciting new frontier of cosmic electrodynamics. The light gravity equivalence formula 𝑔 = 𝑐2 𝑟 proves electro-radiation to be the driving force of gravity. Like Isaac Newton’s cannonball, photon torpedoes are represented as projectiles launched from Earth, which produce flight times, have a launch angle and travel incredible light year distances. Altitudes are represented as deflections of light, or the long arc of light; a bending pattern which we know creates inward acceleration or (g). The Earth is again represented as a mass spectrometer to explain how its electromagnetic field bends particles and light to create gravity. Electromagnetic fields traveling at the speed of light radiate outward from the center of the Earth’s core. The Earth behaves as a rotating spherical antenna emanating a circular radiation pattern, extending all the way to a distance of a light year and beyond. Keywords

Keywords

Arc; Centripetal acceleration; Gravity; Mass spectrometer; Projectile motion; Speed of light

Introduction

In his book, Isaac Newton visualized cannon on top of a very high mountain [1]. If there were no forces of gravitation or air resistance, the cannonball fired by the cannon should follow a straight line away from Earth in the direction that it was fired. If a gravitational force acts on the cannonball, it will follow a different path depending on its initial velocity. If the speed is low, it will simply fall back on Earth. It starts moving up and forward, at some inclination to the ground. The further it flies, the slower the ascent is-and finally, it starts descending, moving now downwards and finally hitting the ground again. If you could trace its path, it would be a curve called a trajectory in the shape of a parabola. Any object moving in such a way is in projectile motion.

Instead of a cannon ball, we will perform an identical thought experiment replacing the slow-moving cannon ball with a high-speed photon torpedo. A photon torpedo will behave in the same manner even though it is traveling at the speed of light. Only one force acts on a photon projectile-the electromagnetic field force-generated by the Earth’s electromagnetic and electrostatic field. Air resistance is omitted in our calculations as most of the distance that the photon travels through space is in a vacuum. In my diagram of the photon cannonade or light, I draw one downward vector and denote it “gravity”, which is simply a centripetal acceleration. If there was any other force acting on the body, then-by projectile motion definition-it would not be a projectile. Light is thus a stream of photon projectiles in motion; derived from electromagnetic radiation and bent by an electromagnetic force.

Projectile Motion Parameters

To calculate the standard parameters of projectile motion [2] the following must be taken into consideration:

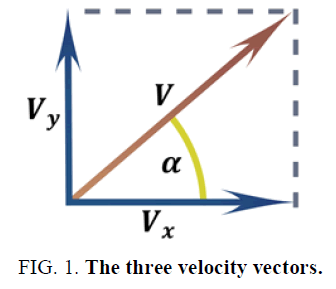
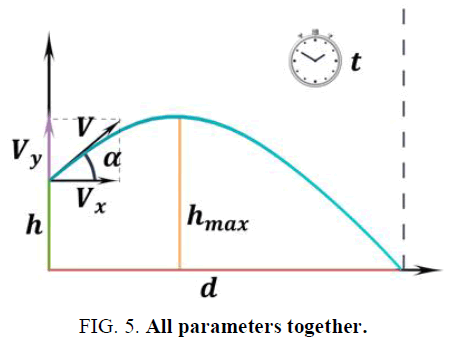
A. Calculate the components of velocity (FIG. 1)

• V is the total velocity

• α is the angle of launch

• V_x is the horizontal velocity component and is equal to Vcos(α)

• V_y is the vertical velocity component and is equal to Vsin(α)

• Three vectors -V, V_x and V_y- form a right triangle

If the vertical velocity component is equal to 0, then it is a case of horizontal projectile motion. If, additionally, α = 90° then the projectile will move vertically upwards at 90°.

B. The equations of motion

i. Distance:

• Horizontal distance traveled can be expressed as 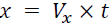, where t is the time

• Vertical distance from the ground is described by the formula 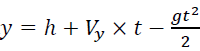, where g is the gravitational acceleration

ii. Velocity:

• Horizontal velocity is equal to V_x

• Vertical velocity can be expressed as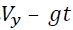

iii. Acceleration:

• Horizontal acceleration is equal to 0

• Vertical acceleration is equal to -g (because only gravity acts on the projectile)

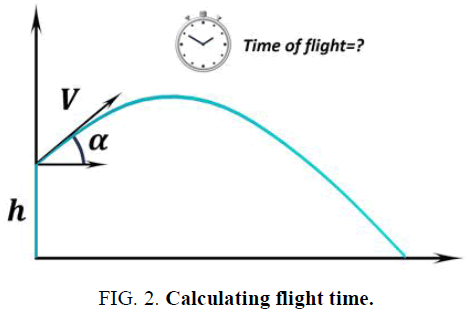
iv. Calculate the time of flight: Flight ends when the projectile hits the ground. This can also be described as the point when the vertical distance from the ground is equal to 0. In the case where initial height is 0, the formula can be written as: 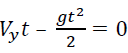. Then, from that equation, we find that the time of flight is (FIG. 2):

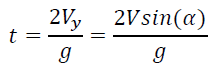
However, if we throw the object from some elevation (h), then the formula does not reduce as before, and we obtain a quadratic equation:

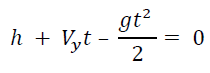
After solving this equation and we get:

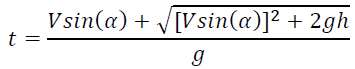
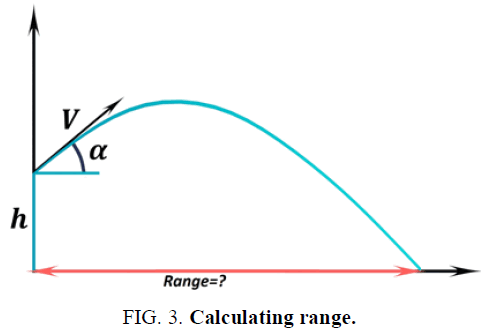
C. Calculate the range of the projectile

The range (R) of the projectile is the total horizontal distance traveled during the flight time. Again, if we launch the object from the ground (initial height=0), then we can write the formula as

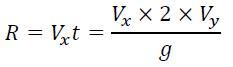
It may be also transformed into the form:

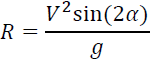
Things get more complicated if the initial elevation is not 0. Then, we need to substitute the long formula from the previous step with (FIG. 3):

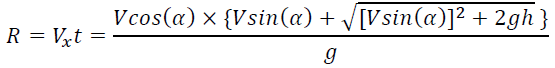
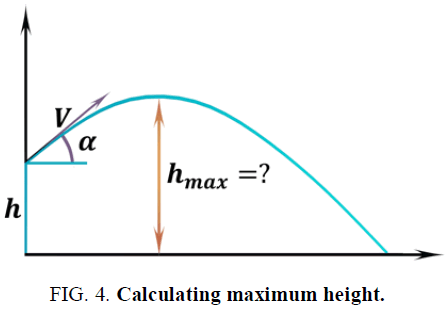
D. Calculate the maximum height (h_max) (FIG. 4)

When the projectile reaches the maximum height, it stops moving up and starts falling. It means that its vertical velocity component changes from positive to negative-in other words, it is equal to 0 for a brief moment in time t(V_y=0)

If 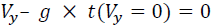, then we can reformulate this equation to:

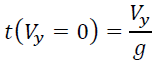
Now, we simply find the vertical distance from the ground at that time:

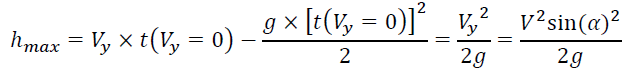
Fortunately, in the case of launching a projectile from some initial height h, we need to simply add that value into the final formula:

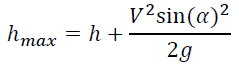
Inserting the speed of light into the various equations and assigning a hypothetical angle of the launch of 31 degrees, I obtain the time of a standard Julian light year and the distance of a light-year when adjusted for height or deflection (FIG. 5).

Velocity=3 × 10⁸ m/s

Angle of launch=31°

Initial height=0 m

Time of flight=3.15 × 107s

Distance (d)=8.1 × 1015 m

Maximum height=1.22 × 1015 m

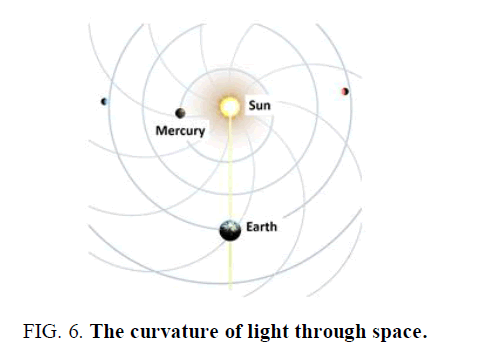
Traditionally we have thought light to be traveling in a straight line and calculate the distance of a light-year by 3e8 m/s × 3.15e7 seconds=9.45e15 meters. In this new model, we see that light bends and space is thus smaller. When I use a lunar time based on 354 days, I calculate a light year of 9.15e15 meters. If I set aside the debate of relative time or calendars and just imagine a large number of photons or particles breaking away from the Earth in a weakening electromagnetic field, we can visualize the curvature of light in space in the figure below (FIG. 6). These curvatures of light then create an inward acceleration from the constant velocity. The radius, or arc of light, is so long that it is not perceptible, and so gravity has been hidden for centuries behind a veil of light.

Planets as Mass Spectrometers

In my first paper, I proposed that the Earth acts as a mass spectrometer [3]. A mass spectrometer is a means of splitting up a source that contains a mixture of particles with different masses. These days it is often used to identify the molecular masses of compounds. The only difference between compounds is their atomic mass.

An electron or photon departing the Earth is accelerated through an electric field and deflected in a magnetic field.

The amount of deflection depends on the mass of the particle:

• Ions that have too big a mass are not deflected enough

• Ions that have too small a mass are deflected too much

• Ions that are slow are deflected more easily

• Ions that are traveling fast are not deflected as readily

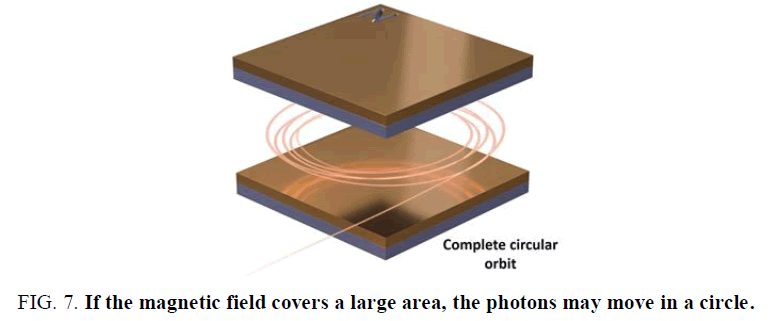
When electrons travel into a magnetic field they are deflected. A large magnetic field will increase the deflection. The force is the same force that deflects a wire carrying an electric current. The force is always at right angles to the motion of the electrons and has a size of F=B_qv (FIG. 7).

Where,

B=0.0005 Tesla, Earth’s magnetic field strength

q=1 × 10^-35 charge of γ radiation (photon) [4]

v=3 × 108 m/s, speed of photon particle

Sir JJ. Thomson used this technique to measure the specific charge of electrons [5]. He knew that the size of the force that acts on them is B × q × v. However, the size of the force that holds an object in a circular orbit is given by:

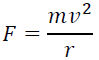
If the magnetic force is the only force available, then it must have a size equal to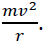

Therefore:

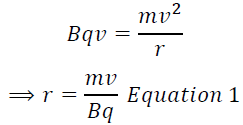
Also, when the electrons are accelerated, the electrical potential energy lost=kinetic energy gained.

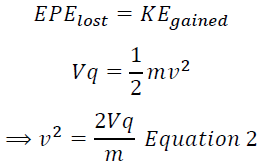
Squaring equation 1 gives us:

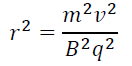
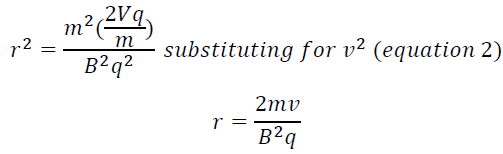
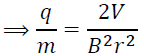
q/m is the specific charge of the electron. It is also known as the charge to mass ratio. Sir JJ. Thomson's cathode rays all followed the same path-i.e. the beam did not get split up. This meant that the particles in the beam must all have the same specific charge.

We can use the same principle with just about any charged particle. If the specific charge is constant, the beam will stay together. If it varies, then the beam will split up. This is the principle of the mass spectrometer. This is the nature of the Earth; the beam is split up at the poles and electrons of varying specific charge are fired in a circular path at various distances around the globe, as near as the surface of the Earth and as far away as a lunar light year. The Earth is thought to be scattering particle waves into space as it is spinning around its axis.

We can now see how a star’s or a planet’s electromagnetic variable affect the radius of the arc. The various variables that affect this include:

A. Charge

Effect: Changing the sign of the charge will deflect a particle in the opposite way.

Rationale: For a beam of positive particles, the current is going in the same direction as their velocity. For a beam of negative charges, the current is in the opposite direction. Using Fleming's left-hand motor rule, we can work out that the force on a particle beam will reverse if the charge is reversed.

B. Mass of particle (constant speed)

Effect: More massive particles will have a reduced deflection.

Rationale: The force on the particles will be the same. However, their bigger mass (inertia) will mean that their sideways acceleration is less for lighter particles- they travel in a larger arc.

C. Increasing the speed

Effect: The faster particles will be deflected less.

Rationale: The radius of the circular orbit increases as the velocity increases. So faster particles are deflected less.

D. Mass of particles (constant energy)

Effect: More massive particles will still have a reduced deflection.

Rationale: It is useful to consider this because the energy given to a particle depends on the accelerating voltage. For a constant voltage, the more massive particle will travel in a larger arc-i.e. they will not be deflected so much. We can show that the radius of the arc is given by:

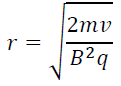
This shows that, for a fixed voltage, a bigger mass leads to a larger radius.

In this paper, we can also begin to discern the nature of the speed of light. From 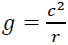we can conclude that

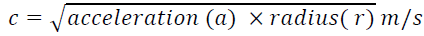
Acceleration is the rate of change of velocity, or the derivative of velocity. The nature of the speed of light (c) is thus the square root of the cross product of acceleration and distance. The speed of the electron or light varies as a function of acceleration and radius. In order for the Earth’s gravity to remain a constant 9.8 m/s², the speed of the electron, or the speed of light must have an extremely long arc or vary speed accordingly. Electron particles are thought to be traveling at variable speeds closer to the surface of the Earth due to a constant acceleration of the Earth. However, the speedy photon travels a much flatter longer arc and achieves its maximum speed of light (3 × 108 m/s) at the Earth’s lunar light year. There may actually be a sphere of light circling the globe. What a magnificent expression of universal gravitation to think the Earth enveloped by the speed of light. Based on simple physics and intuition it would seem that light, from our perspective on Earth, travels in a relatively straight line and the arc of the universe is a truly long one to travel so fast and so far with just a slight inward acceleration to create gravity (g).

The Earth is an induction motor literally throwing out electrons of varying specific charge all the way to a lunar light-year (FIG. 8). Since it is a sphere with a decaying voltage (electrostatic) and magnetic field (electromagnetic) it is behaving like a mass spectrometer. The net effect of the bending velocity and radius (a=v²/r) is a constant acceleration inward or gravity.

Photons are thought to have very little mass, ≤ 1 × 10^-18 eV [4]. The maximum speed of light is determined by the lunar light-year, which is a function of relative time and the theoretical maximum speed of light.

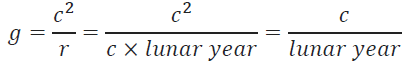
c=g × lunar year

c=g × (354 days × 86,400 s/day)

c=299,738,880 m/s

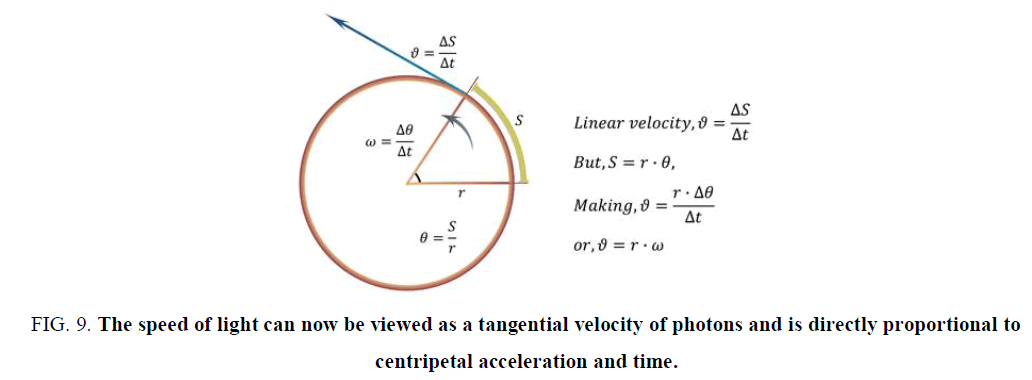
The speed of light can now be viewed as a tangential velocity of photons and is directly proportional to centripetal acceleration and time (FIG. 9).

It is thus concluded that there are a series of ever-growing circles of electrons generated by solar and planetary electromagnetic radiation (FIG. 10); culminating in very long arcs which fill the universe with electromagnetic waves traveling at the speed of light, or c.

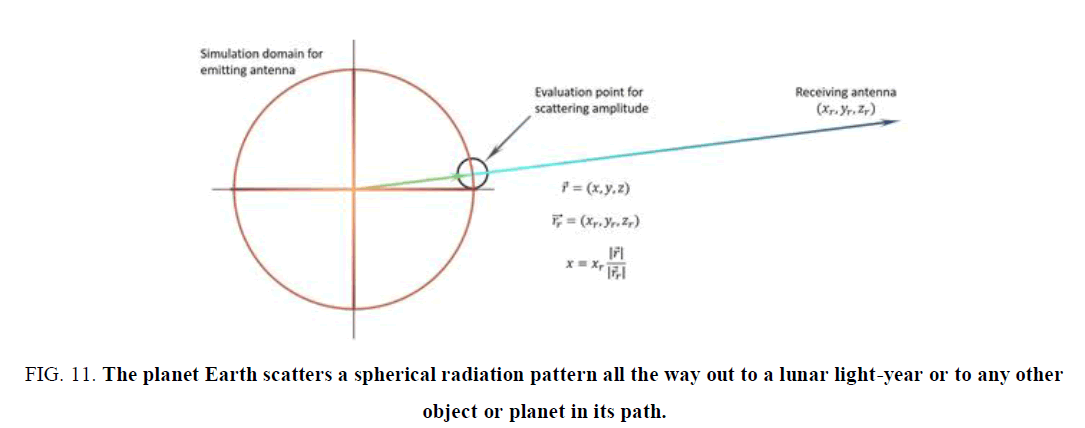
This then also confirms my paper on Cosmic Wireless Power Transfer and the Equation for Everything [6]. Suns and planets act as rotating spherical transmitters and receivers broadcasting a variety of wavelengths and frequencies. The planet Earth scatters a spherical radiation pattern all the way out to a lunar light-year or to any other object or planet in its path (FIG. 11).

Conclusion

I conclude that Issac Newton was correct about gravity using his cannonball thought experiment. Had he known of the existence of electrons and photons; Newton would have easily solved his own problem on gravity. Newton just missed meeting Benjamin Franklin, the “Newton of Electricity”, while Franklin was visiting London. Newton had no way of knowing that the invisible forces of voltage and current were bending particles and light. These forces create gravity and caused the cannonball to fall. Electromagnetism bends ions, particles, and electrons. Electromagnetism also bends light which was proven by Michael Faraday in 1845 [7]. Using our new equation 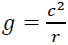, we can readily see that gravity is equivalent to c2, which results from electromagnetic radiation and the inverse of the radius. Gravity is thus a centripetal acceleration created by electromagnetic forces that bends particles similar to a mass spectrometer. Light is bent, which changes the distance of a light-year, as the crow (satellite) flies. However, the actual distance remains the same as doe’s time. Time and space for a spherical star or a planet’s electromagnetic field are somewhat dynamic but for human purposes relatively constant. However, we can conclude that fluctuations in stellar voltages and currents will impact the magnetic field and thus the bending force. It is expected that a light-year will have some variance due to cosmic power fluctuations. Space or the radius and size of a planetary electromagnetic sphere will then increase or decrease according to the length of a light-year. The bending of space is simply an increase or decrease in the size of the electromagnetic sphere. Gravity is directly proportional to the trajectory and speed of light and the strength of the stellar magnetic field. Further investigation and research in the field of cosmic electrodynamics are recommended.

I wish to close with the words of Minister Theodor Parker who wrote, “I do not pretend to understand the moral universe, the arc is a long one, my eye reaches but little ways. I cannot calculate the curve and complete the figure by the experience of sight; I can divine it by conscience. But from what I see I am sure it bends towards justice” [8].

Newton’s cannon ball was launched using his laws (a=v²/r) and has now returned from its orbit nearly 300 years later. To commemorate his great thought experiment, we imagine firing a modern photon torpedo using essentially the same law (g=c²/r). Will another 300 years lapse before students listen for the echo of the cannon? Will the noise of the photon torpedo draw them back to the achievements and advances made during Newtonian physics and impel them to learn from the true masters? Might we see a resurgence in classical physics and investment in experimentation? Might we see a return to the hard work of real science and testing done in the laboratory? Might we create anti-gravity machines for our space trek into the final frontier? Will research into cosmic electromagnetism lead us to resonant electromagnetic energy from the planet and space itself? Understanding the electromagnetic fields of the stars and the planets is the key to gravity, anti-gravity, and tapping the unlimited energy resources of the universe itself. We scientist must understand the magnetic field and map it out in detail. There is no greater opportunity to make an impact on society and the environment than to understand and harness the power of planetary electromagnetism.

Acknowledgement

The author wishes to acknowledge ASK Scientific (https://www.askscientific.com) for assistance in formatting and artwork. Also, a special note of love and devotion to my son, whose thoughts on black holes rotating faster than that the speed of light led me to seek the correlation between the speed of light and gravity.

References

1. https://www.christies.com/lotfinder/Lot/newton-sir-isaac-a-treatise-of-the-5331969-details.aspx
2. https://www.kopykitab.com/S-Chands-Principles-Of-Physics-For-XI-by-V-K-Mehta-And-Rohit-Mehta
3. Poole G. Theory of electromagnetism and gravity-modeling earth as a rotating solenoid coil. JHEPGC. 2017;3:663-92.
4. Amsler C. Review of particle Physics: Gauge and Higgs bosons. Phys Lett B. 2008;667:1-6.
5. https://todayinsci.com/T/Thomson_JJ/ThomsonJJ-CathodeRays(1897).htm
6. Poole G. Cosmic Wireless Power Transfer System and the Equation for Everything E=mc2=vc2/60=a3/T=G(M1+M2)/4π2=(KE+PE)/1.0E15=Q=PA/F=λ/hc=1/2q=VI=1/2LI2=1/2CV=I2R=. JHEPGC. 2018;4: 588-650.
7. http://faradaysdiary.com/ws3/faraday.pdf
8. https://archive.org/details/tensermonsofreli00inpark/page/n6