Opinion Review

, Volume: 12( 11)

• View PDF
• Download PDF

The Conservation Laws in Quantum Mechanics

*Correspondence:

Richard Oldani
Illinois Institute of Technology NY, USA
E-mail: oldanirl@gmail.com

Abstract

Although quantum mechanics correctly predicts what it is possible to observe (the emissions) it ignores the other half of natural phenomena, what cannot be observed (the absorptions), thereby violating the conservation laws. By describing only one-half of quantum mechanics conceptual difficulties such as wave function collapse, infinite paths, non-locality, and abstract mathematical models appear out of nowhere. The deficiencies are corrected in non-relativistic theory by showing that the unobserved absorption energies of off-diagonal elements in matrix mechanics are essential and that matrix and wave mechanics are equally important for formulating a complete quantum mechanics. Due to the conservation of energy absorption must be carried out to completion before energy emission can begin. When relativistically correct equations of motion are derived they show that the wave function is incomplete because it describes the excitation and decay of an electron with twice the allowable action minimum. Einstein’s unfinished quantum theory forms the mathematical foundation leading up to and underlying the proposed mathematical model.

Keywords

Conservation laws; Quantum mechanics; Hamilton’s principle; Energy; Momentum; Path integral formulation; Matrix mechanics

Introduction

It is often claimed, whether overtly or implied, that the most accurate theory is the best theory. A clock that was accurate to within one second over the age of the universe was later improved upon by a clock accurate to within 100 milliseconds. The most recent clock experiment can differentiate between gravitational potentials of one millimeter [1]. Clock accuracy is continuously being improved upon because it is believed that more accurate time measurement “offers new opportunities for tests of fundamental physics”. In another area of research universities are competing to improve upon measurements of the g-2 factor of an electron [2]. Once again, the goal is to find a discrepancy with the standard model that will lead to “new physics”. Improved instrumentation, more accurate measurements, and better predictions are the procedures that many say will lead to an improved understanding of Nature. We will show in these pages that improved accuracy does not equate with improved understanding, and that it is precisely what cannot be observed that is the key to understanding natural phenomena.

The importance of the observer, and by inference the observation, in scientific inquiry is a sticking point that has a long history in theoretical physics. On one side is Bohr and the majority of physicists. “It is wrong to think that the task of physics is to find out how nature is. Physics concerns what we can say about nature.” On the other side of the dispute, Einstein had this to say. “On principle, it is quite wrong to try founding a theory on observable magnitudes alone.”
Our purpose is to determine which of these two approaches is the more accurate, the empirical or the intuitive.

Momentum Conservation

Einstein’s theory

Einstein’s first attempt at a quantum theory was a derivation of Planck’s law by statistical methods “in an amazingly simple and general manner” [3]. There he describes the dynamic equilibrium that exists between the thermal energy absorbed by molecules and its subsequent quantum mechanical emission as black body radiation. Heat energy that is absorbed according to classically defined Maxwell Boltzmann statistics is transformed at the molecular level and emitted according to the Planck radiation law. The absorption of energy by a molecule leads to momentum +E/c in the direction of propagation, while the emission of a photon causes a recoil momentum -E/c that is directed in the opposite direction of propagation. The sudden reversals and random nature of the impulses cause molecular trajectories to be discontinuous, as observed in Brownian motion.

As is typical of Einstein’s work he begins his derivation at a fundamental level taking into consideration the conservation laws. “If a radiation beam with a well-defined direction does work on a Planck resonator [quantum oscillator], the corresponding energy is taken from the beam. According to the law of conservation of momentum, this energy transfer corresponds also to a momentum transfer from the beam to the resonator.” He demonstrates here the close association that exists between momentum and energy. Molecular impulses transfer energy to the oscillator which then radiates the energy when an electron decays. Thus, energy absorption is differentiated from energy emission. He continues, “Let a molecule of given kind be in uniform motion with speed v along the X-axis of the coordinate system K. We inquire about the momentum transferred on the average from the radiation to the molecule per unit time. To calculate this, we must consider the radiation from a coordinate system K′ that is at rest with respect to the given molecule. For we have formulated our hypotheses about emission and absorption only for molecules at rest.” The molecules in a gas absorb energy classically in K and emit energy quantum mechanically in K′. The absorbed energy must be equal to the emitted energy due to the conservation of energy. The emission and absorption of energy is to be described quantum mechanically in the coordinate system K′ which is “at rest with respect to the given molecule”, while the kinetic energy of molecules will be treated with “ordinary mechanics” in the coordinates of the system K. To determine the total energy of a molecule we sum a classical component due to kinetic energy, as determined by temperature; and a quantum mechanical component due to the energy of excited states.

The inclusion of both classical and quantum mechanical energy forms in the same model of radiation is a feature that distinguishes Einstein’s methods from all others [4]. It contrasts sharply with the Bohr-Heisenberg method, which derives two independent expressions, one classical and one quantum mechanical, and then links them by using the correspondence principle. The Schrödinger method links the quantum and classical worlds by means of wave function collapse, a process that introduces conceptual difficulties and violates special relativity theory. However, the quantum classical divide was never a problem for Einstein, for he accepted it as a fundamental property of matter. There are classical laws governing molecular behavior in K and quantum laws governing a molecule’s behavior in K′; two points of view of a single reality.

Heisenberg’s theory

Heisenberg formulated a theory of quantum mechanics that reconciles the continuity of radiation fields with the discrete energy states of an atom by expressing electron transitions in the form of a matrix [5].

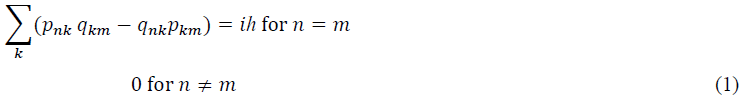
Although p in the above equation refers to momentum it is not the momentum of photon emission and absorption in K used by Einstein, rather it is the momentum of the electron in its orbital in K′. To compare (1) more closely with Einstein’s statistically defined measurements of energy fluctuation we refer to the Hamiltonian matrix [6]. The diagonal elements of the matrix m=n are believed to refer to all possible transition energies of a quantum system. Because the theory only concerns quantum mechanical phenomena it represents a complete break from classical theory. Its weakness lies in the fact that it does not include transition energies that cannot be observed, the absorption energies in K. In other words, equation (1) is formulated exclusively in coordinates relative to K′.

The spectroscopic properties of hydrogen are produced by heating hydrogen gas to create an emission spectrum. The transfer of heat to a gas has been extensively studied and occurs due to both classical and quantum mechanical means. It initiates with classical exchanges of energy in K by the temperature dependent motion of particles, which may also be described by infinitesimal changes in state by means of the quantum electron Hamiltonian equation, ?=-?2/2m∇2 +V(r), which is composed of kinetic and potential energy terms. To describe the heat absorption of a hydrogen gas molecule we begin with matrix elements, or electron transitions, far from the diagonal, gradually proceeding closer to the diagonal as the temperature increases. Electron transitions can be either positive or negative so the complete matrix of an atom requires a two-fold infinite number of elements to describe all possible energy exchanges, with energy emission occurring when electrons have net positive transition energies. In other words, energy must first be absorbed before electron decay can occur and cause spectroscopic phenomena to be generated and observed. No one has ever used matrix mechanics to study the function of an atomic oscillator, for if all off-diagonal matrix elements are equal to zero the atom would be immersed in a “thermal bath” equal to absolute zero and would not radiate at all.

Feynman’s theory

In the path integral approach to quantum mechanics we can see violations of the conservation laws even more clearly. In the following passage Feynman considers absorption and emission by using the field approach of quantum field theory [7]. “If one solves the problem of an atom being perturbed by a potential varying sinusoidally with time, which would be the situation if matter were quantum mechanical and light classical, one finds indeed that it will in all probability eject an electron whose energy shows an increase of hν, where ν is the frequency of variation of the potential. When, however, we come to spontaneous emission and the mechanism of the production of light, we come much nearer to the real reason for the apparent necessity of photons. The fact that an atom emits spontaneously at all is impossible to explain by the simple picture given above.” By deriving a theory of spontaneous emission that does not specify how energy is absorbed he obtains extremely accurate predictions, but at the expense of physical consistency. Spurious infinities associated with the self-energy of an electron must be artificially subtracted away by means of “renormalization” in order to make meaningful calculations and accurate predictions. Failure to recognize the need for absorption energy results in particle paths unbounded both in geometry, by curved and looping trajectories, and spatially, by paths that exceed the energy of excited states and can even extend to infinity. Both are clear violations of the conservation laws and of special relativity theory. To correct the deficiencies we introduce a relativistic theory of the absorption and emission of radiation.

Relativistic Quantum Mechanics

Energy absorption

A theory of quantum mechanics compatible with special relativity is sought after by describing emission and absorption with the time integral of a Lagrangian and applying the calculus of variation [7]. Consider a radiating atom with ground state |1> and excited state | 2>. To describe the electron’s equation of motion during energy absorption we make use of Hamilton’s principle function S = ∫Ldt ,where L=T-V. It provides for a more economical expression of the laws of motion by specifying fixed boundary conditions for particle paths rather than trajectories in the Cartesian coordinates of Newton’s laws. The limitations of absolute space and time inherent to Newton’s laws are thereby avoided.

Due to the conservation of energy, absorption must occur before emission is possible. Quantization by a continuous absorption of energy is not amenable to a description by a purely field model because the fields are not bounded. Instead, we use a particle model and describe the electron during continuous excitation between the states |1> and |2>. The Lagrangian for the electron is equal to the kinetic energy T minus the potential energy V, or L=T-V. The transition of an electron from the ground state to an excited state is characterized in generalized coordinates with six dimensions, three to describe its position on the electron shells R1 and R2, and three to describe its trajectory.

The electron initiates its motion at a point on the equipotential surface R₁ of the ground state at time t₁, is excited along a path r, and upon arriving at R₂ after a period of time, (t₂ – t₁) = τ. It then assumes the experimentally determined orbital angular momentum, (T-V) = 2πE. The action, S[r(t)], is a functional that describes the absorption process in four dimensions. It has as its argument an infinite number of functions, the possible electron trajectories r(t). When we evaluate the action integral for a quantum mechanical change of state, we obtain the familiar Bohr relation describing a photon,

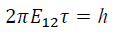
and simplifying, we have E₁₂ τ = ?, which is equivalent to the more familiar time-averaged relation E=hν.

Energy emission

At the relativistic or high end of the energy spectrum in quantum field theory, particles are treated as excited states of the more fundamental underlying quantum fields. As Nobel laureate Frank Wilczek noted, "In quantum field theory, the primary elements of reality are not individual particles, but underlying fields” [8]. On the other hand, when we examine lower energy interactions in nonrelativistic theory, we find that interpretations are almost exclusively about particles. It seems that theoreticians use fields when it is convenient to use fields, and particles when it is convenient to use particles. However, the physical principles that underlie mathematical models demand consistency. In quantum field theory the equations of motion are determined by minimizing the Lagrangian in a region of space-time. We will follow these same practices in order to extend the field interpretation to nonrelativistic theory.

The region of space-time that is of interest for lower energy interactions lies between the two states of an electron transition. Therefore, we specify a field boundary coincident with the atom’s excited state, an electron shell, that acts to localize particles and fields inside the atomic space. Within the space-time region we define a Lagrangian density of the fields and their first derivatives £(?i, ?i,μ) which allows for a complete accounting of the energy interactions, where ?i is the current density and ?i,μ is the electromagnetic field strength. The action integral for a quantum oscillator with an outer electron that occupies either of two allowable energy states may now be formulated in a way that is consistent with special relativity theory. Changes in action are evaluated by integrating the Lagrangian density four-dimensionally thereby yielding a relativistic formulation of emission that is invariant, the same for all observers.

The end points of the electron’s path are located on an equipotential, space-like surfaces, and the four-dimensional localization of the fields necessarily corresponds to the reduced Planck’s constant ? arrived at from (2). The action S[?i(t)] is a functional, a function of the values of coordinates on the discrete boundaries of the space-time surfaces R₂ and R₁ which are in turn functions of the continuous space-time variables of the fields within the surface. The change in action yields a relativistic formulation of emission that is invariant, the same for all observers. The action S[?i(t)] is a functional, a function of the values of coordinates on the discrete boundaries of the space-time surfaces R₂ and R₁ which are in turn functions of the continuous space-time variables of the fields within the surface. The field boundaries are uniquely fixed in four-dimensions by the volume ∫d³x and the time interval t₂-t₁ causing photon emission to be described as a four-dimensional localization of fields.

Comparison of the relativistic and non-relativistic models

The overriding problem in quantum mechanics has been how to describe two physical processes, absorption and emission, with a single equation. According to the Schrödinger wave equation they occur as a single process that evolves symmetrically in time. The wave function ψ used to describe an electron oscillating between two energy states performs two complete rotations, or a total of 720 degrees, before returning to its original state. If the electron is represented mathematically by a vector in Hilbert space |ψ> then one rotation of 2π results in a negative value -|ψ> and a second rotation of 2π brings the electron back to its original state |ψ>. The rotation occurs in abstract space so no physical interpretation is possible.

Our model, uses an action functional to describe quantization in real space and real time. A four-dimensional absorption of energy by the electron is followed by a four-dimensional localization of field and release of a photon. We interpret the first rotation of the wave function not as a rotation in abstract space, but as the change in phase of electromagnetic fields from 0 to 2π during energy absorption in real space. Thus one “rotation” of the wave function is interpreted as one full cycle of an electromagnetic wave and an increase in the electron’s energy from the ground state to an excited state. The second rotation occurs as the electron returns to the ground state and is interpreted as a localization of electromagnetic field energy and emission of a photon. The dual wave-particle nature of the photon is thereby realized in a physical transformation. The external appearances of a radiating atomic system, the frequency and intensity of its spectral lines, are observables described by the matrix mechanical formulation in (1), where the Hamiltonian matrix includes both absorption and emission processes for all possible radiation processes. Due to the conservation of energy no observable can be realized unless absorption and emission are both present.

A test to determine which physical model is correct, the relativistic Lagrangian model or the non-relativistic Hamiltonian model, has been proposed. It concerns differing physical interpretations for neutrino flavor oscillation as outlined in a paper on galactic structure [9].

Discussion

When quantum mechanics first appeared in 1926 it was questioned why two formulations, matrix mechanics and wave mechanics, were necessary. Mathematical equivalence was demonstrated by showing that the matrix mechanically determined energy states of the Bohr atom and the eigenvalues of wave mechanics define the same physical endpoint. However, every other aspect of the models; their experiments, mathematical formalisms, and physical interpretations; is different. The two theories both describe the same invariant physical observables that characterize the steady states, but they do not explain why they follow different paths to arrive there. Einstein’s unfinished theory answers that question by showing that radiation processes occur in two physically independent steps, absorption in K and emission in K′ [3]. We adopt Einstein’s mathematical convention describing the foundations of quantum theory in the remainder of this paper. Thus two coordinate systems and two distinct mathematical formulations exist; matrix mechanics originating in K and ending with the eigenvalues, and wave mechanics which originates in K′ and produces the eigenvalues. Both physical processes are needed for a complete quantum mechanics, and due to the conservation of energy the first (absorption) must be carried out to completion before the second one (emission) can begin.

Conclusion

We propose a formulation of quantum mechanics that is mathematically complete and visualizable. The matrix mechanical model describes how energy is absorbed by a quantum system, and the wave mechanical model, describes how energy is emitted. Absorption is described with the continuously superposed electromagnetic fields of Maxwell’s equations together with discrete contributions from off-diagonal matrix elements, while emission is described relativistically with both discrete and continuous coordinates as in equation (3), or non-relativistically with the Schrödinger wave equation. The transition between the two mathematical formulations requires switching from a set of classical “base states“ in K, which are the states of definite linear momentum and the z-component of angular momentum, to the state vector |?? in K′. The state vector |?? can be represented as a linear combination with suitable coefficients of a set of basis vectors, or as a superposition of unit vectors. We describe the transition from classical base states to quantum mechanical unit vectors as a physical transformation that connects the energy transition described by equation (2) with that described by equation (3).

To illustrate the classical/quantum discontinuity we consider the atomic process of parametric down conversion, where the impact of a photon on a non-linear crystal produces two photons with perpendicular polarization. The photons are created in the coordinate system K′, at rest with respect to atomic structure. Subsequently they follow different trajectories in accordance with the conservation of energy and momentum as defined in K. There is nothing unusual about the entanglement that exists between the two photons because it is the result of a physical transformation that occurs after the photons’ origin in K′ at t₁ and before their propagation in K at t₂. Wave function collapse, when the polarization of both photons becomes known, is the sudden recuperation of coordinates in K that were suppressed when the wave function was formulated.

References

1. Bothwell T, Kennedy CJ, Aeppli A, et al. Resolving the gravitational redshift across a millimetre-scale atomic sample. Nat. 2022 ;602(7897):420-4.

   [Google Scholar] [Crossref]

2. Guellati-Khelifa. Searching for New Physics with the Electron’s Magnetic Moment. Physics. 2023;16:22.

   [Google Scholar] [Crossref]

3. A Einstein. Quantum theory of radiation. 1917.

   [Google Scholar] [Crossref]

4. Oldani R. Einstein’s revolutionary ideas. Qeios. (2024).

   [Crossref]

5. Heisenberg W. Quantum-theoretical re-interpretation of kinematic and mechanical relations. Z. Phys. 1925;33:879-93.

   [Google Scholar] [Crossref]

6. Feynman RP. Feynman Lectures on Physics: Electrical and Magnetic Behavior. Perseus Books. 1999.

   [Google Scholar] [Crossref]

7. Feynman RP, Brown LM. Feynman's thesis: a new approach to quantum theory. World Sci. 2005.

   [Google Scholar] [Crossref]

8. Oldani R. Galactic Symmetry. Preprint. 2024. 8.

   [Crossref]

9. Wilczek F. Mass without mass I: Most of matter. Phys Today. 1999;52(11):11-3.

   [Google Scholar] [Crossref]

10. Oldani R. Galactic Symmetry. Preprint. 2024. 19.

    [Crossref]

11. Van der Waerden BL. From matrix mechanics and wave mechanics to unified quantum mechanics. In The physicist’s conception of nature. Dordr: Springer Neth.

    [Google Scholar] [Crossref]