Original Article

, Volume: 12( 2)

• View PDF
• Download PDF

The Alternative Formulation of Van't Hoff Equation

*Correspondence:

Irfan H Lone , Department of Chemistry, Government Degree College, Kupwara-193222, Kashmir, India, Tel: 7051248200; E-mail: lone.irfan3@gmail.com

Abstract

An alternative formulation (named total entropy equation) of Van't Hoff's equation has been presented. An explanation of the effect of temperature on exothermic and endothermic processes is provided in terms of this alternative formulation. The treatment can be useful in directly highlighting the central role that the total entropy change plays in determining the direction of the process. As a chemical example the calculations of total entropy change are presented for the Haber-Bosch process. Finally, the correlation between Van't Hoff's equation and Total entropy equation is demonstrated by showing that it is possible to derive the former from the later and vice versa.

Keywords

Van't Hoff equation; Entropy; Exothermic; Endothermic; Gibbs-Helmholtz equation

Introduction

The Van’t Hoff equation 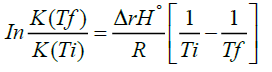[1]:

(1)

is usually derived [2-6] by making use of the Van’t Hoff isotherm:

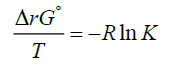(2)

and the Gibbs-Helmholtz [7-9] equation:

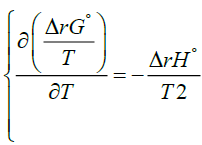(3)

 

More specifically, to obtain equation (1) one substitutes equation (2) for Δ_rG° into the left-hand side of equation (3) and integrates. The Van’t Hoff equation is used to know the variation of an equilibrium constant K with temperature [2,3]. This effect of temperature on the equilibrium constant is usually understood through its effect on the standard Gibbs energy of reaction Δ_rG° [10,11]. The standard state of a substance refers to 1 bar pressure. In other words, any change in K with T is perceived as a change in the value of the standard Gibbs energy of reaction Δ_rG° [3]. Furthermore, the dependence of K on temperature is determined by the sign of Δ_rH° and the Van’t Hoff equation provides the theoretical basis of this dependence [12]. Alternatively, the effect of temperature on equillibria has sometimes correctly, but only qualitatively, been explained in terms of the relative importance of the magnitudes of the entropy changes of the system and its immediate surroundings [2]. This is done by employing the following relation:

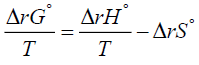(4)

In order to provide a mathematical expression corresponding to this alternative explanation the Van’t Hoff equation may be formulated in terms of entropy. This we do in the following sections. The presented equation, it is hoped, is a useful expression that highlights in a more direct manner the role that total entropy change (System+Surroundings) plays in the process.

The Equation

If one multiplies both sides of equation (4) by the negative sign, one gets

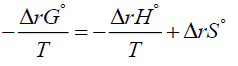
If one identifies the first term on the right hand side of above equation with the entropy change of the surroundings [13] and denotes it by 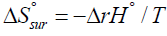then, since 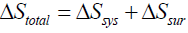, one finds [14]:

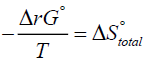(5)

Here ΔS°_total is the total entropy change that the reaction generates and T denotes the absolute temperature. ΔS_total is sometimes also called ΔS_universe or ΔS_isolated but we won’t use such designations here. For us the universe will consist of the system and its immediate surroundings as is usually the case in a typical chemistry laboratory. Although equation (5) does give some indication of the role that ΔS°_total plays in determining the favourable path of a process, it is useful to appreciate the role of ΔS°_total fully. If instead of equation (2) one substitutes equation (5) into the left hand side of equation (3) one obtains:

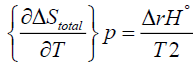(6)

Equation (6) can be directly integrated between the two specified temperatures T_i and T_f, say, to give the following general result:

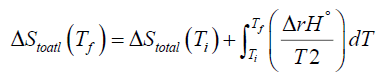(7)

Here T_i is the initial temperature while T_f is the final temperature. In order to carry out above integration further one must know how the enthalpy of the system varies with the temperature [15-18]. If one uses the approximation that the standard reaction enthalpy is independent of temperature, a valid approximation for at least small ranges of temperature [2], then equation (7) can be easily integrated to give the following special result:

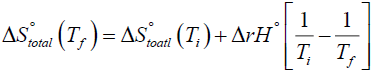(8)

Equations (7) and (8) represent an alternative formulation of Van't Hoff's equation in terms of entropy.

 

Results and Discussion

Equation (8) is an important result as it can be used to explain the behavior of exothermic and endothermic processes towards temperature directly. According to equation (8), for exothermic processes (the processes that are accompanied by the evolution of energy as heat as the reactants get converted to products) the increase of temperature leads to a net decrease in total entropy. Hence the equilibrium constant for an exothermic process decreases with increase of temperature as can be easily seen from a comparison of equations (2) and (5). On the other hand, a decrease in temperature leads to a net increase in total entropy and the equilibrium constant increases, also obvious from a comparison of (2) and (5). This must be so because ΔrH°<0 for an exothermic system. Now if we apply equation (8) to endothermic processes (the processes that are accompanied by the absorption of energy as heat as the reactants get converted to products) we find that the increase of temperature leads to a net increase in total entropy. Hence for endothermic processes the equilibrium constant increases with increase in temperature. On the other hand decrease in temperature leads to a net decrease in total entropy and K_eq decreases with a decrease in temperature, again obvious from a comparison of equations (2) and (5). This must be so because Δ_rH°>0 for an endothermic system.

An Application: The Haber-Bosch Process

The Haber-Bosch process named after its inventors, the German chemists Fritz Haber and Carl Bosch, who developed it in the first half of the 20th century [19], is an artificial nitrogen fixation process and is the main industrial procedure for the production of ammonia today [20]. This important process consumes over one percent of humanity's energy production but is responsible for feeding roughly one-third of its population and has been of somewhat greater fundamental importance to the modern world than the invention of the airplane, nuclear energy, space flight, or television [21]. The Haber-Bosch process is an exothermic process that converts atmospheric nitrogen (N₂) to ammonia (NH₃) by reaction with hydrogen (H₂) using a metal catalyst under high temperature and pressure and is usually depicted by the following chemical equation:

N₂(g)+3H₂(g) ≡ 2NH₃(g)

Now for the Haber-Bosch equilibrium process the value of Δ_rH°=-92.2 KJmol^-1 at 298 K and the value of K_eq is then 6.1 × 105. Suppose the value of Δ_rH° is independent of temperature up to about 500°C and the temperature is increased above room temperature in steps of 50°C. One can then calculate the variation of ΔS°_total with temperature by using equation (8). These values of ΔS°_total at different temperatures above room temperature [with ΔS°_total=110.40 JK^-1mol^-1 at 298 K, available from the already existing chemical literature, for example see reference-2 or calculated by using equation (5)] are shown in table below.

As is clear from above Table 1, ΔS° _totaldecreases as T increases for the above Haber-Bosch exothermic process. This means that the process becomes unfavourable at higher temperatures.

Table 1: Values of ?S°total at different temperatures for the Haber-Bosch process.

The Correlation between Van't Hoff Equation and Total Entropy Equation

Now using equation (8) one can easily obtain the Van't Hoff equation or Van't Hoff's law. If one uses equation (5) one can also write (8) as

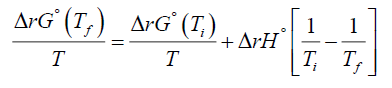(9)

Now one substitutes equation (2) into equation (9) to get the desired result

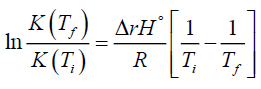(10)

Alternatively, if one takes equation (10) and works backwards by using equation (2) in it one gets the total entropy equation,equation (8).

Conclusion

An alternative thermodynamic interpretation of the behavior of exothermic and endothermic processes towards temperature is in terms of the total entropy change that the process causes. It is possible to present a mathematical expression, named as the total entropy equation, underlying this explanation. The presented equation makes it very direct to appreciate the role of total entropy change in the processes.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be considered as a potential conflict of interest.

Acknowledgements

The author would like to thank Prof. Carl O. Trindle (University of Virginia) for many useful suggestions for the improvement of the article.

References

1. Van’t Hoff JH. Die Rolle des osmotischenDruckes in der AnalogiezwischenLo?sungen und Gasen. Z Physik Chem. 1887;1:481-93.
2. Atkins PW, De Paula. J Physical Chemistry,10thed.Oxford University Press, UK. 2014:255-7.
3. Atkins PW, De Paula. JElements of Physical Chemistry, 4thed.Oxford University Press, UK. 2005:170-2.
4. SilbeyRJ, AlbertyRA, Bavendi MG. Physical Chemistry, 4th ed.John-Wiley and Sons Inc. UK. 2005:145-8.
5. EngelT, Reid P. Physical Chemistry. Pearson Education, Inc. 2006:131-3.
6. McQuarrieDA, Simon JD. Physical Chemistry, University Science Books, Sausalito, CA, USA. 1997:977-81.
7. Gibbs JW. Transactions of the Connecticut Academy of Arts and Sciences, New Haven. 1875;3:108-248.
8. Gibbs JW. Transactions of the Connecticut Academy of Arts and Sciences, New Haven. 1877;3:343-524.
9. Helmholtz HV. Die Thermodynamic ChemischerVorgange. 1882;93-101.
10. GlasserL. Correct use of Helmholtz and Gibbs function differences, ΔA and ΔG: The Van’t Hoff reaction box. J Chem Educ.2016;93(5):978-80.