Original Article

, Volume: 15( 4)

• View PDF
• Download PDF

Structure of M (I): Ternary Gamma-Semigroups

*Correspondence:

Madhusudhana Rao D, Associate Professor, Department of Mathematics, VSR & NVR college, Tenali, Guntut (Dt), Andhra Pradesh, India, Tel: 9440358718; E-mail: dmrmaths@gmail.com

Abstract

The terms, ‘I-dominant’, ‘left I-divisor’, ‘right I-divisor’, ‘I-divisor’ elements, ‘M (I)-ternary Γ-semigroup’ for a ternary Γ-ideal I of a ternary Γ-semigroup are introduced and we characterized M (I)-ternary gamma semigroups.

Keywords

Completely prime ternary Γ -ideal; I-dominant element; I-dominant ternary Γ-ideal; I-divisor; M (I)-ternary Γ -semigroup

Introduction

In [1] introduced the concepts of A-potent elements, A-divisor elements and N (A)-semigroups for a given ideal A in a semigroup and characterized N (A)-semigroups for a pseudo symmetric ideal A. He proved that if M is a maximal ideal containing a pseudo symmetric ideal A, then either M contains all A-dominant elements or M is trivial. In this paper we extent these notions and results to M (I)-ternary Γ-semigroups.

Experimental

Preliminaries

Definition 2.1: Let T and Γ be two non-empty set. Then T is said to be a Ternary Γ-semigroup if there exist a mapping from T × Γ × T × Γ × T to T which maps (x₁,α,x₂,β,x₃) → [x₁αx₂βx₃] satisfying the condition: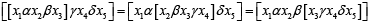 ∀ x_i ∈ T 1≤ i ≤ 5 and α,β,γ,δ∈Γ. A nonempty subset A of a ternary Γ-semigroup T is said to be ternary Γ-ideal of T if b,c∈T, α,β∈Γ, a∈A implies bαcβa∈ A,bαaβc∈ A,aαbβc∈ A. A is said to be a completely prime Γ-ideal of T provided x, y, z ∈ T and xΓyΓz ⊆A implies either x∈ A or y∈A or z∈ A. and A is said to be a prime Γ-ideal of T provided X,Y,Z are Ternary Γ-ideal of T and XΓYΓZ⊆A⇒X⊆A or Z⊆A. A ternary Γ-ideal A of a ternary Γ-semigroup T is said to be a completely semiprime Γ-ideal provided 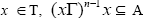for some odd natural number n>1 implies 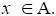Similarly, A ternary Γ-ideal A of a ternary Γ-semigroup T is said to be semiprime ternary Γ-ideal provided X is a ternary Γ- ideal of T and 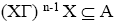for some odd natural number n implies X ⊆ A [2-6].

Definition 2.2: A ternary Γ-ideal I of a ternary Γ-semigroup T is said to be pseudo symmetric provided x, y, z ∈T, 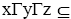I implies 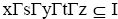for all s, t ∈T and I is said to be semi pseudo symmetric provided for any odd natural number n,x∈T,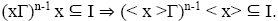

Theorem 2.3: Let I be a semi-pseudo symmetric ternary Γ-ideal of a ternary Γ-semigroup T. Then the following are equivalent.

1) I₁=The intersection of all completely prime ternary Γ-ideals of T containing I.

2) I₁¹ =The intersection of all minimal completely prime ternary Γ-ideals of T containing I.

3) 1₁^1I =The minimal completely semiprime ternary Γ-ideal of T relative to containing I.

4) I₂={x ∈ T: (xΓ)^n-1 x ⊆I for some odd natural number n}

5) I₃=The intersection of all prime ternary Γ-ideals of T containing I.

6) I₃¹ =The intersection of all minimal prime ternary Γ-ideals of T containing I.

7) I¹¹₃ =The minimal semiprime ternary Γ-ideal of T relative to containing I.

8) I₄={x ∈ T: (<x>Γ)^n-1< x > ⊆ I for some odd natural number n}.

Theorem 2.4: If I is a ternary Γ-ideal of a semi simple ternary Γ-semigroup T, then the following are equivalent. 1) I is completely semiprime.

2) I is pseudo symmetric.

3) I is semi-pseudo symmetric.

Results and Discussion

M (i)-ternary gamma-semigroup

We now introduce the terms I-dominant element and I-dominant ternary Γ-ideal for a ternary Γ-ideal of a ternary Γ- semigroup [7].

Definition 3.1: Let I be a ternary Γ-ideal in a Ternary Γ-semigroup T. An element x∈T is said to be I-dominant provided there exists an odd natural number n such that 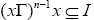A ternary Γ-ideal J of T is said to be I-dominant ternary Γ- ideal provided there exists an odd natural number n such that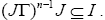

Note 3.2: If I is a ternary Γ-ideal of a ternary Γ-semigroup T, then every element of I is a I-dominant element of T and I itself an I-dominant ternary Γ-ideal of T.

Definition 3.3: Let I be a ternary Γ-ideal of a ternary Γ-semigroup T. An I-dominant element x is said to be a nontrivial Idominant element of T if x ∉ I.

Notation 3.4: M_o (I)=The set of all I-dominant elements in T.

M₁ (I)=The largest ternary Γ-ideal contained in M_o (I).

M₂ (I)=The union of all I-dominant ternary Γ-ideals.

Theorem 3.5: If I is a ternary Γ-ideal of a ternary Γ-semigroup T, the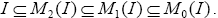

Proof: Since I is itself an I-dominant ternary Γ-ideal, and M₂ (I) is the union of all I-dominant ternary Γ-ideals. Therefore, I⊆M₂ (I). Let 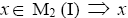belongs to at least one I-dominant ternary Γ-ideals 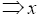is an I-dominant element. Hence, x∈M₀ (I). Therefore, 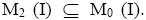Clearly M₂ (I) is a ternary Γ-ideal of T. Since M₁ (I) is the largest ternary Γ-ideal contained in M_o (I), we have 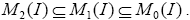Hence,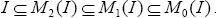

Theorem 3.6: If I is a ternary Γ-ideal in a ternary Γ-semigroup T, then the following are true.

1. M₀ (I)=I₂.

2. M₁ (I) is a semiprime ternary Γ-ideal of T containing I.

3. M₂ (I)=I₄.

Proof: (1) M_o (I)=The set of all I-dominant elements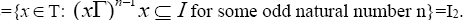

(2) Suppose that 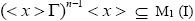for some odd natural number n. Suppose, if possible 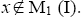M₁ (I), < x > are the ternary Γ-ideals implies 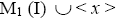is a ternary Γ-ideal. Since M₁ (I) is the largest ternary Γ-ideal in M₀ (I), We have 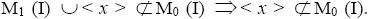Hence, there exists an element y such that 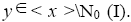Now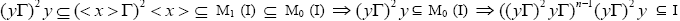 for some odd natural number 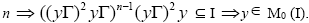It is a contradiction. Therefore, x ∈ M₁ (I). Hence, M₁ (I) is a semiprime ternary Γ-ideal of T containing I.

(3) Let x∈M₂ (I). Then there exists an I-dominant ternary Γ-ideal J such that x∈J.

J is I-dominant ternary Γ-ideal implies there exists an odd natural number n such that 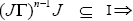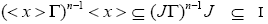for some odd 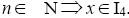Therefore,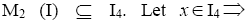 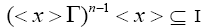for some odd n∈ N. So < x > is an I-dominant ternary Γ-ideal in T and hence,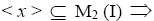 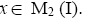Therefore, 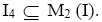Hence, 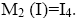It is natural to ask whether M₁ (I)=I₃. This is not true.

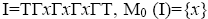
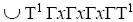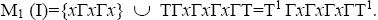Example 3.7: In the free ternary Γ-semigroup T over the alphabet x, y, z. For the ternary Γ-ideal and But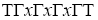 is a prime ternary Γ-ideal, let I, J, K are three ternary Γ-ideals of T such that 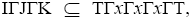implies all words containing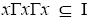or all words containing 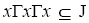or all words containing 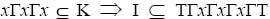or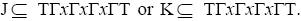 Therefore, 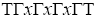is a prime ternary Γ-ideal. We have 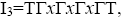so 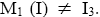Therefore, we can remark that the inclusions in 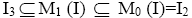may be proper in an arbitrary ternary Γ-semigroup [8-11].

Theorem 3.8: If I is a semi pseudo symmetric ternary Γ-ideal in a ternary Γ-semigroup T, then M₀ (I)=M₁ (I)=M₂ (I).

Proof: Suppose I is a semi pseudo symmetric ternary Γ-ideal in a ternary Γ-semigroup T. By theorem 3.7, M₀ (I)=I₂ and M₂ (I)=I₄. Also by theorem 2.10, we have I2=I₄. Hence, M₀ (I)=M₂ (I). By the theorem 3.5, 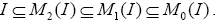We have 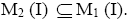Now let 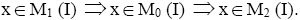Therefore, 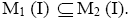Hence, 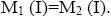Therefore,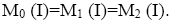

Theorem 3.9: For any semi pseudo symmetric ternary Γ-ideal I in a ternary Γ-semigroup T, a nontrivial I-dominant element 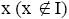cannot be semi simple [12,13].

Proof: Since x is a nontrivial I-dominant element, there exists an odd natural number n such that 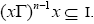Since I is semi pseudo symmetric ternary Γ-ideal, we have 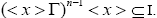If x is semi simple, then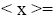 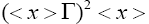and hence, 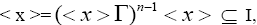this is a contradiction. Thus, x is not semi simple.

Theorem 3.10: If I is a ternary Γ-ideal in a ternary Γ-semigroup T, such that M₀ (I)=I, then I is a completely semiprime ternary Γ-ideal and I is a pseudo symmetric ternary Γ-ideal.

Proof: Let 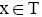and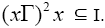 Since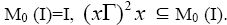 Thus, there exists an odd natural number n such that 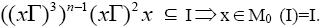Therefore, I is a completely semiprime ternary Γ-ideal. By corollary 2.11, A is pseudo symmetric ternary Γ-ideal. Hence, I is completely semiprime and pseudo symmetric ternary Γ-ideal.

Theorem 3.11: If I is a semi pseudo symmetric ternary Γ-ideal of a ternary semi simple Γ-semigroup then I=M₀ (I).

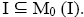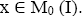Proof: Clearly, Let If 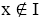then x is a nontrivial I-dominant element. By theorem 3.9, x cannot be semi simple. It is a contradiction. Therefore, 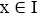and hence, 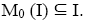Thus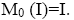

We now introduce a left I-divisor element, lateral I-divisor element, right, I-divisor element and I-divisor element corresponding to a ternary Γ-ideal A in a ternary Γ-semigroup.

Definition 3.12: Let I be a ternary Γ-ideal in a ternary Γ-semigroup T. An element 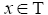is said to be a left I-divisor (a lateral I-divisor, right I-divisor) provided there exist two elements 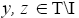such that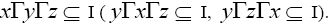

Definition 3.13: Let I be a ternary Γ-ideal in a ternary Γ-semigroup T. An element x∈T is said to be two-sided A-divisor if x is both a left I-divisor and a right, I-divisor element.

Definition 3.14: Let I be a ternary Γ-ideal in a ternary Γ-semigroup T. An element x∈T is said to be I-divisor if a is a left Idivisor, a lateral I-divisor and a right, I-divisor element.

We now introduce a left I-divisor ternary Γ-ideal, lateral I-divisor ternary Γ-ideal, right I-divisor ternary Γ-ideal and I-divisor ternary Γ-ideal corresponding to a ternary Γ-ideal I in a ternary Γ-semigroup.

Definition 3.15: Let I be a ternary Γ-ideal in a ternary Γ-semigroup T. A ternary Γ-ideal J in T is said to be a left I-divisor ternary Γ-ideal (lateral I-divisor ternary Γ-ideal, right I-divisor ternary Γ-ideal, two sided I-divisor ternary Γ-ideal) provided every element of J is a left I-divisor element (a lateral I-divisor element, a right I-divisor element, it is both a left I-divisor ternary Γ-ideal and a right I-divisor ternary Γ-ideal).

Definition 3.16: Let I be a ternary Γ-ideal in a ternary Γ-semigroup T. A ternary Γ-ideal J in T is said to be I-divisor ternary Γ-ideal provided if it is a left I-divisor ternary Γ-ideal, a lateral I-divisor ternary Γ-ideal and a right I-divisor ternary Γ-ideal of a ternary Γ-semigroup T.

Notation 3.17: R_l (I)=The union of all left I-divisor ternary Γ-ideals in T.

R_r (I)=The union of all right I-divisor ternary Γ-ideals in T.

R_m (I)=The union of all lateral I-divisor ternary Γ-ideals in T.

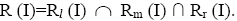We call R (I), the divisor radical of T.

Theorem 3.18: If I is any ternary Γ-ideal of a ternary Γ-semigroup T, then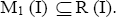

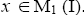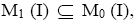Proof: Let Since we have 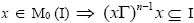for some odd natural number n. Let n be the least odd natural number such that 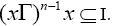If n=1 then x∈I and hence,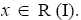

If n >1, then 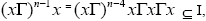where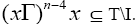

Hence, x is an I-divisor element. Thus, 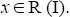Therefore,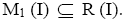

Theorem 3.19: If I is a ternary Γ-ideal in a ternary Γ-semigroup T, then R (I) is the union of all I-divisor ternary Γ-ideals in T.

Proof: Suppose I is a ternary Γ-ideal in a ternary Γ-semigroup T.

Let J be I-divisor ternary Γ-ideal in T. Then J is a left I-divisor, a lateral I-divisor and a right I-divisor ternary Γ-ideal in T. Thus 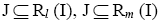and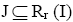

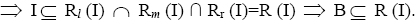
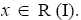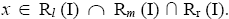Therefore, R (I) contains the union of all I-divisor ternary Γ-ideals in T. Let Then So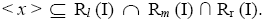

Hence, 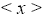is I-divisor ternary Γ-ideal. So, R (I) is contained in the union of all divisor ternary Γ-ideals in T. Thus R (I) is the union of all divisor ternary Γ-ideals of T.

Corollary 3.20: If I is a pseudo symmetric ternary Γ-ideal in a ternary Γ-semigroup T, then R (I) is the set of all I-divisor elements in T.

Proof: Suppose I is a pseudo symmetric ternary Γ-ideal in T. Let x be I-divisor element in T. Then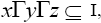 where y, z 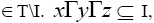I is pseudo symmetric

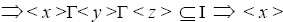is I-divisor ternary Γ-ideal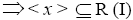

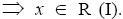Hence, R (I) is the set of all I-divisor elements in T. We now introduce the notion of M (I)-ternary Γ- semigroup.

Definition 3.21: Let I be a ternary Γ-ideal in a ternary Γ-semigroup T. T is said to be a M (I)-ternary Γ-semigroup provided every I-divisor is I-dominant.

Notation 3.22: Let T be a ternary Γ-semigroup with zero. If I={0}, then we write R for R (I) and M for M₀ (I) and M-ternary Γ-semigroup for M (I)-ternary Γ-semigroup.

Theorem 3.23: If T is an M (I)-ternary Γ-semigroup, then R (I)=M₁ (I).

Proof: Suppose T is an M (I)-ternary Γ-semigroup. By theorem 3.18,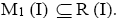

Let 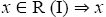is an I-divisor 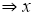is an I-dominant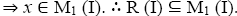

Hence,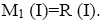

Theorem 3.24: Let I be a semipseudo symmetric ternary Γ-ideal in a ternary Γ-semigroup T. Then T is an M (I)-ternary Γ- semigroup iff R (I)=M₀ (I).

Proof: Since I is a semi-pseudo symmetric ternary Γ-ideal, by theorem 3.8, M₀ (I)=M₁ (I)=M₂ (I). If Tan M (I)-ternary Γ- semigroup, then by theorem 3.23, R (I)=M₁ (I). Hence, R (I)=N₀ (I). Conversely suppose that R (I)=M₀ (I). Then clearly every I-divisor element is an I-dominant element. Hence, T is an M (I)-ternary Γ-semigroup.

Corollary 3.25: Let I be a pseudo symmetric ternary Γ-ideal in a ternary Γ-semigroup T. Then T is an M (I)-ternary Γ- semigroup if and only if R (I)=M₀ (I).

Proof: Since every pseudo symmetric ternary Γ-ideal is a semi-pseudo symmetric ternary Γ-ideal, by theorem 3.24, R (I)=M₀ (I).

Corollary 3.26: Let T be a ternary Γ-semigroup with 0 and < 0 > is a pseudo symmetric ternary Γ-ideal. Then R=M iff T is an M-ternary Γ-semigroup.

Proof: The proof follows from the theorem 3.24.

Theorem 3.27: If N is a maximal ternary Γ-ideal in a ternary Γ-semigroup T containing a pseudo symmetric ternary Γ-ideal I, then N contains all I-dominant elements in T or T\N is singleton which is I-dominant.

Proof: Suppose N does not contain all I-dominant elements.

Let 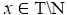be any I-dominant element and y be any element in T\N.

Since N is a maximal ternary Γ-ideal,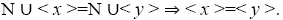

Since 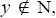we have 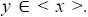Let n be the least positive odd integer such that 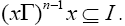Since I is a pseudo symmetric ternary Γ-ideal then I is a semipseudo symmetric ternary Γ-ideal and hence,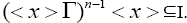

Therefore 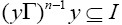and hence, y is I-dominant element. Thus, every element in T\N is I-dominant.

Similarly, we can show that if m is the least positive odd integer such that Therefore, there exists an odd natural number p such that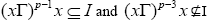 for all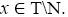

Let x, y, z ∈ T\N. Since N is maximal ternary Γ-ideal, we have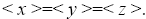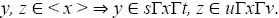

So So 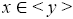and hence, x ∈ sΓyΓt for some s, t ∈ T₁. Now since I is a pseudo symmetric ternary Γ-ideal,

we have, 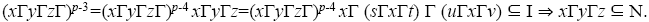If y ≠ x then s, t ∈ T. If s, t ∈ N then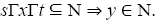

Which is not true. In both the cases we have a contradiction. Hence, x=y.

Similarly, we show that z=x.

Corollary 3.28: If N is a nontrivial maximal ternary Γ-ideal in a ternary Γ-semigroup T containing a pseudo symmetric ternary Γ-ideal I. Then M₀ (I) ⊆N.

Proof: Suppose in 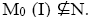Then by above theorem 3.27, N is trivial ternary Γ-ideal. It is a contradiction. Therefore, M₀ (I) ⊆N.

Corollary 3.29: If N is a maximal ternary Γ-ideal in a semi simple ternary Γ-semigroup T containing a semipseudo symmetric ternary Γ-ideal I. Then M₀ (I) ⊆N.

Proof: By theorem 3.11, I is pseudo symmetric ternary Γ-ideal. If 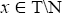is I-dominant, then x cannot be semi simple. It is a contradiction. Therefore, M₀ (I) ⊆ N.

Conclusion

According to theorem 3.11, I is pseudo symmetric ternary Γ-ideal. If x ∈ T\N is I-dominant, then x cannot be semi simple. Hence, is a contradiction. Therefore, M₀ (I) ⊆ N.

References

1. Anjaneyulu A.Stucture and ideals theory of semigroups. Thesis, ANU.1980.
2. MadhusudhanaRao D, Anjaneyulu A,GangadharaRao A. Pseudo symmetric Γ-Ideals in Γ-semigroups. Int J Math Eng.2011;116:1074-81.
3. MadhusudhanaRao D, Anjaneyulu A,GangadharaRao A. Prime Γ-radicals in Γ-semigroups. Int J Math Eng.2011;116:1074-81.
4. MadhusudhanaRao D, Anjaneyulu A,GangadharaRao A. N(A)-Γ-semigroups.Ind J Math Mathemat Sci.2011;7(2):75-83.
5. MadhusudhanaRao D. Primary ideals in quasi-commutative ternary semigroups. Int J Pure Alg. 2011;3(7):254-8.
6. MadhusudhanaRao D, SrinivasaRao G. A Study on ternary semirings. IntJ Mathemat Arch. 2014;5(12):24-30.
7. MadhusudhanaRao D, SrinivasaRao G. Special elements of a ternary semiring. Int J Eng Res and App.2014;4(11):123-30.
8. MadhusudhanaRao D, SrinivasaRao G. Concepts on ternary semirings. International Journal of Modern Science and Engineering Technology (IJMSET).2014;1(7):105-10.
9. MadhusudhanaRao D, Vasantha M,VenkateswaraRao M. Structure and study of elements in ternary Γ-semigroups. Int J Eng Res.2014;4(4):197-202.
10. MadhusudhanaRao D. N (A)-ternary semigroups. African J Math and Comp Sci Res. 2013;6(7):149-55.
11. Subramanyeswarao VB, Anjaneyulu A, MadhusudhanaRao D. Partially ordered Γ-semigroups.Int JEng Res Technol.2012;1(6):1-11.
12. Sarala Y,Anjaneyulu A,MadhusudhanaRao D. Ternary semigroups. Int JMathematSciTechnol and Human.2013;76:848-59.
13. Vasantha M, MadhusudhanaRao D. Properties of prime ternary-radicals in ternary-semigroups. Global Journal of Pure and Applied Mathematics.2015;1(6):4255-71.