Original Article
, Volume: 15( 4)Regular Ternary Semigroups
- *Correspondence:
- Jaya Lalitha G Department of Mathematics, KL University, Guntur, Andhra Pradesh, India, Tel: 040 2354 2127; E-mail: jayalalitha.yerrapothu@gmail.com
Received Date: May 27, 2017 Accepted Date: August 29, 2017 Published Date: September 04, 2017
Citation: Jaya Lalitha G, Sarala Y, Madhusudhana R. Regular Ternary Semigroups. Int J Chem Sci. 2017;15(4):191
Abstract
Intriguing properties of regular ternary semigroups and completely regular ternary semigroups were discussed in the article.
Keywords
Regular ternary semigroup; Completely regular ternary semigroup
Introduction
Los [1] concentrated a few properties of ternary semigroups and demonstrated that each ternary semigroup can be installed in a semigroup. Sioson [2] concentrated ideal theory in ternary semigroups. He likewise presented the thought of regular ternary semigroups and characterized them by utilizing the thought of quasi ideals. Santiago [3] built up the theory of ternary semigroups and semiheaps. Dutta and Kar [4,5] presented and concentrated the thought of regular ternary semirings. Jayalalitha et al. [6] presented and learned about the filters in ternary semigroups. As of late, various mathematicians have taken a shot at ternary structures. In this paper, we concentrate some intriguing properties of regular ternary semigroups and completely regular ternary semigroups.
Definition 1
An element x in a ternary semigroup T is said to be a regular if Ǝ an element 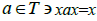 [2].
[2].
A ternary semigroup is said to be regular if all of its elements are regular.
Theorem 1
The following conditions in a ternary semigroup T are equivalent:
(i) T is regular.
(ii) For any right ideal R, lateral ideal M and left ideal L of T, 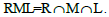
(iii) For 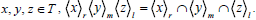
(iv) For 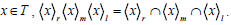
Proof
(i) ⇒ (ii) Suppose T is a regular ternary semigroup. Let R, M and L be a right ideal, a lateral ideal and a left ideal of T.
Then clearly, 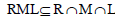 . Now for
. Now for 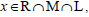 we have x=xax for some a
we have x=xax for some a T . This implies that
T . This implies that

Thus, we have 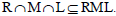 So we find that
So we find that 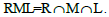
Clearly, (ii) ⇒ (iii) and (iii) ⇒ (iv) .
It remains to show that (iv) ⇒ (i) .
Let x 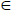 T .Clearly,
T .Clearly,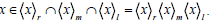
Then we have, 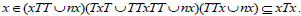
So we find that x 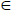 xTa and hence there exists an elements a
xTa and hence there exists an elements a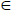 T such that x=xax. This implies that x is regular and hence T is regular.
T such that x=xax. This implies that x is regular and hence T is regular.
We note that every left and right ideal of a regular ternary semigroup may not be a regular ternary semigroup.
However, for a lateral ideal of a regular ternary semigroup, we have the following result:
Lemma
Every lateral ideal of a regular ternary semigroup T is a regular ternary semigroup.
Proof
Let L be a lateral ideal of regular ternary semigroup T. Then for each x 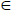 L there exists a
L there exists a 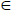 T such that x=xax. Now
T such that x=xax. Now
x=xax=xaxax=x(axa)x=xpx where p= axa 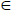 L. This implies that L is a regular ternary semigroup.
L. This implies that L is a regular ternary semigroup.
Definition 2
An ideal A of a ternary semigroup T is said to be a regular ideal if 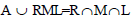 for any right ideal
for any right ideal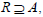
lateral ideal 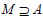 and left ideal
and left ideal 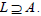
Remark 1
From Definition 2, it follows that T is always a regular ideal and any ideal that contains a regular ideal is also a regular ideal.
Now if for any right ideal R, lateral ideal M and left ideal L; RML contains a regular ideal, then 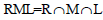
Proposition
A ternary semigroup T is a regular ternary semigroup if and only if {0} is a regular ideal of T.
Proof
Let P be the nuclear ideal of a ternary semigroup T. i.e., the intersection of all non-zero ideals of T, Pr is the intersection of all non-zero right ideals of T, Pm is the intersection of all non-zero lateral ideals of T and Pl is the intersection of all non-zero left ideals of T. Now if P={0}, then clearly P=Pr=Pm=Pl.
Theorem 2
Let T be a ternary semigroup and P=Pr=Pm=Pl. Then T is a regular ternary semigroup if and only if P is a regular ideal of T.
Proof
If P=Pr=Pm=Pl={0}, then proof follows from proposition. So we suppose that,
P=Pr=Pm=Pl ≠ {0}. Let T be a regular ternary semigroup. Then from proposition, it follows that {0} is a regular ideal of T.
Now, 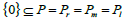 implies that P is a regular ideal of T, by using Remark 1.
implies that P is a regular ideal of T, by using Remark 1.
Conversely, let P be a regular ideal of T. Then 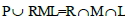 for any right ideal
for any right ideal 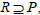 lateral ideal
lateral ideal 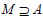 and left ideal
and left ideal 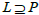 of T. Since PPP is a right ideal of T and P=Pr, we have
of T. Since PPP is a right ideal of T and P=Pr, we have 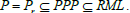
Consequently, 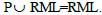 So
So 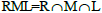 and hence from Theorem 2, it follows that T is a regular ternary semigroup.
and hence from Theorem 2, it follows that T is a regular ternary semigroup.
Corollary 1
Let T be a ternary semigroup and P=Pr=Pm=Pl. Then T is a regular ternary semigroup if and only if every ideal of T is regular.
Proof
Suppose T is a regular ternary semigroup. Then from Theorem 2, it follows that P is a regular ideal of T. Now P=Pr=Pm=Pl implies that every non-zero ideal of T contains the regular ideal P of T. Consequently, by using Remark 1, we find that every ideal of T is regular.
Conversely, if every ideal of T is regular, then P is a regular ideal of T and hence from Theorem 2, it follows that T is a regular ternary semigroup.
Theorem 3
The following conditions in a ternary semigroup T are equivalent:
(i) A is a regular ideal of T.
(ii) For 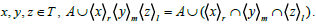
(iii) For 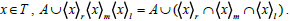
(iv) For each 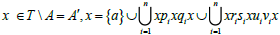 for some
for some 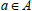 and
and 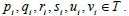
Proof
(i) ⇒(ii) Suppose A is a regular ideal of T. We note that for x, y, z 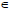 T ,
T ,
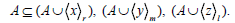
Now 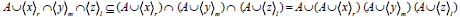 (since A is regular).
(since A is regular).
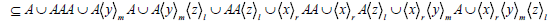
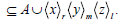
Again 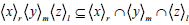 implies that
implies that 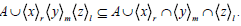
So we find that 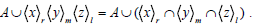
ii) ⇒ (iii) Put y=z=x in (ii) we get (iii).
(iii) ⇒ (iv)We first note that 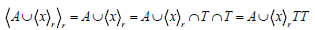
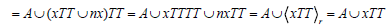
Similarly we have, 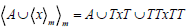 and
and 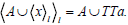
Now 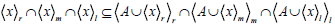
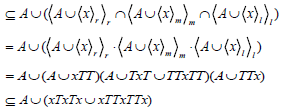
Since, 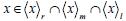 there exists
there exists  and
and  such that
such that
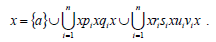
(iv) ⇒ (i) Let R, M and L be any right, lateral and left ideal of T respectively such that 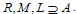 Then clearly,
Then clearly,
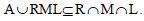 Again, let
Again, let 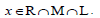 Then by using condition (iv), we have
Then by using condition (iv), we have 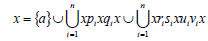 for some
for some 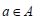 and
and 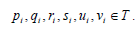 Since
Since 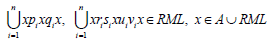 and hence
and hence 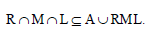 Thus
Thus 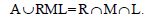 Consequently, A is a regular ideal.
Consequently, A is a regular ideal.
Theorem 4
Let A be a regular ideal of a ternary semigroup T. For any right ideal R, lateral ideal M and left ideal L of T, if 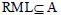 then
then 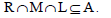
Proof
Suppose for any right ideal R, lateral ideal M and left ideal L of T, 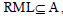 where A is a regular ideal of T. Then
where A is a regular ideal of T. Then
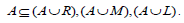
Now 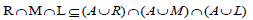
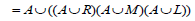 [Since A is regular]
[Since A is regular]
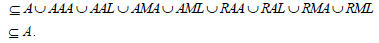
From Theorem 4, we have the following results:
Corollary 2
A regular and strongly irreducible ideal of a ternary semigroup T is a prime ideal of T.
Corollary 3
Every regular ideal of a ternary semigroup T is a semi prime ideal of T.
Theorem 5
Proof
Let T be a regular ternary semigroup and A be any ideal of T. Then 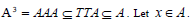 Then there exists
Then there exists 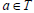 such that x=xax=xaxax. Since A is an ideal and
such that x=xax=xaxax. Since A is an ideal and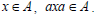 Thus
Thus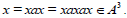
Consequently, 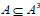 and hence
and hence 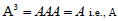 is idempotent.
is idempotent.
Conversely, suppose that every ideal of T is idempotent. Let P, Q and R be three ideals of T. Then 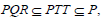
 This implies that
This implies that 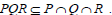 Also,
Also,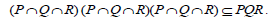 Again, since
Again, since 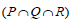 is an ideal of T,
is an ideal of T,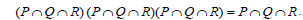 Thus
Thus 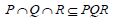 and hence
and hence 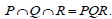 Therefore, by Theorem 2, T is a regular ternary semigroup.
Therefore, by Theorem 2, T is a regular ternary semigroup.
Theorem 6
A ternary semigroup T is left (resp. right) regular if and only if every left (resp. right) ideal of T is completely semiprime.
Proof
Let T be a left regular ternary semigroup and L be any left ideal of T. Suppose 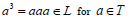 Since T is left regular, there exists an element
Since T is left regular, there exists an element 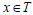 such that
such that 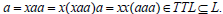 Thus L is completely semiprime.
Thus L is completely semiprime.
Conversely, suppose that every left ideal of T is completely semiprime. Now for any 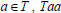 is a left ideal of T. Then by hypothesis, Taa is a completely semiprime ideal of T. Now
is a left ideal of T. Then by hypothesis, Taa is a completely semiprime ideal of T. Now 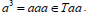 Since Taa is completely semiprime, it follows that
Since Taa is completely semiprime, it follows that 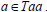 So there exists an element
So there exists an element 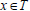 such that a=xaa. Consequently, a is left regular. Since a is arbitrary, it follows that T is left regular.
such that a=xaa. Consequently, a is left regular. Since a is arbitrary, it follows that T is left regular.
Equivalently, we can prove the Theorem for right regularity.
Completely Regular Ternary Semigroup
Definition 3
A pair (p, q) of elements in a ternary semigroup T is known as an idempotent pair if pq(pqx)=pqx and (xpq)pq=xpq for all 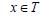 [3].
[3].
Definition 4
Two idempotent pairs (p, q) and (r, s) of a ternary semigroup T are known as an equivalent, if pqx=rsx and xpq=xrs for all 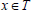 [3].
[3].
In notation we write (p, q) ~ (r, s).
Definition 5
An element x of a ternary semigroup T is said to be completely regular if Ǝ an element 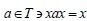 idempotent pairs (a, x) and (x, a) are equivalent.
idempotent pairs (a, x) and (x, a) are equivalent.
If all the elements of T are completely regular, then T is called completely regular [3].
Definition 6
An element x of a ternary semigroup T is known as a left regular if Ǝ an element 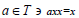
Definition 7
7 An element x of a ternary semigroup T is said to be right regular if Ǝ an element 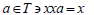
Theorem 7
A ternary semigroup T is completely regular then T is left and right regular. 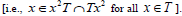
Proof
Suppose T is a completely regular ternary semigroup. Let 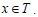 Then Ǝ an element
Then Ǝ an element 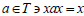 and the idempotent pairs (x, a) and (a, x) are equivalent i.e., xab=axb and bxa=bax for all
and the idempotent pairs (x, a) and (a, x) are equivalent i.e., xab=axb and bxa=bax for all 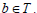 Now in particular, putting b=x we find that xax=axx and xaa=xax. This implies that
Now in particular, putting b=x we find that xax=axx and xaa=xax. This implies that 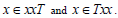 Hence T is left and right regular.
Hence T is left and right regular.
Theorem 8
A ternary semigroup T is left and right regular then 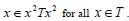
Proof
Suppose that T is both left and right regular. Let 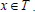 Then
Then 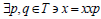 and and x=qxx. This implies that
and and x=qxx. This implies that
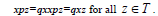
Now x=xxp=x(xxp)p=x2(xpp)=x2(qxxpp)=x2(qxp)=x2q(qxx)p=x2 q2(xxp)=x2 q2x=x2 q2qxx=x2 q3x2 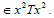 Hence
Hence 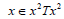 for all
for all 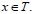
Theorem 9
If T is ternary semigroup 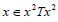 for all
for all 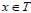 then T is completely regular.
then T is completely regular.
Proof
Suppose 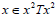 for all
for all 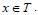 Then
Then 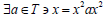
Now 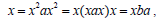 where
where 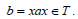 This implies that T is regular. Also
This implies that T is regular. Also 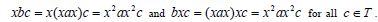 This shows that the idempotent pairs (x, b) and (b, x) are equivalent.
This shows that the idempotent pairs (x, b) and (b, x) are equivalent.
Consequently, T is a completely regular ternary semigroup.
Definition 8
A sub semigroup S of a ternary semigroup T is said to be a bi-ideal of T if 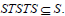
Theorem 10
A ternary semigroup T is completely regular ternary semigroup if and only if every bi-ideal of T is completely semiprime.
Proof
Let T is a completely regular ternary semigroup. Let P be any bi-ideal of T. Let 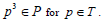 Since T is completely regular, from Theorem 10, it follows that
Since T is completely regular, from Theorem 10, it follows that 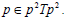 This implies that there exists
This implies that there exists 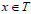 such that
such that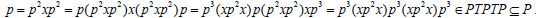 This shows that P is completely semiprime.
This shows that P is completely semiprime.
Conversely, assume that every bi-ideal of T is completely semiprime. Since every left and right ideal of a ternary semigroup T is a bi-ideal of T, it follows that every left and right ideal of T is completely semiprime. Consequently, we have from Theorem 6 that T is both left and right regular. Now by using Theorem 9, we find that T is a completely regular ternary semigroup.
Theorem 11
If T is a completely regular ternary semigroup, then every bi-ideal of T is idempotent.
Proof
Let T be a completely regular ternary semigroup and P be a bi-ideal of T. Clearly T is a completely regular ternary semigroup. Let 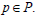 Then there exists
Then there exists 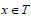 such that p=pxp. This implies that
such that p=pxp. This implies that 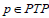 and hence
and hence 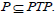 Also
Also 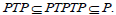 Thus we find that P=PTP. Again, we have from Theorem 11 that
Thus we find that P=PTP. Again, we have from Theorem 11 that 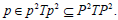 This implies that
This implies that 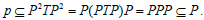 Hence
Hence 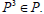 Therefore every bi-ideal of P is idempotent.
Therefore every bi-ideal of P is idempotent.
Conclusion
Ternary structures and their speculation, the purported n-ary structures bring certain expectations up in perspective of their conceivable applications in organic chemistry.
References
- Los J. On the extending of models I. Fund Math. 1955;42:38-54.
- Sioson FM. Ideal theory in ternary semigroups. Math Japonica. 1965;10:63-84.
- Santiago ML. Some contributions to the study of ternary semigroups and semiheaps. Ph.D. Thesis. University of Madras 1983.
- Dutta TK, Kar S. On regular ternary semirings. Advances in Algebra, Proceedings of the ICM Satellite Conference in Algebra and Related Topics, World Scientific 2003;343-55.
- Dutta TK, Kar S. A note on regular ternary semirings. Kyungpook Mathematical Journal 46:357-65.
- Jayalalitha G, Sarala Y, Srinivasa Kumar B, et al. Filters in ternary semigroups. Int J Chem Sci. 2016;14:3190-4.
