Short communication

, Volume: 12( 2) DOI: 10.37532/2320–6756.2023.12(2).260

• View PDF
• Download PDF

ON OPTIMAL TRAJECTORY IN SPACE FLIGHT

*Correspondence:

Sergey Orlov Professional researcher of Petrozavodsk State University, Russia, E-mail:ion@sampo.ru

Abstract

 This article investigated a trajectory of new type in distant, space flights unlike usual trajectories of direct flight to heavenly object (Moon) it is supposed to use asymmetry of a gravitational field and to carry out flight bypassing the most power gravitational impact on the spacecraft. It leads to economy of power for 20%-30%.

Keywords

The theory of vortex gravitation; Space flights with an optimum trajectory

Introduction

Now in a science there is a statement that force of gravitation is created by any body. According to this law force of gravitation decreases under the law of a return square of distance from this body equally in all directions. In the theory of vortex gravitation proposed study, the force of gravity - a force push, which is caused by the decrease in pressure in the space medium called ether. In turn pressure reduction in heavenly points is caused by vortex rotation of ether round these points, according to hydro aerodynamics laws [1]. Speed of orbital rotation of streams of each whirlwind is inversely proportional to distance from square of center of this whirlwind. As the whirlwind rotates in one plane, and the law of dependence of speed, pressure and force of gravitation from square of distance to the center of rotation of ether, operates too only in one plane of rotation of ether. In calculations are made to prove that point in the sky, which has a deviation from the plane of rotation of the ether, the gravitational force (push) acting on this point, is reduced in proportion to the cube of the distance to that point from the gravitational plane [1]. In general, the force of gravity can be calculated by the formula 26 [1]

Fgv = Fgn Cos3ϕ ,                               (1)

Where, Fgn - the force of gravity in the two-dimensional model (Eq. 10 in [1], which corresponds to the empirical formula for the law of universal gravitation Newton)

Fgv - The force of gravity in a three-dimensional vortex model. φ - The angle between the straight line connecting the center of the torsion from this point, and the plane gravitational torsion.

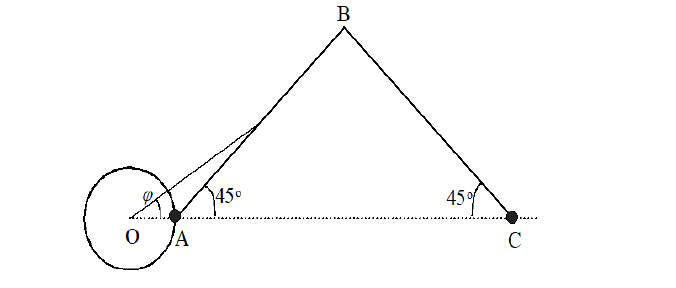
The location of the plane of cosmic torsion can determine the coordinates of celestial bodies-satellites of the torsion. In the solar system, the heliocentric latitude, the gravitational torsion coincide with latitude of the center of the perihelion and aphelion of the orbits of all the planets. The earth latitude, the gravitational torsion coincide with latitudes of apogee and perigee of the orbit of the moon. Thus, the coordinates of the gravitational torsion, we can determine the coordinates of the plane in which the gravitational force decreases at the lower, that is inversely proportional to the square of the distance from the center of torsion. As Earth is in the center earht gravitational torsion, at removal from it at distant space flights it is necessary to move to detour earth torsion, instead of on a direct trajectory, as in case of flight on the Moon. The following shows the calculation of the physical work required to make the spacecraft during flight to the moon in two different routes. Let’s consider a problem of comparing the works expended on getting over the gravitation attraction Forces (F) by a body, when traveling from point A to point C by the paths AC and ABC at two different F(r, ϕ ) dependences (FIG.1). The OAS line–a face projection gravitational torsion of Earth.

Gravitational interaction is characteristic of all bodies in the Universe and manifests itself in their mutual attraction to each other. Gravitational interaction occurs through a gravitational field that exists around a star, planet, etc. Thanks to gravitational interaction, the Earth gives all bodies near its surface acceleration according to the law of universal gravity. The law of universal gravity has certain boundaries, which allows you to overcome gravity. The article describes ways to overcome gravity, as well as an approach to the development of the universe (FIG. 1).

In this Figure O-Centre of Earth, A-Start of flight, C-Moon (finish), AC and ABC-Projections of Gravitational Flats. Note. In Figure 1, AC and ABC lines do not show flight paths, but lateral projections of the planes in which these flights are performed.

In the first case, F is independent of ϕ and obeys the Newton law

where m1 and m2 are the masses of bodies, G is the gravitation constant, and r is the distance between the bodies. In the second case, F depends on ϕ in accordance with formula:

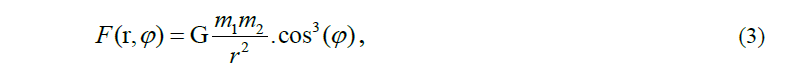
where ϕ is the angle between axis OC and the position radius-vector of the replaced body.

A is known, the work equals to the path integral:

Let A_AC be the work expended at the transference A_C for the case of the dependence (2). We determine the works AAB and ABС. For A’_AC being the work expended at the transference AC for the case of the dependence (2) we determine, respectively, the works A’_AB and A’BС.

Now we write the integral (4) for each case

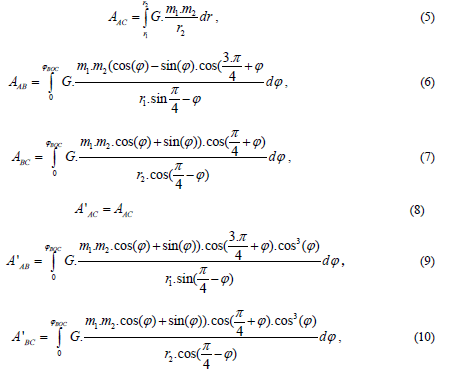
where r₁ is the distance OA,r₂–OC and ϕ BOC is the angle BOC

Formula (8) is valid because, in this direction, the forces (5) and (6) are equal to each other.

Calculating the integrals (7-10) numerically for the case of moonflight(r₁=6400∙103 m, r₂= 40000000m, m₂=6∙1024 kg, m₁=1 kg),one obtains A_AC= 6.1554643 ∙107A_AB =6.1140242 ∙107 J, A_BC= 4.1440045 ∙104 J, A’_AB= 4.5279719 ∙107 J, A’_BC=3.5727542 ∙105 J.

One can see that A_AC= A_AB+A_BC, which just must be the case for the Newtonian forces when the work does not depend on the transference path from point A to point С

In the case of the law (3), the work on the path ABC equals to A’_ABС= A’_AB+A’_BC= 4.5636994∙10⁷ J. This is less than the work A’_AС = A_AC = 6.1554643∙107 J.

The ratio (decrease) of the works is s=A’_ABС / A_AC = 0.7414062. The value of s depends on the distances r₁ and r₂ and on the transference path.

Thus, the transference by the path ABC in the case of the law (3) is more energetically preferable than that directly by the path AC

The above calculation shows that the moonflight with a detour of the Earth torsion should decrease the fuel consumption on 25%. At present, most interplanetary cosmic apparatus get accelerations which can not be explained on the basis of cosmic calculations in the relativity theory of Einstein. Particularly, deviations have been found for the apparatus of “Galileo”, “Rosetta” and “Cassini”. The suggested model of vortex gravitation (formula 3) shows that, if the trajectory of the satellite flight does not coincide with the Sun gravitation torsion plane, then one should take into account the value of gravitation coefficient in the calculation of solar gravity acting onto the satellites. This coefficient (Cos3ϕ ) reduces the value of solar gravity, which gives certain acceleration to cosmic satellites and results in a deviation of the motion trajectory [2,3].

References

1. Orlov S. Foundation of vortex gravitation, cosmology and cosmogony. Glob. j. sci. Front. res., Physic Space Sci. 2011;12(1).

   [Google Scholar]

2. Kiknadze LV, Yu GM. Classical hydrodynamics for physicistsexperimentalists. Tbilisi University Press. Tbilisi, Georgia. 1979:136.

   [Google Scholar]

3. Baatar T, Kulikov EG. Justification of VVER-1000 safety when using fuel compositions doped by protactinium and neptunium. Nuclear Energy and Technology. 2020;6(2):99-104.

   [Google Scholar]