Research

, Volume: 21( 1) DOI: 10.37532/0974-7486.21.001

• View PDF
• Download PDF

Modelling the Mechanisms of the Processes Quantum Conversion Energy and the Performances in Gas Dynamics Laser GDLS

*Correspondence:

Mohammedi Ferhat
Department of Physics, University of Mohamed Khider Biskra, Biskra, Algeria
E-mail: farwane@yahoo.fr

Abstract

In this paper we present the design and discus the performances and develop the mechanisms of the physics process of continuous gas laser dynamics GDLs, based on molecules N₂ (v=1)→CO₂ (001) (v=3). The main objectives of work in this area are, obtaining the high laser energies in short time durations needed for the feasibility studies the physical principles that can be used to make laser sources capable of delivering high average powers. We note that, in order to reach both objectives, one has to convert electrical or chemical energy into laser energy, using dense gaseous media. The process generating the wave excited, on the basis of the excited level vibration, theoretical predictions are compared with computer simulation.

Keywords

Modelling process; Lasers; Populations inversion; Pumping; Simulation

Introduction

A sufficiently high population of the vibrational and rotational states of a molecule may be achieved by thermal excitation. To this end, a gas mixture should be heated to temperatures in the range of 1000°K-2000°K. This simple rise of temperature cannot, of course, produce a population inversion, as in equilibrium the level is populated less, the higher its energy. In the first part of this paper we set up the equations for the model. These are on the one hand the equilibrium evolution equations and on the other hand the equations excitation relaxation within gas media. We shall show the elements of coupling the two systems. In the second part we present analytical method for solving these two systems and describe how they are coupled. In the third part we apply this model to the simulation of the various phases of flow gas in nozzles and relaxation in optical cavity [1].

The purpose of the present paper is to give a simple and efficient program for the numerical solution of the rate equations based model and analysis of the optical gain in the active region of the gas dynamics laser GDLs. An easy to use MATLAB user interface is provided. In order to find an optimal design of the structure for operation at specific wavelength and temperature, optimization procedure is provided as well [2]. The procedures for calculation of the quantum transitions rates is also included both with and without number of molecules are pumped into the gain region. The molecule distribution over the states of the system is found by solving the full set of rate equations which describe the transitions between levels, and subsequently used to determine the optical gain. These results can be easily calculated by a moderate PC configuration using the MATLAB programs provided, due to efficient numerical implementation. This is important, since the number of levels involved is inversely proportional to the applied compressible gas.

Materials and Methods

Theoretical considerations

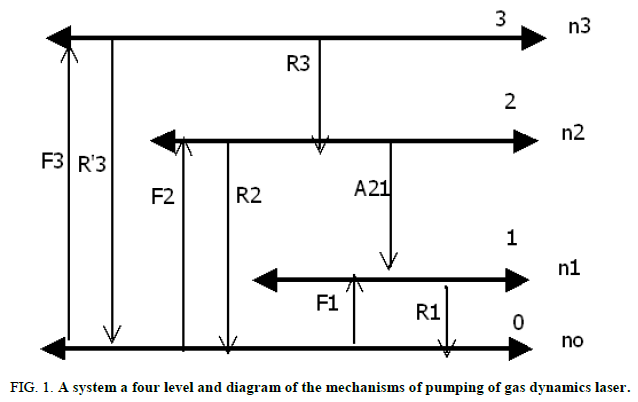
Condition of inversion of populations models on 4 levels stationary pumping: The following mechanism has been used to describe the theoretical results with simulation (Figure 1).

F: Term of excitation, R: Is relaxation term much previous work systems is based on rate equation analysis of a four level system, shown in this figure, the primary mission in this paper has been the development of a pumping energy transfer model in gas dynamic laser. Previous work using a four level system described by:

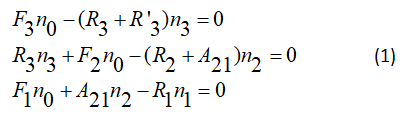
By introducing the notations defined by

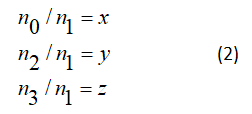
The equations of the assessment in the form of the system of equations according to

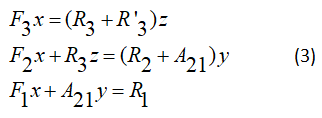
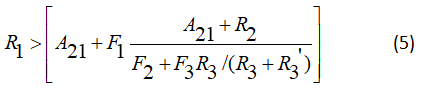
We can write

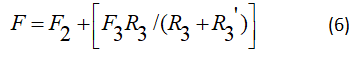
In the case

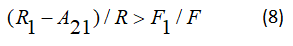
Gives the ration of

We can obtain the evolution for the system relaxation-excitation in equation (10) becomes

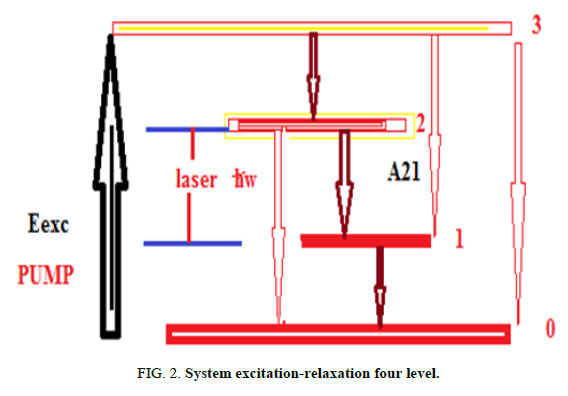
Quantum yield and energetic efficiency: The choice of a diagram of the energy levels of the active centre and of a method of pumping mainly conditions the value of the output of the laser, in Figure 2 the red purposes arrows designate the parasitic transitions and the brown full arrows designate desirable transition, suppose that the active centre is described by a diagram on four levels, η' is quantum yield of a laser (Figure 2).

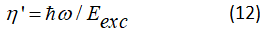
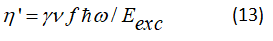
This parameter γ is power-factor absorbed by the active centers towards level 3, ν is power factor absorbed by the active centers towards level 2, f the ratio of the elements as A₂₁/F₂.

The factor term γ in equation (15) believes with the increase in the fraction of power absorbed by active centers, in our model active media with type (3→0, 3→1 and 2→0) transitions are not likely to be used to increase the factor ν and f.

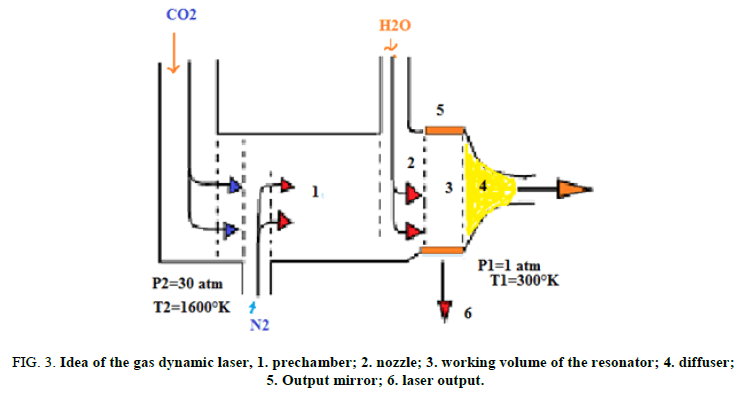
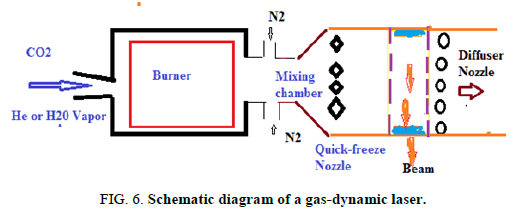
The gas dynamic CO₂ laser: This laser uses a mixture of carbon dioxide, nitrogen and water vapour as its active medium. The mixture typically contains 8% CO₂, 90% N₂ and 2% H₂0. The active centres are the CO₂ molecules. The idea of the gas dynamic laser design is illustrated in Figure 3. Upstream of the nozzle, the gas mixture is brought to the operational condition of the temperature T2=1600° K and pressure P2=20-30 atm. Behind the nozzle block a set of slits each 1 mm wide the gas expands so that its temperature falls to T1=250°K-300°K and pressure to P1=0.05-0.1 atm. The flow rate downstream of the nozzle is as high as 1200 m/s to 1500 m/s. The excited CO₂ molecules lase in the working chamber. Then the gas flow meets the diffuser provided for decelerating the flow and matching its pressure with the atmosphere.

The inversion production mechanism in the gas dynamic CO₂ laser

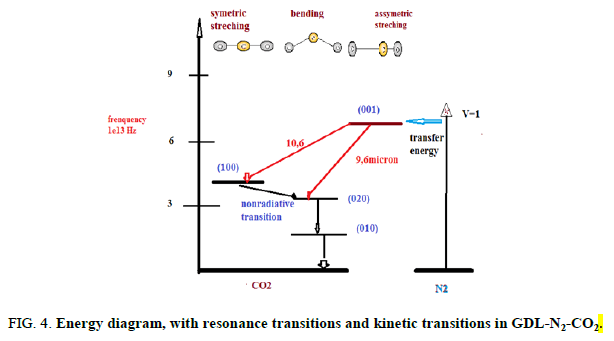
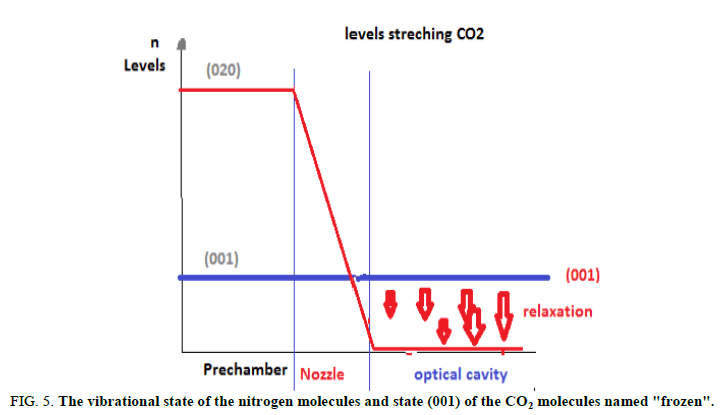
Similar to other types of CO₂ lasers, here the population inversion is obtained between the (001) and (100) states and (001) and (020)states of the CO₂ molecule. The processes of resonant energy transfer from the N₂ molecules take an important part inpopulating the (001) upper laser level. Water molecules introduced into the mixture aid in rapid sweeping out lasing molecules inthe (010) state. The thermodynamic pumping is remarkable in that now the vibrational states of the N₂ and CO₂ molecules arepopulated through thermal" rather than electronic, excitation. It is essential that the excited vibrational level of the N₂ moleculeand state (001) of the CO₂ molecule depopulate slower than states (100), (020) and (010). Assume that the CO₂ + N₂ gas mixtureheated to 1500 K rapidly expands in passing through a nozzle. Downstream from the nozzle, where the gas velocity runs into thesupersonic 1500 m/s, the kinetic energy of the molecules increases considerably. This translation energy increases at the expeneeof the vibrational motion in the molecules [3]. Therefore, behind the nozzle the vibrational states are swept out in the ground staterapidly. It is important that not all the levels undergo rapid decay, but exactly those having shorter lifetimes, that is, the lowerlaser levels of the CO₂ molecule. As for the (001) state of the CO₂ molecule and the vibrational level of the N₂ molecule, there issimply not enough time for them to somewhat relaxate in the rapid gas expansion. When in the laser volume, with a sufficientlyrarefied gas medium, these levels fail to deactivate by collisions practically altogether and the vibrational state of the nitrogenmolecules and state (001) of the CO₂ molecules are said to be “frozen”. The behaviour of the population for states (001) and(020)of the CO₂ molecule passing from the prechamber (at T2 and P2) to the working volume (at T1 and PI) is presented infigures. In the transition region around the nozzle, the (020) level is almost completely removed to the ground state, while state (001)suffers only insignificant loss of its population. As a result, a population inversion occurs between these states. Thus, CO₂molecules arrive at the working volume having practically unpopulated lower lasing levels (more precisely, “having thepopulation of these levels at T1). The upper laser level turns out to be populated as if the gas remained at temperature T2. It is ofconsequence that the population of the vibrational level of the N₂ molecules is also frozen. These excited molecules will givetheir energy to the CO₂ molecules through resonant collisions and maintain the relatively high population of the (001) level.Recall that the nitrogen is the prevalent component in the gas mixture (about 90%). Therefore, its vibrational energy is believedto be a chief source of energy for the coherent radiation. To sum up, the gas dynamic laser spends the energy stored in thevibrational degrees of freedom of the molecules arriving at the nozzle as follows [4]. The fraction of the energy stored in thesymmetric stretching and bending oscillations of the CO₂ molecules converts into the translation energy of the flow leaving thenozzle. The energy stored in the asymmetric stretching oscillations of the CO₂ molecules and what is more important, inoscillations of the nitrogen a molecule converts (minus losses in the resonator) into the energy of the coherent radiation of thelaser (Figures 4 and 5).

Improved performances of gas dynamics laser

A relatively low yield not exceeding 4% of gas dynamics lasers is due to several causes. Above all the energy of the translational movement of the translational gaseous stream coming out the nozzle is expended in pure loss, after braking and compression in the diffuser the gas is brought to high temperature. In addition the stream of the gas leaving the cavity carries a certain amount of excited N₂ molecules which have not had time to transfer the excitation energy to the CO₂ molecules as well as certain amount of excited CO₂ molecules which have not arrived at get off. To raise the efficiency of laser dynamics gas it is necessary to reduce the losses indicated [5]. The reduction of the losses related to the departure of the excited molecules of the cavity can be obtained by optimization of the parameters of the cavity and by improvement of its construction. For the losses related to the heating of the gas in the diffuser, their reduction requires to take more radical measures. It is possible to produce a dynamic gas laser with circulation of the gas mixture in closed circuit. Such a laser must have to additional organs: A compressor and a heat exchanger. They are intended to restore the gas mixture to the initial temperature and pressure. Thus, the energy of the translational movement of the gas stream can be used also to return the gas to its initial state. In this case, the dynamic gas laser is similar to a thermal machine operating in a close cycle of model Carnot cycle. As soon as such a laser enters into oscillation, the contribution of energy from the outside will only have to compensate the losses due to the movement of the gas in the cavity and the radiated light energy (Figure 6).

Gas dynamic considerations

The performance of a GDL is highly influenced by the rate of expansion and freezing of the gases through a minimum length contoured supersonic nozzle, a variety of GDL nozzles, nozzle arrays and nozzle perforated plates were investigated to determine the optimum operational regimes. See Figure 6 in supersonic nozzle design the conventional two dimensional nozzle is usually considered to consist of several regions as shown in Figure 1, these are:

• The contraction, in which the flow is entirely subsonic.
• The throat region, in which the flow accelerates from a high subsonic to a low supersonic speed.
• An initial expansion region, where the slope of the contour increases up to its maximum value.

The equations of motion assume such a form that they may be solved graphically, in a step by step process. The gas is to be accelerated to uniform and parallel supersonic flow at the desired Mach number.

Numerical simulation

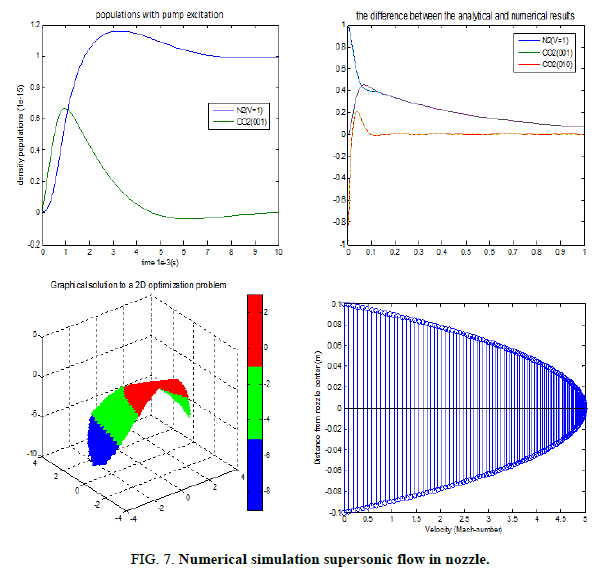
Each computational run is based on the integration of one initial condition with a well-known Runge-Kutta-ODE45 (Dormand-Prince) integrator scheme. As the integration progresses, this is repeated for several conditions and parameters, thus returning a complete description about the predictability of the used equations model [6].

These techniques are general enough to apply to different models with minor modifications. Our work focuses on the decay of the lasing levels is independent of the stimulated coupling of the laser level (Figure 7) [7].

Running the program and examples: In the following examples, applications of Gas Dynamic Laser (GDls) program are presented. We illustrate how the program can be used to obtain:

• A gain maximized structure
• Laser output properties in optical cavity diffuser.

The following is a pseudo code presentation of the algorithm of the main program:

Algorithm:

• Step 1: Choose the working fluid and provide its properties.
• Step 2: Enter the total mass flow rate and the number of nozzles.
• Step 3: Enter the required Mach number at the nozzle exit.
• Step 4: Initialize the calculation and evaluate the scale factor by comparing the area required by the mass flow rate andthe area of the unit model.
• Step 5: Choose the appropriate unit model among the available database according to the required Mach number at thenozzle exit.
• Step 6: Plot the x-y profile of nozzle from the final array.

Results and Discussion

An enhancement in mixationl reaction as well as mixing efficiency in the supersonic combustor is highly desirable in a development of efficient GDL laser. In this regard, the injection angle formed by two streams of species would play an important role in the gas dynamics laser GDLs cavity [8]. A higher injection angle was found to incur strong oblique shock wave and its subsequent reflections in the primary flow so that the field temperature increased highly enough to activate chemical reactions and produce more excited CO₂ molecules. However, so did the static pressure. Consequently, the molecular collision rate related to the whole laser system performance might increase. Regarding the effects of N₂ injection angles in the GDLs laser system on the population inversion and laser characteristics, the following has been found [9]. The calculation procedure is not subject to any doubt and to compare the results of the present simulation with the theory we calculated the gain coefficients as applied to the conditions of our numerical simulation for combustion products of a stoichiometric CO₂+N₂ mixture expanding in a supersonic nozzle; the equilibrium composition of the mixture was CO₂:N₂:H₂0=2:10:1.

Conclusion

The molecule distribution over the states of the system is found by solving the full set of rate equations which describe the transitions between levels and subsequently used to determine the optical gain. These results can be easily calculated by a moderate PC configuration using the MATLAB programs provided, due to efficient numerical implementation. This is important, since the number of levels involved is inversely proportional to the applied compressible gas.

Acknowledgements

The authors acknowledge support under projetct-PERFU-BOOL02UN070120180007 and support by the research laboratory L.A.R.H.Y.S.S and Laboratory L.M.S.M university of Biskra.

References

1. Tarassov L. Laser physics and applications. MIR publishers, Moscow, Russia. 1984.
2. Svelto O. Principles of lasers. 5^th edition. McGraw-Hill publishers, New York, United States. 1982;431-438
3. O'Shea DC, Callen WR, Rhodes WT. Introduction to lasers and their applications. Addison-Wesley publishers, Massachusetts, United States. 1977;276.
4. Sokol M. Quantum theory of the linewidth of a laser with a saturable absorber: Phase diffusion. Opt Eng. 1998;37(6):1775-1779.

   [Google Scholar]

5. Endo M, Walter RF. Gas lasers. 1^st edition. Taylor and Francis Group, Boca Raton, Florida, United States. 2007;576.
6. Chaouki L, Ferhat M. Modeling the dynamics of the laser oscillation in a nozzle cavity chemical. Int Rev Model Simul. 2014;7(4):740.

   [Crossref]

7. Smiljanic J, Zezelj M, Milanovic V, et al. MATLAB based program for optimization of quantum cascade laser active region parameters and calculation of output characteristics in magnetic field. Comput Phys Commun. 2014;185(3):998-1006.

   [Crossref] [Google Scholar]

8. Miguel JC, Sanjuan AF. The forecast of predictability and instability in physical modelling. ERCIM News. 2010;81.
9. Al-Ajlouni M. An automaic method for creating the profile of supersonic convergent divergent nozzle. Jordan J Mech Ind Eng. 2010;4(3).