Review
, Volume: 6( 1)Model of Nuclear
- *Correspondence:
- Buchakchiiskiy FF, University of St.Gagarin Severodonetsk, Ukraine, Tel: 33662922853; E-mail: ffbuchak@gmail.com
Received: October 03, 2017; Accepted: March 21, 2018; Published: March 28, 2018
Citation: Buchakchiiskiy FF. Model of Nuclear. J Phys Astron. 2018; 6(1):141.
Abstract
It is assumed that basis for formutation of all nuclei is a nucleus of helium. All subsequent nuclei of elements consist of chain of nuclei of helium. They are constrained inter se to binding energy equal energy of separation of nucleus of helium. The chain of nuclei of helium coagulates in a ball.
Keywords
Nuclonous; Helium; Electrolysis; Calcium; Electrode
Introduction
It is known that the number of nuclonous in a nuclei is multiple four plays a large role at determination of properties of nucleus.
Foremost at the nuclei of containing an even number protons and neutrons spin of nucleus equal to the zero. To this group of
elements belong helium 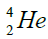 ,carbon
,carbon 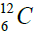 , oxygen
, oxygen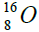 . Because the nucleus of helium
. Because the nucleus of helium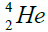 is the simplest, then it serves
as basis for the constriction of all anther nuclei. We will consider the chart of formation of nuclei. We will bild a chart for
calcium. For this purpose we will define the chain of values of energy of separation of nucleus of helium
is the simplest, then it serves
as basis for the constriction of all anther nuclei. We will consider the chart of formation of nuclei. We will bild a chart for
calcium. For this purpose we will define the chain of values of energy of separation of nucleus of helium 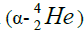 [1-10].
[1-10].
Experimental
Energy of separation 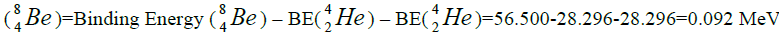
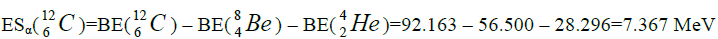
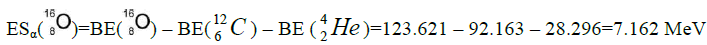
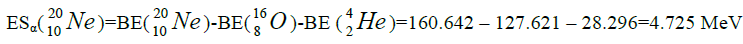
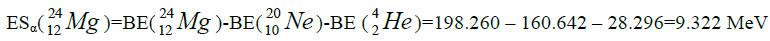
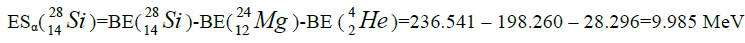
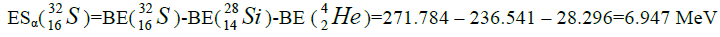
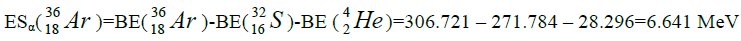
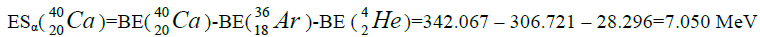
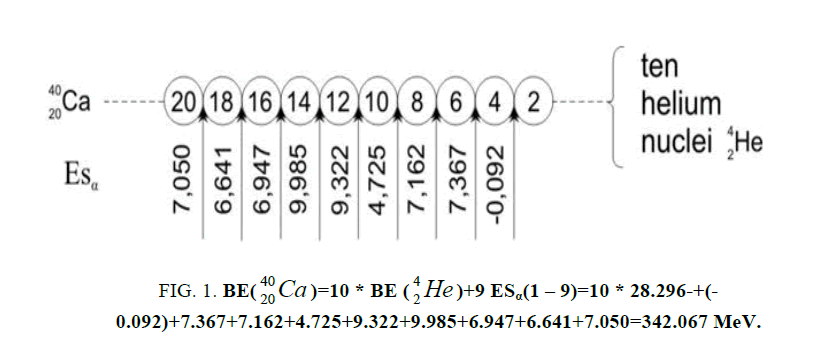
Let us now construct a chain of ten helium nuclei to obtain core the calcium 
Results and Discussion
In table (picture 1) is presented the variant all even nuclei, since the nucleus of helium  , ending uranium
, ending uranium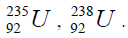
Gonrned, used for the constraction of this table following:
Elements consist of chain of nuclei of helium or isotopes of helium, that enter into co-operation. The value of this cooperation is equal to energy of separation of nucleus of helium or isotope of helium from an element.
This energy links the chain of nuclei.
The constructon of nuclei with even number is begun with nucleus of helium, with an odd number a construction is begun
with deuterium 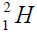 or tritium
or tritium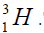 Therefore there are two chains of nuclei.
Therefore there are two chains of nuclei.
In lines the numbers against the name elements stand mass of isotopes.
For example:
Element 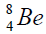 appears from a nucleus of helium addition of another nucleus,
appears from a nucleus of helium addition of another nucleus,
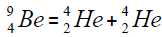
or addition of isotope of helium,
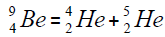
For carbon is brought four isotope 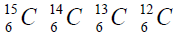
The chart of formation of there isotopes is such,
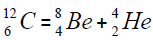
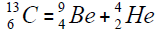
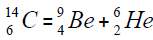
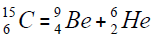
Another example of formation of isotopes of calcium,
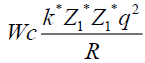
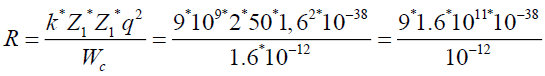
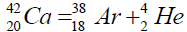
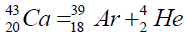
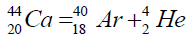
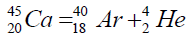
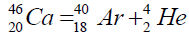
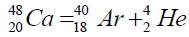
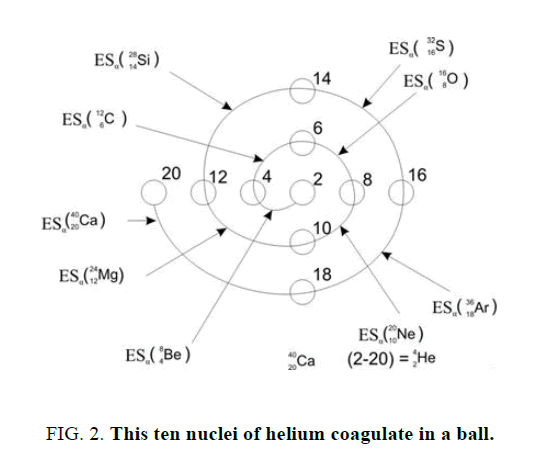
On a picture 2 a chain is presented from the isotope of helium 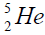 to uranium
to uranium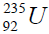 ,This chain is also distinguished in the
table of formation of nucleus (picture 1). Criterion of choice of method of formation of nucleus is a value of energy of
separation of element. We find the value of energy of separation (ESα) for all elements from beryllium
,This chain is also distinguished in the
table of formation of nucleus (picture 1). Criterion of choice of method of formation of nucleus is a value of energy of
separation of element. We find the value of energy of separation (ESα) for all elements from beryllium 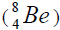 to uranium. If
this value is positive, then of nucleus of helium
to uranium. If
this value is positive, then of nucleus of helium 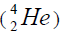 becomes formative, if this value becomes negative then the isotope of
helium
becomes formative, if this value becomes negative then the isotope of
helium 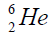 becomes formative.
becomes formative.
In a right side Figures 1-4 the value of energy of separation (ESα) 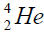 and isotope helium
and isotope helium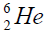 is presented from Coo
responding clements (Table 1).
is presented from Coo
responding clements (Table 1).
Figure 1: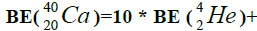 9 ESα(1 – 9)=10 * 28.296-+(-0.092)+7.367+7.162+4.725+9.322+9.985+6.947+6.641+7.050=342.067 MeV.
9 ESα(1 – 9)=10 * 28.296-+(-0.092)+7.367+7.162+4.725+9.322+9.985+6.947+6.641+7.050=342.067 MeV.
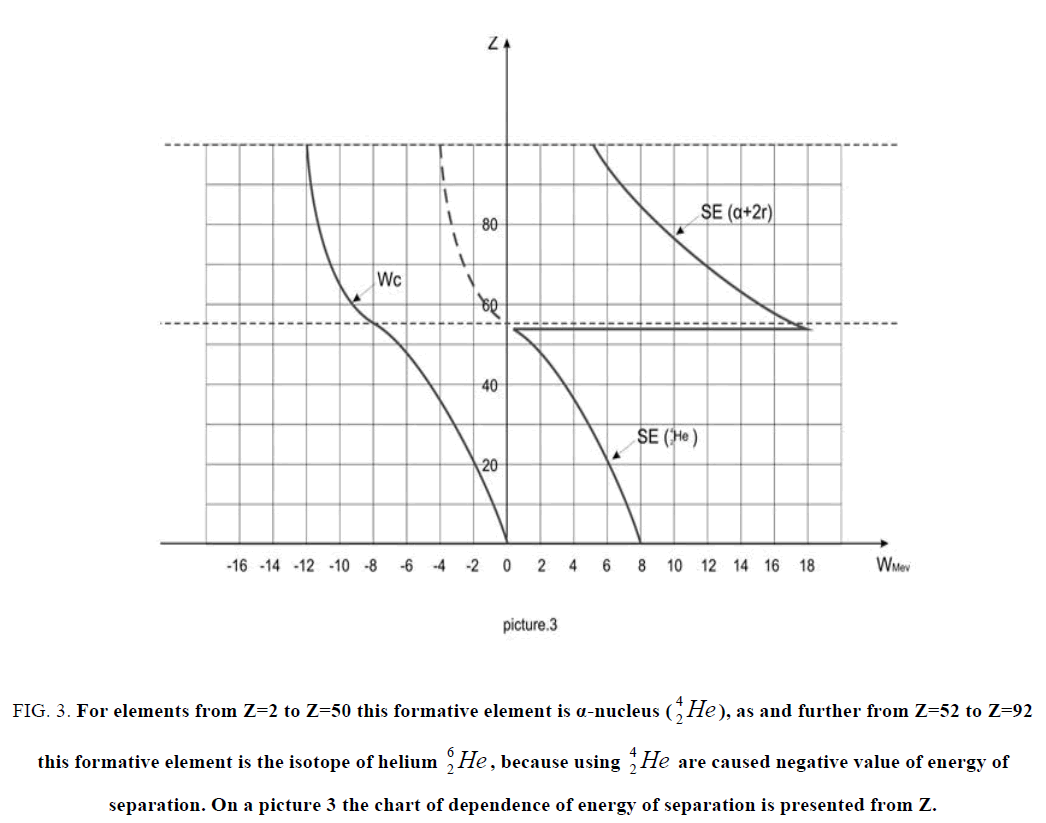
Figure 3: For elements from Z=2 to Z=50 this formative element is α-nucleus as and further from as and further from Z=52 to Z=92 this formative element is the isotope of helium 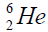 , because using
, because using 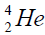 are caused negative value of energy of separation. On a picture 3 the chart
are caused negative value of energy of separation. On a picture 3 the chart 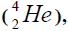 of dependence of energy of separation is presented from Z.
of dependence of energy of separation is presented from Z.
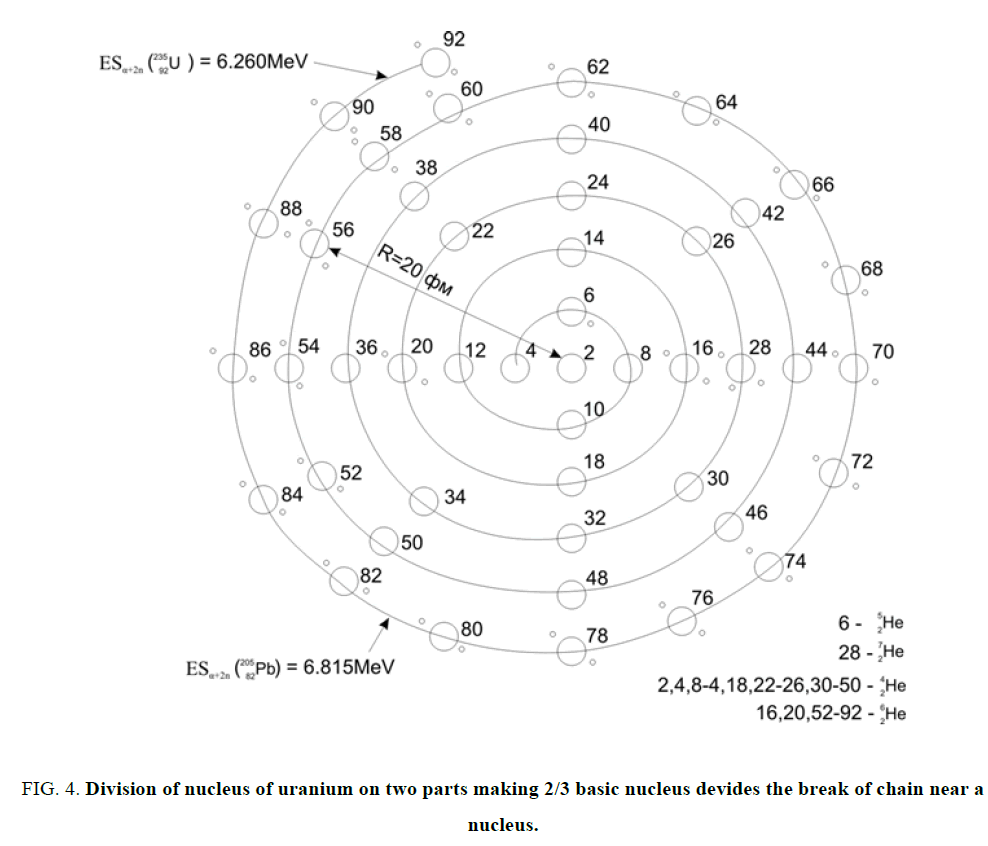
Figure 4: Division of nucleus of uranium on two parts making 2/3 basic nucleus devides the break of chain near a nucleus.
| A | Element | Z | ES α | ES (α+2n) | ES {a+1n} | ES {a+3n} |
|---|---|---|---|---|---|---|
| 5 | He | 2 | ||||
| 9 | Be | 4 | 2.468 | |||
| 14 | C | 6 | 12.011 | 19.716 | ||
| 18 | O | 8 | 6.226 | |||
| 22 | Ne | 10 | 9.668 | |||
| 26 | Mg | 12 | 10.517 | |||
| 30 | Si | 14 | 10.65 | |||
| 36 | S | 16 | 9.009 | 23,820 | ||
| 40 | Ar | 18 | 6.801 | |||
| 46 | Ca | 20 | 11.137 | 25,960 | ||
| 50 | Ti | 22 | 10.717 | |||
| 54 | Cr | 24 | 7.931 | |||
| 58 | Fe | 26 | 7.65 | |||
| 65 | Ni | 28 | 8.634 | 29.163 | ||
| 69 | Zn | 30 | 5.757 | |||
| 73 | Ge | 32 | 5.304 | |||
| 77 | Se | 34 | 5.72 | |||
| 81 | Kr | 36 | 5.52 | |||
| 85 | Sr | 38 | 6.833 | |||
| 89 | Zr | 40 | 6.191 | |||
| 93 | Mo | 42 | 4.301 | |||
| 97 | Ru | 44 | 1.734 | |||
| 101 | Pd | 46 | 1.741 | |||
| 105 | Cd | 48 | 1.357 | |||
| 109 | Sn | 50 | 0.734 | |||
| 115 | Te | 52 | -1.46 | 17.11 | ||
| 121 | Xe | 54 | -0.199 | 18.007 | ||
| 127 | Ba | 56 | -0.009 | 17.938 | ||
| 133 | Ce | 58 | -0.217 | 17.203 | ||
| 139 | Nd | 60 | -0.209 | 17.163 | ||
| 145 | Sm | 62 | -1.115 | 16.262 | ||
| 151 | Gd | 64 | -2.653 | 11.132 | ||
| 157 | Dy | 66 | -1.036 | 13.293 | ||
| 163 | Er | 68 | -1.574 | 13.241 | ||
| 169 | Yb | 70 | -1.733 | 12.791 | ||
| 175 | Hf | 72 | -2.404 | 11.708 | ||
| 181 | W | 74 | 2.211 | 11.266 | ||
| 187 | Os | 76 | -2.724 | 10.56 | ||
| 193 | Pt | 78 | -2.083 | 10.854 | ||
| 199 | Hg | 80 | -0.824 | 12.665 | ||
| 205 | Pb | 82 | -1.465 | 6.815 | ||
| 211 | Po | 84 | -7.534 | 6.258 | ||
| 217 | Rn | 86 | -7.887 | 1.497 | ||
| 223 | Ra | 88 | -5,973 | 3.92 | ||
| 229 | Th | 90 | -5.167 | 5.253 | ||
| 235 | U | 92 | -4,678 | 6.26 |
Table 1: In a right side pictare 2 the value of energy of separation (ESα) and isotope helium is presented from COO responding clements.
Conclusion
Chain of nuclei convolves in a ball. Similar below. Division of nucleus of uranium on two parts making 2/3 basic nucleus devides the break of chain near a nucleus where ESα goes across through a Zero. Placing of the superfluous no included in a?-nuclei neutrons (n=A-2Z).
Appendix

To find a radius, where potential energy of coulomb forces is equal to 10 MeV.
q=l=1,6*10-19 Cl
1 MeV=1,6*10-13 gl
k=9*109
Wc=10 Mev=1.6 *10-12 gl
1 MeV=1,6*10-13 gl
Z1=2 Z2=50|
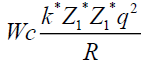
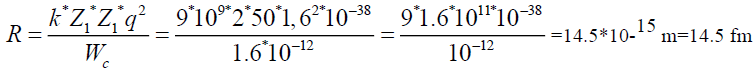
References
- Varlamov VV. Photonuclear Reactions. Modern Status Experimental Data. UDC. 2017;539:12.
- Global National Nuclear Data Center. 2017.
- Centre for Photonuclear Experiments. 2017.
- Kadmensky SG, Kadmensky VG. Cluster degrees of freedom and nuclear reactions and decays cluster phenomena. Atoms and Nuclei. 1992.
- Paolo A. Binuclear Atoms: A model to explain low energy nuclear reactions. J Nuclear Physics. 2017.
- Stoyan SS. Theoretical feasibility of cold fusion according to the BSM. J Nuclear Physics. 2014.
- Richard W. Physics and our universe: How it all works. The Great Courses. USA. 2017.
- Wildermuth K, Tan Y. Unified theory of the nucleus. J Nuclear Physics. 1980.
- Kadmensky SG. Soros Education Magazine. Clusters in Nuclei. 2000;3.
- Chuvilsky YM. Cluster Radioactivity. M Publishing House. 1997;5.