Original Article
, Volume: 15( 1)Left ï -Filters on ï -Semigroups
- *Correspondence:
- Jyothi V , Department of Mathematics, K.L. University, Guntur, Andhra Pradesh, India, Tel:9581423642; E-mail: jyothi.mindspace@gmail.com
Received: February 03, 2017; Accepted: February 23, 2017; Published: March 06, 2017
Citation: Jyothi V, Sarala Y, Madhusudhana Rao D, et al. Left  -Filters on
-Filters on  -Semigroups. Int J Chem Sci. 2017;15(1):104.
-Semigroups. Int J Chem Sci. 2017;15(1):104.
Abstract
In this article we define left -filters, right -filters and prime left -ideal in -semigroup and characterize -semigroups in terms of these notions. Finally, we give the relation between the left -filters and the prime right -ideals
Keywords
Nano powder; Hexagonal wurtzite structure; Chemical precipitation; X-ray diffraction
Introduction
Anjaneyulu [1] initiated the study of ideals in semigroups Petrich [2] made a study on filters in general semigroups. Lee
and Lee [3] introduced the notion of a left filter in a PO semigroup. Kehayopulu [4-6] gave the characterization of the
filters of S in terms of prime ideals in ordered semigroups [7-9]. Sen [10] introduced  -semigroups in 1981. Saha [11]
introduced
-semigroups in 1981. Saha [11]
introduced  -semigroups different from the first definition of
-semigroups different from the first definition of  -semigroups in the sense of sen.
-semigroups in the sense of sen.
Let S and  be two nonempty sets. Then S is said to be a
be two nonempty sets. Then S is said to be a  -semigroup if there exist a mapping from SX
-semigroup if there exist a mapping from SX XS →S
which maps (a,α,b)→aαb satisfying the condition
XS →S
which maps (a,α,b)→aαb satisfying the condition 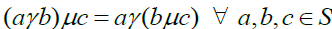 and
and 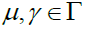 [8].
[8].
Let S be a  -semigroup. If A and B are two subsets of S, we shall denote the set
-semigroup. If A and B are two subsets of S, we shall denote the set 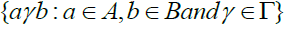 by A
by A B.
B.
Let S be a  - semigroup. A non-empty subset A of S is called a right
- semigroup. A non-empty subset A of S is called a right  -ideal of S if
-ideal of S if 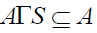 . A non empty subset
A of a
. A non empty subset
A of a  -semigroup S is a right
-semigroup S is a right  -ideal of S if
-ideal of S if 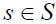 ,
,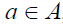 ,
, 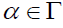 implies
implies 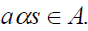 [8].
[8].
Let S be a  -semigroup. A non empty A of S is called a left
-semigroup. A non empty A of S is called a left  -ideal of S if
-ideal of S if 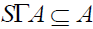 . A nonempty subset A of
a
. A nonempty subset A of
a  -semigroup S is a right
-semigroup S is a right  -ideal of S if
-ideal of S if 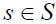 ,
, 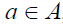 ,
, 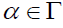 implies
implies 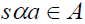 . A is called an
. A is called an  -ideal of S
if it is a right and left
-ideal of S
if it is a right and left  -ideal of S.
-ideal of S.
A subset T of S is called a prime if 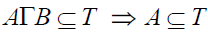 or
or 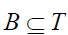 for subsets A,B of S. T is called a prime
right ideal if T is prime as a right ideal. T is called a prime left ideal if T is a prime as a left ideal. T is called a prime
ideal if T is prime as an ideal [11].
for subsets A,B of S. T is called a prime
right ideal if T is prime as a right ideal. T is called a prime left ideal if T is a prime as a left ideal. T is called a prime
ideal if T is prime as an ideal [11].
We now introduce the left  -filter, right
-filter, right  -filter and
-filter and  -filter.
-filter.
A  -sub semigroup F of a
-sub semigroup F of a  -semigroup S is called a left
-semigroup S is called a left  -filter of S if
-filter of S if 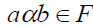 for
for
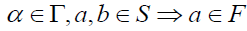 . A
. A  -semigroup F of a
-semigroup F of a  -semigroup S is called a right
-semigroup S is called a right  -filter of S if
-filter of S if 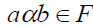 for
for
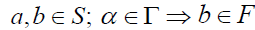 . [13].
. [13].
Theorem (1)
Let S be a  -semigroup and F a non-empty subset of S. The following are equivalent.
-semigroup and F a non-empty subset of S. The following are equivalent.
1. F is a left  -filter of S.
-filter of S.
2. S \ F = 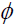 or S \ F is a prime right
or S \ F is a prime right  -ideal.
-ideal.
Proof: (1)⇒(2) : Suppose that S \ F # 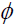 . Let x∈S \ F;α∈
. Let x∈S \ F;α∈ and y∈S . Then xαy∈S \ F . Indeed: If
xαy
and y∈S . Then xαy∈S \ F . Indeed: If
xαy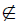 S \ F ; then xαy∈F. Since F is a left
S \ F ; then xαy∈F. Since F is a left  -filter, x∈F. It is impossible. Thus xαy∈S \ F, and so
(S \ F)
-filter, x∈F. It is impossible. Thus xαy∈S \ F, and so
(S \ F) S ⊆ S \ F. Therefore S \ F is a
S ⊆ S \ F. Therefore S \ F is a  right ideal.
right ideal.
Next, we shall prove that S \ F is a prime.
Let xαy∈S \ F for x, y ∈ S and α∈ . Suppose that x
. Suppose that x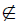 S \ F and y
S \ F and y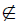 S \ F. Then x∈F and y∈F. Since
F is a sub semigroup of S , xαy∈F. It is impossible. Thus x∈S \ F or y∈S \ F. Hence S \ F is a prime, and so
S \ F is a prime right
S \ F. Then x∈F and y∈F. Since
F is a sub semigroup of S , xαy∈F. It is impossible. Thus x∈S \ F or y∈S \ F. Hence S \ F is a prime, and so
S \ F is a prime right  - ideal.
- ideal.
(2)⇒(1) : If S \ F = 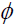 then F = S. Thus F is a left -filter of S. Next assume that S \ F is a prime right
then F = S. Thus F is a left -filter of S. Next assume that S \ F is a prime right  -
ideal of S. Then F is a
-
ideal of S. Then F is a  -sub semigroup of S. Indeed: Suppose that xαy
-sub semigroup of S. Indeed: Suppose that xαy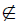 F for x, y∈F and α∈
F for x, y∈F and α∈ . Then xαy∈S \ F for x, y∈F and α∈
. Then xαy∈S \ F for x, y∈F and α∈ . Since S \ F is prime, x, y∈S \ F. It is impossible. Thus xαy∈F and so F is a sub semigroup of S.
. Since S \ F is prime, x, y∈S \ F. It is impossible. Thus xαy∈F and so F is a sub semigroup of S.
Let xαy∈F for x, y∈S and α∈ . Then x∈F. Indeed: If x
. Then x∈F. Indeed: If x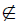 F, then x∈S \ F. Since S \ F is a prime
right
F, then x∈S \ F. Since S \ F is a prime
right  -ideal of S, xαy∈(S \ F)
-ideal of S, xαy∈(S \ F) S ⊆ S \ F. It is impossible. Thus x∈F. Therefore F is a left filter of S.
S ⊆ S \ F. It is impossible. Thus x∈F. Therefore F is a left filter of S.
Theorem (2)
Let S be a  -semigroup and F be a non-empty subset of S. The following are equivalent.
-semigroup and F be a non-empty subset of S. The following are equivalent.
(1) F is a right  filter of S.
filter of S.
(2) S \ F =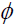 or S \ F is a prime left
or S \ F is a prime left  -ideal.
-ideal.
Proof: (1)⇒(2) :Suppose that S \ F =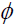 . Let y∈S \ F; α∈
. Let y∈S \ F; α∈ and y∈S. Then xαy∈S \ F. Indeed: If
xαy∈S \ F; then xαy∈F. Since F is a right
and y∈S. Then xαy∈S \ F. Indeed: If
xαy∈S \ F; then xαy∈F. Since F is a right  -filter, y∈F. It is impossible. Thus xαy∈S \ F, and so
S
-filter, y∈F. It is impossible. Thus xαy∈S \ F, and so
S (S \ F) ⊆ S \ F. Therefore S \ F is a left
(S \ F) ⊆ S \ F. Therefore S \ F is a left  -ideal.
-ideal.
Next, we shall prove that S \ F is a prime.
Let xαy∈S \ F for x, y∈S and α∈ . Suppose that x
. Suppose that x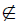 S \ F and y
S \ F and y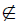 S \ F. Then x∈F and y∈F.
Since F is a sub semigroup of S, xαy∈F. It is impossible. Thus x∈S \ F or y∈S \ F. Hence S \ F is a prime
and so that S \ F is a prime left
S \ F. Then x∈F and y∈F.
Since F is a sub semigroup of S, xαy∈F. It is impossible. Thus x∈S \ F or y∈S \ F. Hence S \ F is a prime
and so that S \ F is a prime left  -ideal.
-ideal.
(2)⇒(1) : If S \ F =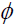 then S = F . Thus F is a right
then S = F . Thus F is a right  -filter of S. Next assume that S \ F is a prime left
-filter of S. Next assume that S \ F is a prime left  -
ideal of S. Then F is a
-
ideal of S. Then F is a  -sub semigroup of S. Indeed: Suppose that for x, y∈F and α∈
-sub semigroup of S. Indeed: Suppose that for x, y∈F and α∈ . Then xαy∈S \ F
for x, y∈F and α∈
. Then xαy∈S \ F
for x, y∈F and α∈ . Since S \ F is a prime, x, y∈S \ F. It is impossible. Thus xαy∈F; α∈
. Since S \ F is a prime, x, y∈S \ F. It is impossible. Thus xαy∈F; α∈ and so F
is a
and so F
is a  sub semigroup of S.
sub semigroup of S.
Let xαy∈F for x, y∈S and α∈ . Then yF. Indeed: If y
. Then yF. Indeed: If y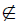 F, then y∈S \ F. Since S \ F is a prime
right
F, then y∈S \ F. Since S \ F is a prime
right  ideal of S, xαy ∈ S
ideal of S, xαy ∈ S (S \ F) S \ F. It is impossible. Thus y∈F. Therefore F is a right
(S \ F) S \ F. It is impossible. Thus y∈F. Therefore F is a right  filter of S.
From theorem 2.6 and 2.7, we get the following.
filter of S.
From theorem 2.6 and 2.7, we get the following.
Corollary: Let S be a  -semigroup and F be a non-empty subset of S. The following are equivalent.
-semigroup and F be a non-empty subset of S. The following are equivalent.
(1) F is a  filter of S.
filter of S.
(2) S \ F =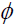 or S \ F is a prime
or S \ F is a prime  -ideal of S.
-ideal of S.
Proof: (1)⇒(2) : Assume that S \ F =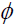 .
.
By theorem (1), S \ F is a right  ideal.
ideal.
By theorem (2), S \ F is a left  ideal.
ideal.
By theorem (1) and (2), S \ F is a  ideal.
ideal.
By theorem (2) and (2), S \ F is a prime  ideal of S.
ideal of S.
(2)⇒(1) : If S \ F =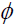 then F = S. Thus F is a
then F = S. Thus F is a  -filter of S. Next assume that S \ F is a prime
-filter of S. Next assume that S \ F is a prime  -ideal of
S. By theorem (1) and (2). F is a
-ideal of
S. By theorem (1) and (2). F is a  -subsemigroup of S. Let xαy ∈F for x, y∈S and α∈
-subsemigroup of S. Let xαy ∈F for x, y∈S and α∈ . By theorem (1);
F is a left
. By theorem (1);
F is a left  -filter of S. By theorem (2); F is a right
-filter of S. By theorem (2); F is a right  -filter of S. Therefore F is a
-filter of S. Therefore F is a  -filter of S.
-filter of S.
Conclusion
This concept is used in filters of chemistry, physical chemistry, electronics.
References
- AnjeaneyuluA. Structure and ideal theory of semigroups, thesis,ANU. 1980.
- Petrich M. The introduction to semigroups. Merrill Publishing Company, Columbus, Ohio. 1973.
- Lee SK, Kwon YI. ?On left regular po-semigroups?, Comm. Korean Math Soc. 1998;13:1-6.
- KehayopuluN.On filters generalized in po-semigroups.MathJapan.1990;35:789-96.
- KehayopuluN.Remark on ordered semigroups.MathJapan.1990;35:1061-63.
- Kehayopulu N.On left regular orderedsemigroups. MathJapan.1990;35:1057-60.
- LeeSK,Kwon YI. ?On left regular po-semigroups?, Comm. Korean Math Soc.1998;13:1-6.
- Madhusudhana RaoD, Anjaneyulu A,Gangadhara RaoA. Prime-radicals in semigroups. Inte-j math Eng. 2011; 116:1074-81.
- Clifford AH, Preston GB. The algebraic theory of semigroups. Am math soc Providence II. 1967.
- Sen MK.On-semigroups. Proceeding of international Conference of Algebra and its Application, Decker publication, New York-301.
- Saha NK. On-semigroups-III. BullCulMathSoc.1988;116:1-12.
