Original Article
, Volume: 11( 4) DOI: 10.37532/2320-6756.2023.11(4).335Flyby Radio Doppler and Ranging Data Anomalies are due to different inbound and outbound velocities in the CMB rest frame
Received date: 18-February-2023, Manuscript No. tspa-23-89620; Editor assigned: 22-February-2023, Pre-QC No. tspa-23-89620 (PQ); Reviewed: 15-March-2023, QC No. tspa-23-89620 (Q); Revised: 22-March-2023, Manuscript No. tspa-23-89620 (R); Published: 25-April-2023, DOI. 10.37532/2320-6756.2023.11(4).335
Citation: Pabisch R. Flyby Radio Doppler and Ranging Data Anomalies are due to Different Inbound and Outbound Velocities in the CMB Rest Frame. J. Phys. Astron.2023;11(4):335.
Abstract
The COBE, WMAP, and Planck data analyses exhibit that the CMB rest frame can be seen as a fundamental, absolute space, the CMBspace. All Earth flyby radio Doppler data anomalies can be resolved by applying the general, classical Doppler formula (CMB-Doppler formula) of first order for two-way signals between earthbound Deep Space Network stations and a spacecraft during an Earth flyby. For that purpose, the annually varying absolute velocity vector ue of Earth is used, derived from the absolute velocity vector of the solar system barycenter, usun magnitude 1 369.82 0.11 sun u kmsï€Â  , in direction of constellation Crater, near Leo. Together with the relative,asymptotic inbound and outbound velocity vectors inv and outv in the equatorial frame, we obtain the absolute inbound and outbound velocity vectors uin and uout in the equatorial frame. The relative, asymptotic inbound and outbound velocities are actually equal in magnitude( ) in out v  v , while the magnitudes of the absolute inbound and outbound velocities of a spacecraft are in general different ( ) in out u  u , leading to the apparent anomaly. Thus the use of the CMB-Doppler formula explains the so far as residual considered positive or negative differences in energy. The measured, different absolute velocities in the CMB rest frame explain the supposed radar ranging data residuals as well.
Keywords
Earth flyby anomalies; Absolute velocities in the CMB rest frame; General classical Doppler formula of first and second order in the CMB rest frame
Theoretically Derived Formula is Reproducing the Empirically Devised Prediction Formula
The flyby anomalies, which in most cases show an apparent acceleration, some null results and one significant deceleration between the inbound and outbound flights, are still unexplained [1, 2]. The total geocentric orbital energy per unit mass should be the same before and after the flyby at infinity. The data indicate this is not always true.
To predict further flyby anomalies, 15 years ago (Anderson & Campell & Ekelund, 2008) published an empirically devised formula from previous flyby anomaly data, which involves the incoming and outgoing geocentric latitudes of the relative, asymptotic velocity vectors [1],

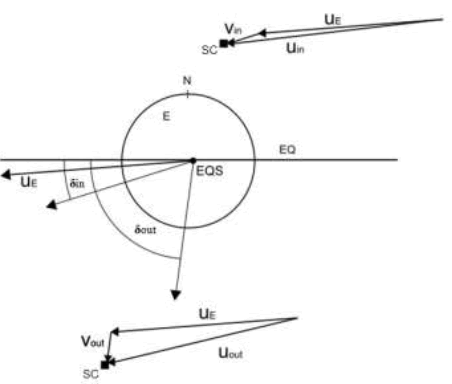
where ΔV∞ is the apparent anomalous difference in velocity, V∞ is the asymptotic relative velocity, δin is the asymptotic, geocentric latitude of the inward flight trajectory, δout is the asymptotic, geocentric latitude of the outward flight trajectory, and K has the constant value 3.099×10-6 . Using the CMB-Doppler formula approach for two-way tracking signals (see formulas (2) and (3)), we obtain KCMB = 3.059 [3]. Obviously, the ranging data anomaly is also caused by the different absolute velocities of the inbound and outbound flights, see FIG. 1, and again the CMB-approach will explain accelerations, decelerations and null results as well.
Figure 1: Schematic visualization of the absolute velocity vector  of Earth and the relative, asymptotic pre-encounter
velocity vector
of Earth and the relative, asymptotic pre-encounter
velocity vector 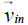 , the relative, asymptotic post-encounter velocity vector
, the relative, asymptotic post-encounter velocity vector 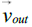 of a Spacecraft (SC) in the Equatorial
Frame (EQS), their declination angles δin and δout, the derived absolute asymptotic pre-encounter and postencounter
velocity vectors
of a Spacecraft (SC) in the Equatorial
Frame (EQS), their declination angles δin and δout, the derived absolute asymptotic pre-encounter and postencounter
velocity vectors 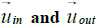 of a spacecraft during a gravity assisted flyby manoeuvre.
of a spacecraft during a gravity assisted flyby manoeuvre.
The latest Planck dipole data analyses Planck Collaboration I indicate a peculiar velocity of the solar system of 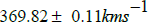 in direction of constellation Crater near Leo, at
in direction of constellation Crater near Leo, at 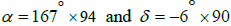 . The absolute velocity of Earth in the CMB rest frame varies between
ue =
340kms-1 around mid-June and
ue =
400kms-1 around mid-December during the yearly revolution, while
the velocity at mid-March or mid-September is
ue =
371kms-1 . From that velocity the value
KCMB = 3.059 10-6 follows, if the
CMB-space approach is applied, see formula (9).
. The absolute velocity of Earth in the CMB rest frame varies between
ue =
340kms-1 around mid-June and
ue =
400kms-1 around mid-December during the yearly revolution, while
the velocity at mid-March or mid-September is
ue =
371kms-1 . From that velocity the value
KCMB = 3.059 10-6 follows, if the
CMB-space approach is applied, see formula (9).
We now assert, that calculating the frequencies of two way signals between any two moving bodies in the universe, especially in the
solar system, the CMB-Doppler formula of first order in the absolute space of the CMB rest frame has to be applied, instead of the
relativistic Doppler formula of first order. The absolute velocity  of a Spacecraft (SC) is derived by addition of its relative velocity
of a Spacecraft (SC) is derived by addition of its relative velocity  in the geocentric frame together with the absolute velocity
in the geocentric frame together with the absolute velocity 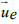 of Earth, see FIG. 1. The absolute velocity
of Earth, see FIG. 1. The absolute velocity 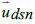 of the Deep
Space Network stations (DSN) is calculated by adding its rotational velocity in the geocentric frame and the absolute velocity
of the Deep
Space Network stations (DSN) is calculated by adding its rotational velocity in the geocentric frame and the absolute velocity 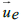 of
Earth. We neglect the rotational velocity in our formula for simplicity because of the minimal effect, hence
of
Earth. We neglect the rotational velocity in our formula for simplicity because of the minimal effect, hence 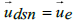 . The time
dilatation effect as a function of absolute velocities in the CMB rest frame is neglected too, for reasons we discussed in Pabisch &
Kern, and in a more recent paper [4, 5, 6]. All vectors are defined in the equatorial frame of Earth.
. The time
dilatation effect as a function of absolute velocities in the CMB rest frame is neglected too, for reasons we discussed in Pabisch &
Kern, and in a more recent paper [4, 5, 6]. All vectors are defined in the equatorial frame of Earth.
The CMB-Doppler formula of first order for an uplink signal reads,

where fdsn denotes the frequency of the uplink signal emitted by a DSN station,
f'sc the frequency of the uplink signal received
and measured by a spacecraft SC, c the constant velocity of light in the CMB rest frame, α1 the angle between the vector  and the vector
and the vector  of the uplink signal,
α2 the angle between the vector
of the uplink signal,
α2 the angle between the vector 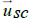 and the vector
and the vector  of the downlink signal.
of the downlink signal.
The CMB-Doppler formula of first order for a downlink signal reads,

where 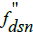 denotes the frequency of the downlink signal, as received and measured by a DSN station.
denotes the frequency of the downlink signal, as received and measured by a DSN station.
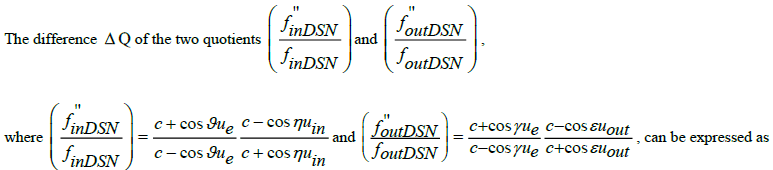
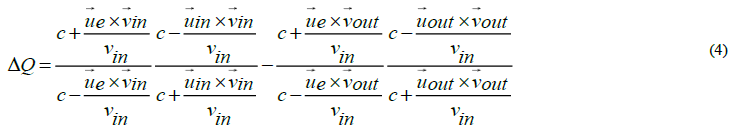
We assume that in the geocentric frame the condition vin = vout at infinity is valid, despite the apparent flyby anomaly, and the relative and absolute velocity vectors of formula (4) are defined as,

is the relative, asymptotic velocity vector of the incoming spacecraft, as calculated in the equatorial frame,
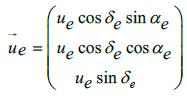
is the absolute velocity vector of Earth in the equatorial frame,
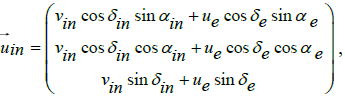
where  is the absolute, asymptotic velocity vector of the incoming spacecraft in the equatorial frame,
is the absolute, asymptotic velocity vector of the incoming spacecraft in the equatorial frame,
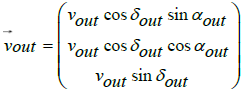
is the relative, asymptotic velocity vector of the outgoing spacecraft, as calculated in the equatorial frame, and
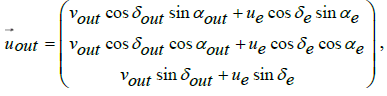
where 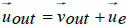 is the absolute, asymptotic velocity vector of the outgoing spacecraft in the equatorial frame.
is the absolute, asymptotic velocity vector of the outgoing spacecraft in the equatorial frame.
Each of these vectors is defined in the equatorial frame of Earth by means of its declination δ and right ascension α and its
magnitude relative to the center of Earth. Furthermore ϑ is the angle between the absolute velocity vector 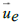 of the geocentric, and
the relative, asymptotic velocity vector
of the geocentric, and
the relative, asymptotic velocity vector  of the incoming spacecraft, as calculated in the equatorial frame,
of the incoming spacecraft, as calculated in the equatorial frame,
where

γ denotes the angle between the absolute velocity vector 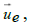 , and the relative, asymptotic velocity vector
, and the relative, asymptotic velocity vector  of the outgoing
spacecraft in the equatorial frame,
of the outgoing
spacecraft in the equatorial frame,
where 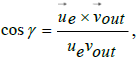
ε denotes the angle between the absolute, asymptotic velocity vector 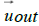 of the outgoing spacecraft, and the relative, asymptotic
velocity vector
of the outgoing spacecraft, and the relative, asymptotic
velocity vector 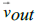 of the outgoing spacecraft in the equatorial frame,
of the outgoing spacecraft in the equatorial frame,
From formula (4) we now obtain formula (5),
where 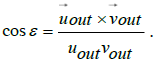
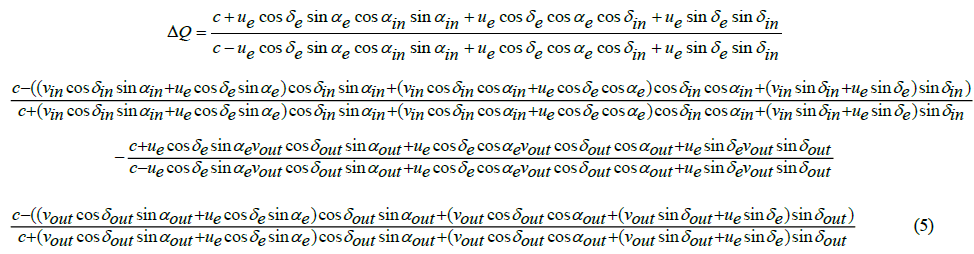
Since the asymptotic inward flight right ascension angle αin, and the asymptotic outward flight right ascension angle αout do have a negligible effect on the quotient ΔQ of αin formula (5), we approximate further, and by equating αin = αout=αe =δe we obtain with
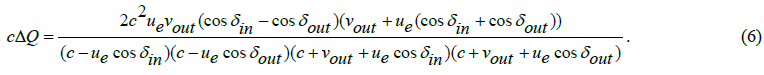
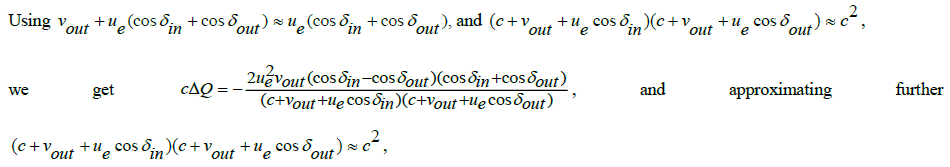
we obtain,
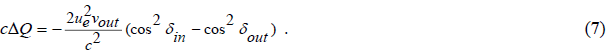
If we consider 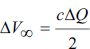 as difference in velocity, we get,
as difference in velocity, we get,
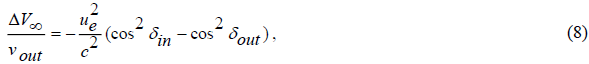
and finally,
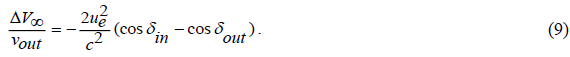
The term 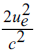 yields 3.059×10-6 for the factor KCMB , if the velocity of Earth
ue = udsn = 371kms-1 around mid-March is inserted.
Due to the CMB-approach, the value of 3.059×10-6 is not constant, but varies as a consequence of the annual variation of the absolute
velocity of Earth between
ue = 340kms-1 and
ue = 400kms-1 . Around mid-June
KCMB = 2.57× 10-6 results, and around mid-
December
KCMB = 3.55 × 10-6 . The negative sign of our factor KCMB stems from the difference of the absolute inbound velocity
minus absolute outbound velocity as can be seen in formula (4). The other way around a positive value results.
yields 3.059×10-6 for the factor KCMB , if the velocity of Earth
ue = udsn = 371kms-1 around mid-March is inserted.
Due to the CMB-approach, the value of 3.059×10-6 is not constant, but varies as a consequence of the annual variation of the absolute
velocity of Earth between
ue = 340kms-1 and
ue = 400kms-1 . Around mid-June
KCMB = 2.57× 10-6 results, and around mid-
December
KCMB = 3.55 × 10-6 . The negative sign of our factor KCMB stems from the difference of the absolute inbound velocity
minus absolute outbound velocity as can be seen in formula (4). The other way around a positive value results.
Cahill derived a formula on equivalent theoretical reasoning. He asserted, that the speed of light is not invariant, and is isotropic only with respect to the CMB rest frame [7]. For some reason he then applies a shibboleth absolute velocity of the solar system to calculate the flyby effects, which deviates significantly in direction and magnitude from the latest Planck values.
Note that the formula by Anderson et al., and hence our theoretically derived formula as well, gives wrong, not null anomaly predictions for the second and third Rosetta flybys, and for the Juno flyby of October 2013, [1, 2]. A deviation sometimes arises when the inbound frequency, in fact due to the absolute inbound velocity uin , leads to a misleading value of the relative inbound velocity vin , which results from the standard Doppler formula of first order and the varying factor KCMB may be a reason, too. The difference between the inbound angles of the relativistic Doppler formula and the CMB-Doppler formula should not be overlooked also, see FIG. 1.
Predictions
The dipole Doppler term of 1st order is the result of the motion of our solar system through space. It is a frame dependent quantity, and we can determine the absolute rest frame as that in which the dipole would be zero. We conclude from formula (9), and the resulting factor KCMB , that the use of the CMB-Doppler formulas does yield frequencies which will match all measured positive or negative deviations during Earth flyby maneuvers, despite vin = vout is valid in the geocentric frame. A renewed evaluation of the correspondently observed ranging data, using the magnitudes of the absolute, asymptotic inbound and outbound velocity vectors, and of the absolute velocity vector of Earth will exhibit velocity differences which explain the seemingly anomalies, measured during some flyby man oeuvres. Several other successful applications of the CMB approach make a random match of formula (9) with the empirically found formula (1) vastly improbable.
The motion of an observer with velocity v relative to the isotropic Planckian radiation field produces a temperature pattern of [10, 11],

Formula (10) is written in most publications,
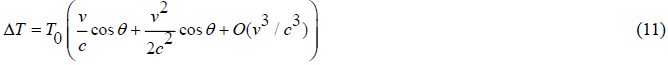
Thus hiding the effect of time dilatation in CMB-space, often described as Doppler Effect of 2nd order which is a function of velocity
too, but a quite different physical effect compared to the 1st order effect. The value of the quadratic term of the CMB dipole formula
(10), the inverse γ-Factor, precisely confirms the purely kinematic origin of the first order effect. That concordance indicates we have
to interpret the time dilatation effect as an asymmetric function of absolute velocities u in the CMB rest frame [5]. Due to ve = vu in formula (10) and (11), Earth Eigen time is obviously not invariant since it varies annually 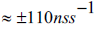 around a time dilatation
value of
765nss-1 at mid-March or mid-September. Clocks at Earth are delayed less than one microsecond per second versus a clock
at rest in the CMB-rest frame, the SI-second is not invariant. Only against the absolute temperature variations, due to the absolute
motion of Earth that asymmetric effect can be measured, not within any laboratory on Earth, at least until now [12].
around a time dilatation
value of
765nss-1 at mid-March or mid-September. Clocks at Earth are delayed less than one microsecond per second versus a clock
at rest in the CMB-rest frame, the SI-second is not invariant. Only against the absolute temperature variations, due to the absolute
motion of Earth that asymmetric effect can be measured, not within any laboratory on Earth, at least until now [12].
The CMB Doppler formulas of 1st order not only allow to calculate the, in general slightly different, absolute inbound and outbound velocities of flyby man oeuvres, thus resolving the flyby anomalies. The quite different phenomenon of the annual and diurnal signal residuals on top of the resolved Pioneer 10 acceleration term is as well resolved by applying the CMB Doppler formula of 1st order [6,8, 9].
The CMB multipole anomaly is resolved in CMB-space as well. The observed alignment of the low multipoles (quadrupole and octopole) with one another and their perpendicular orientation to the Ecliptic is not a mysterious property of the presumptive background radiation [13-15]. That in standard physics unexplained phenomenon is caused by the annual motion of Earth, and the fortunate random fact, that the absolute vector of the solar systems velocity runs nearly parallel to the ecliptic, near to the equinoxes. Summarizing, we have several independent indications that the CMB-space approach is new physics:
• We can measure absolute velocities and absolute directions of bodies, stars and galaxies, at least in our cosmic neighborhood.
• The application of the classical Doppler formula of 1st order in the CMB-space (CMB Doppler formula) resolves several different, so far unexplained deviations from the standard Doppler formula of 1st order.
• Absolute velocities of bodies cause physical effects like time dilatation. That supports the assumption of an inertial mass of photons [5], [6].
• The solar system is not cosmically aligned, as argued in [13-15], and the CMB anomaly of the north-south hemispheric asymmetry, the preference of odd parity, and the cold spot are all resolved in an anisotropic and inhomogeneous cosmos.
Conclusion
We predict, the forthcoming data and images from the James Webb Space Telescope (JWST) will show that the expected structures and traces of an infant universe, according to the ΛCDM model are not to find in the outermost regions. Instead, at least some massive galaxies and quasars will show up in the data. Possibly the region beyond a distance of 13.7 billion years is not the assumed edge of our Universe. The presumptive age of our cosmos of 13.8 billion years is challenged, just a several other components of the ΛCDM model. The particular reasons, supporting those predictions, will follow in another publication.
References
- Anderson JD, Campbell JK, Ekelund JE, et al. Anomalous orbital-energy changes observed during spacecraft flybys of Earth. Phys. Rev. Lett. 2008;100(9):091102.
- Acedo L. The flyby anomaly: a multivariate analysis approach. Astrophys. Space Sci. 2017;362(2):42.
[Google Scholar] [Crossref]
- Pabisch R., Kern Ch. Verfahren zur Verbesserung der Steuerungsgenauigkeit einer Raumsonde im Sonnensystem. Deutsches Patent- und Markenamt, DE 10 2010 054741 A1; 2010 [Google Scholar] [Crossref]
- Aghanim N, Akrami Y, Arroja F, et al. Planck 2018 results-I. Overview and the cosmological legacy of Planck. Astron. Astrophys. 2020;641:A1.
- Pabisch R. Derivation of the time dilatation effect from fundamental properties of photons. Springer-Verlag Wien New York, Linzer Universit¨atsschriften. 1999;ISBN 3-211-83153-3 [Google Scholar] [Crossref]
- Pabisch R.,Residual annual and diurnal periodicities of the Pioneer 10 acceleration term resolved in absolute CMB rest frame. viXra:1806.0389v1. Astrophysics, 2018 [Google Scholar] [Crossref]
- Cahill RT. Resolving spacecraft Earth-flyby anomalies with measured light speed anisotropy. Prog. Phys. 2008;3(6):9-15.
[Google Scholar] [Crossref]
- Anderson JD, Laing PA, Lau EL, et al. Study of the anomalous acceleration of Pioneer 10 and 11. Phys. Rev. D. 2002;65(8):082004.
- Rievers B, Lämmerzahl C. High precision thermal modeling of complex systems with application to the flyby and Pioneer anomaly. Annalen der Physik. 2011;523(6):439-49.
- Adam R, Ade PA, Aghanim N, et al. Planck 2015 results-VIII. High Frequency Instrument data processing: Calibration and maps. Astron. Astrophys. 2016;594:A8.
- D. Scott, G.F. Smoot 29. Cosmic Microwave Background, 2019. [Google Scholar] [Crossref]
- Sanner C, Huntemann N, Lange R, et al. Optical clock comparison for Lorentz symmetry testing. Nature. 2019;567(7747):204-8.
[Google Scholar] [Crossref]
- Schwarz DJ, Copi CJ, Huterer D, et al. CMB anomalies after Planck. Class. Quantum Gravity. 2016;33(18):184001.
- Schwarz D.J, Starkman G.D, Huterer D, et al. Is the low-l Microwave Background Cosmic? Phys. Rev. Lett. 2004.[Google Scholar]
[Crossref]
- Huterer D. Why is the solar system cosmically aligned?.2007 [Google Scholar] [Crossref]