+44 7362 049930
Original Article
, Volume: 15( 4)Elzaki Transform for Two Tank Mixing Problems
- *Correspondence:
- Naresh P, Faculty of Mathematics, Department of Science and Humanities, Sreenidhi Institute of Science and Technology, Ghatkesar, Hyderabad, Telangana, India, Tel: 9959525584; E-mail: parakala2@gmail.com
Received: September 06, 2017; Accepted: October 16, 2017; Published: October 23, 2017
Citation: Naresh P, Umamaheshwar Rao R, Eswarlal T. Elzaki Transform for Two Tank Mixing Problems. Int J Chem Sci. 2017;15(4):205
Abstract
Integral transform method is a powerful method which is widely used to solve the several kinds of differential equations with initial or boundary conditions. The new integral transform method called as Elzaki transform method is useful for solving differential equations, integro-differential equations and also integral equations. This method is also useful for solving nonlinear differential equations; it also provides an effective and efficient way of solving a wide range of problems. In this paper, we have used the Elzaki transform method for solving the two tank mixing problems, which was an application of first order system of linear differential equation.
Keywords
Elzaki transform; Differential equations
Introduction
In science and engineering differential equations plays an important role. In order to solve the differential equations, the integral transforms were extensively used. The importance of an Integral Transforms is that they provide powerful operational methods for solving initial value problems. Mostly we use Laplace Transform technique for solving differential equations. Elzaki Transform is the new integral transform which is stronger than Sumudu and Laplace Transforms.
Elzaki Transform was introduced by Tarig Elzaki [1] in 2011. Elzaki Transform defined for function of exponential order, we
consider function on the set A defined by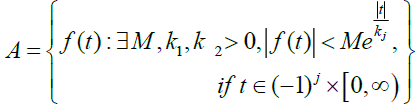 
For a given function in the set A
the constant M must be a finite number, k1 and k2 may be finite or infinite.
The Elzaki transform is defined by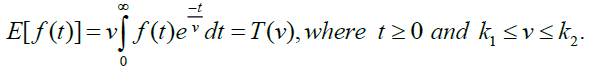 
The sufficient conditions for the existence of the Elzaki transform are that f (t) for t ≥ 0 be piecewise continuous and of the exponential order otherwise Elzaki transform may (or) may not exist [2].
Experimental
Elzaki transform of some functions and for first derivate
Here we consider some standard functions and the first derivative which are mostly occurred in the problems on Newton’s law cooling; their Elzaki transforms are given below.
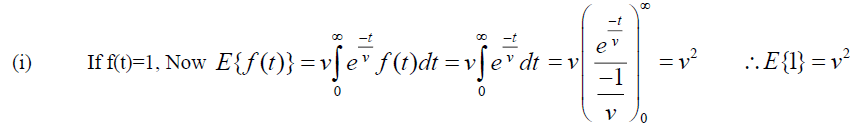
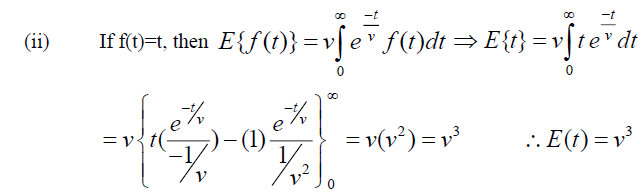
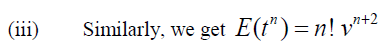
Theorem (1): Let f (t) be the given function and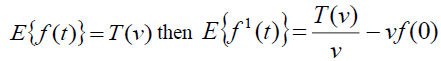 
Proof: Given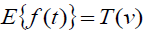 
, By Definition of Elzaki Transform
.
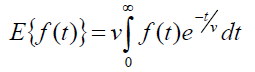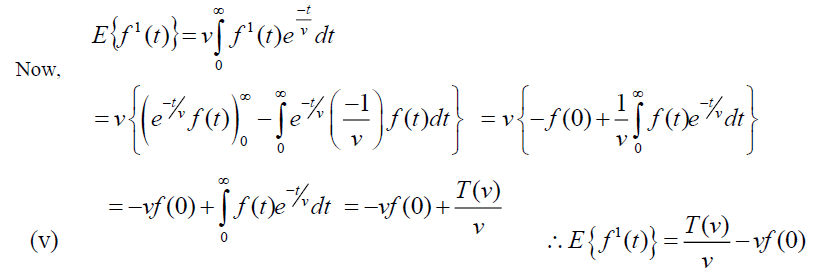
Theorem: Let f (t) be the given function and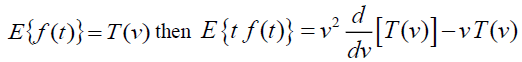 
Proof: Given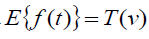 
, By Definition of Elzaki Transform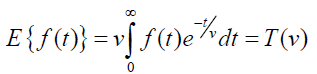
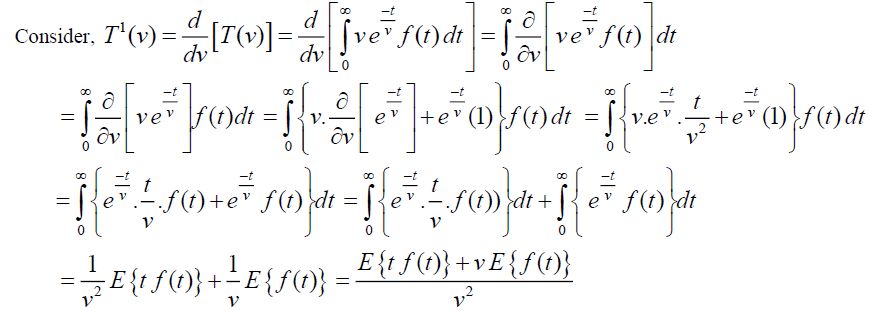
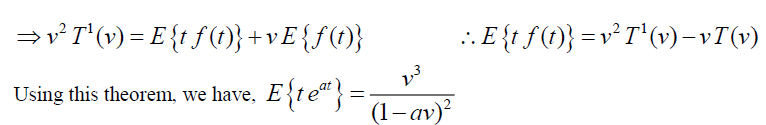
Discussion
Application and analysis
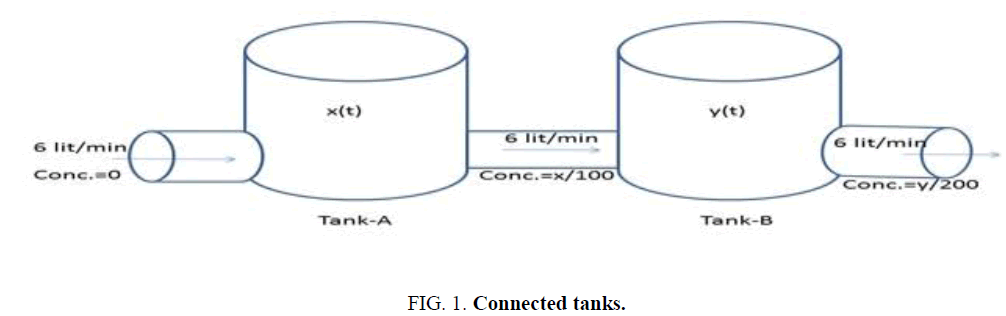
Example 1: Suppose, we connected two tanks by pipes. First tank contains 100 liters of water and 40 grams of salt. And the second tank contains 200 liters of water and 60 grams of salt and if fresh water enters into first tank at 6 liters per minute and first tank drains into second tank at 6 liters per minute and of solution is pumped at the same rate from the second tank to the first. Find the salt content in each tank as a function of time.
Solution: Let us assume that the two tanks are tank-A and tank-B (Figure 1).
Figure 1: Connected tanks.
And let x (t) be the amount of salt at any time in the tank-A and y (t) be the amount of salt at any time in the tank-B.
For Tank A we have,
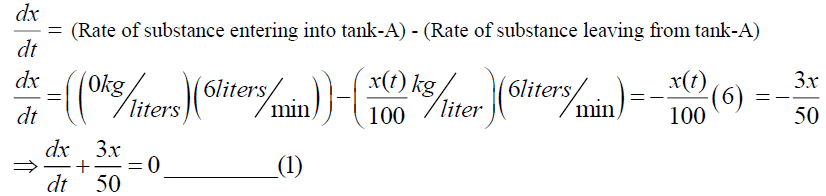
At the initial time t=0, x (0)=40. Similarly, for tank-B we have,
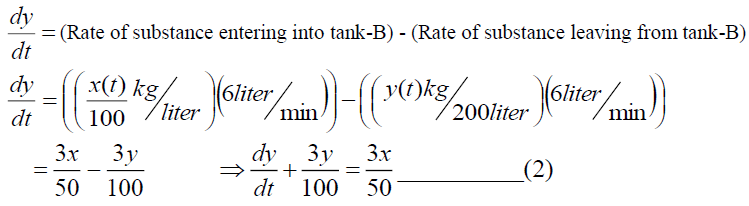
At the initial time t=0, y (0)=60. Taking Elzaki Transform of Equation (1)
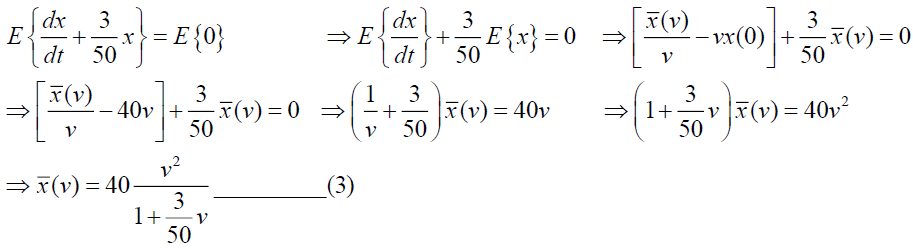
Taking Inverse Elzaki Transform of equation of (3) we get,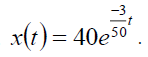 
Taking Elzaki Transform of equation (2) we have,
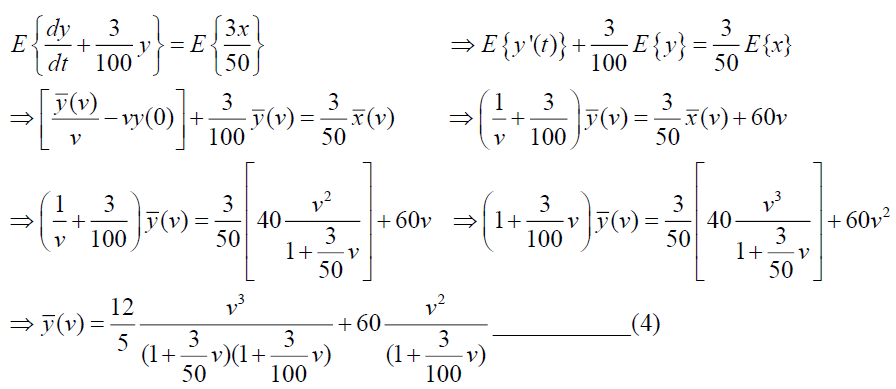
For simplification we consider,
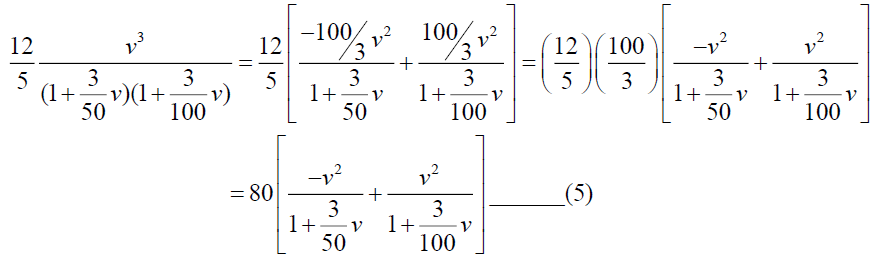
Now Substituting (5) in (4), we get
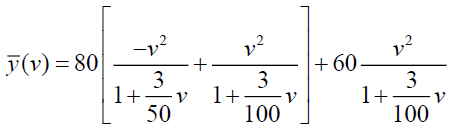
Taking Inverse Elzaki Transform on both side of above equation, we get
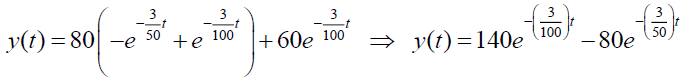
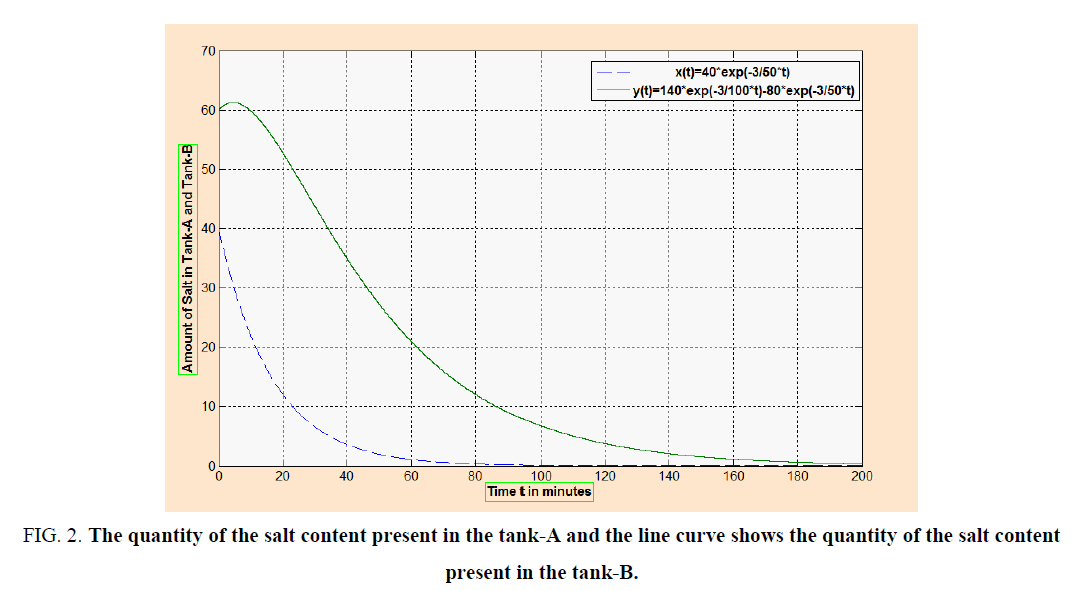
The schematic diagram of this problem is shown below in Figure 2. The dotted curve in the graph shows the quantity of the salt content present in the tank-A and the line curve shows the quantity of the salt content present in the tank-B at any point of time.
Figure 2: The quantity of the salt content present in the tank-A and the line curve shows the quantity of the salt content present in the tank-B.
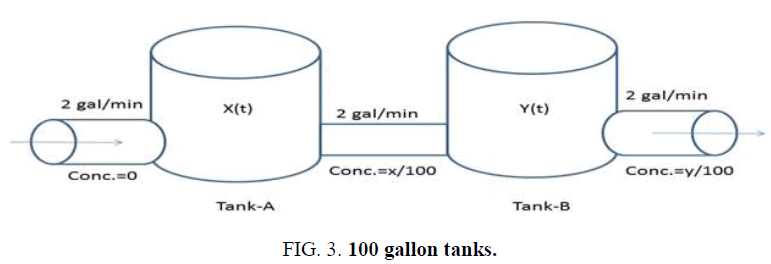
Example 2: We have two 100 gallon tanks. Tank-A is initially full of salt water with a salt concentration 0.5 liter/gallon. Tank-B is full of pure water. Pure water enters tank-A at 2 gal/min water exists the well mixed tank A at two gal/min and flows into tank-B. Water also exist tank-B at two gal/min and flows out of the system. Find the amount of salt in both tanks [3-5].
Solution: Let us assume that the amount of water in the pipe between the tanks is negligible. Let x (t) be the amount of salt in pounds in tank-A at time t and y (t) be the amount of salt in pounds in tank-B at time t. Thus, the concentration in tank A and tank B are x/100 and y/100 respectively (Figure 3).
Figure 3: 100 gallon tanks.
The differential equation describing the rate of change of the amount of salt in tank-A is,
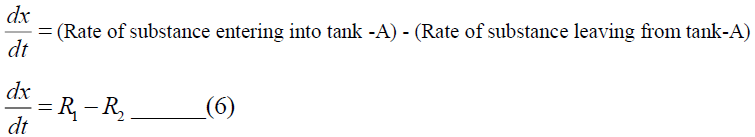
Where,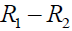 
=Rate of substance entering into tank A - Rate of substance leaving tank-A
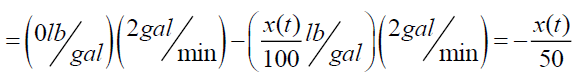
From (6),
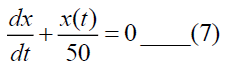
Initially, the concentration of salt in tank-A=(0.5) (100)=50. i.e. at t=0, x(0)=50.
For tank-B, we have 
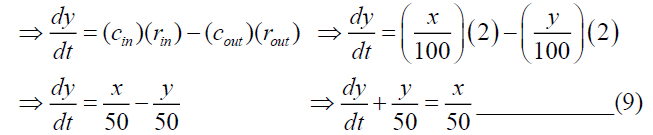
From the equation (7), we have
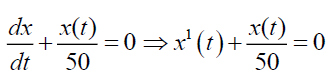
Taking Elzaki transform on both sides we have,
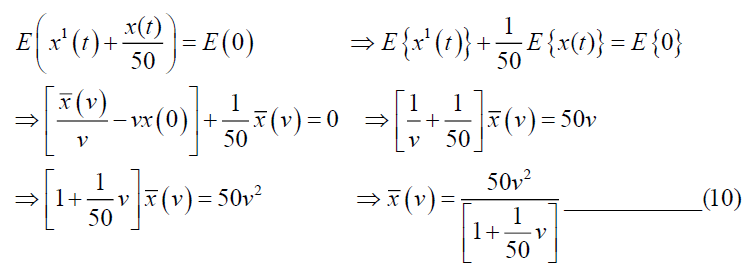
Taking inverse Elzaki transform of equation (10), we have
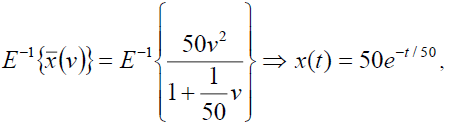
From the equation (9), we have
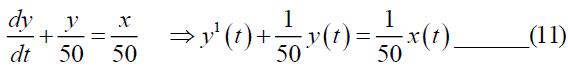
Taking Elzaki transform on both sides of (11) we have,
Taking inverse Elzaki transform of equation (12), we get,
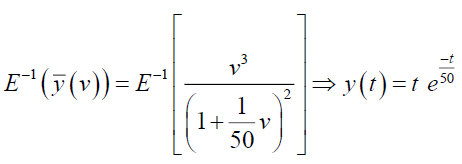
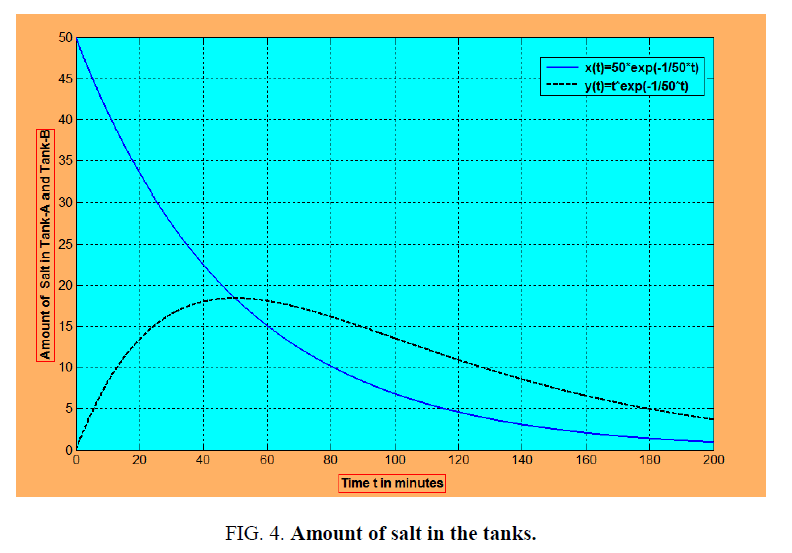
From the schematic diagram given in the below in Figure 4 shows that the amount of salt in the tank-A exponentially decays, but in the tank-B it is increases due to the inflow of salt from the tank-A and then the amount of salt in the tank-B decreases.
Figure 4: Amount of salt in the tanks.
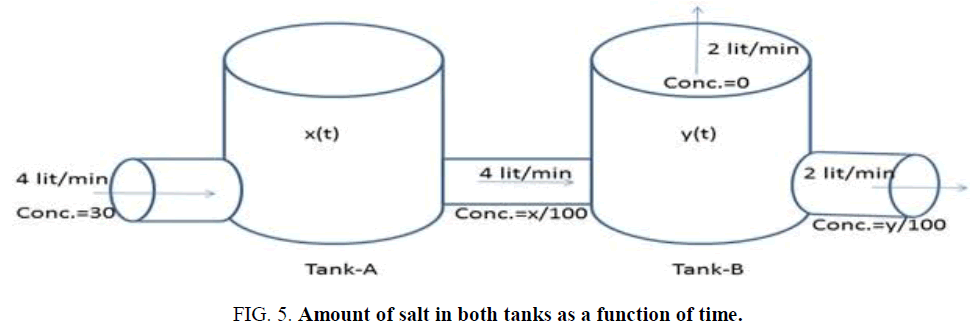
Example-3: Two well mixed 100 liter tanks are initially full of pure water. Water containing salt at a concentration of 30 g/liter flows into tank-A at a rate of 4 liters/min. Water flows from tank-A to tank-B at 4 liters/min. water evaporates from tank-B at 2 liters/min and flows out at 2 liters/min. Find the amount salt in both tanks as a function of time.
Solution: Assume that, x (t) and y (t) are the amount of salt in tank-A and tank-B respectively at time t measured in minutes, and x, y is in grams (Figure 5).
Figure 5: Amount of salt in both tanks as a function of time.
The equation describing the change in the amount of salt is,
In tank-A:
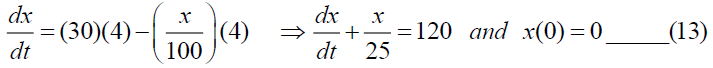
In tank-B;
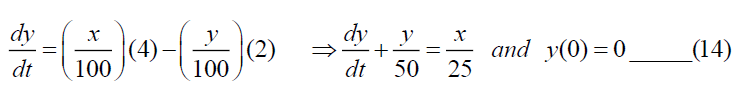
Taking Elzaki Transform of (13),
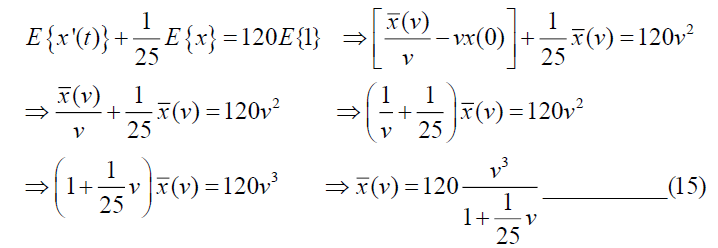
Taking Inverse Elzaki Transform of (15), we get,
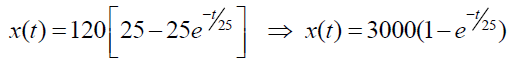
From (14) we have,
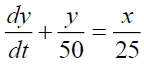
Taking Elzaki Transform on both sides of above equation, we get
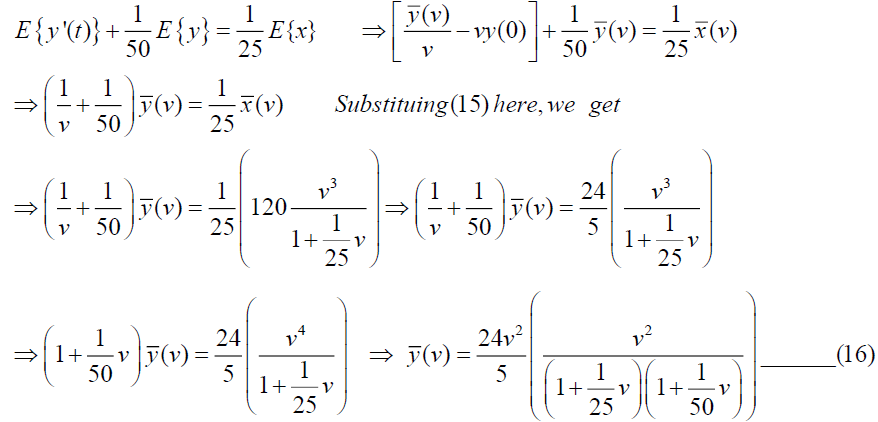
We can write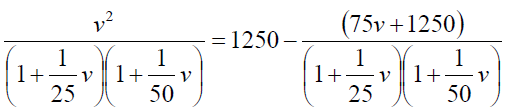 
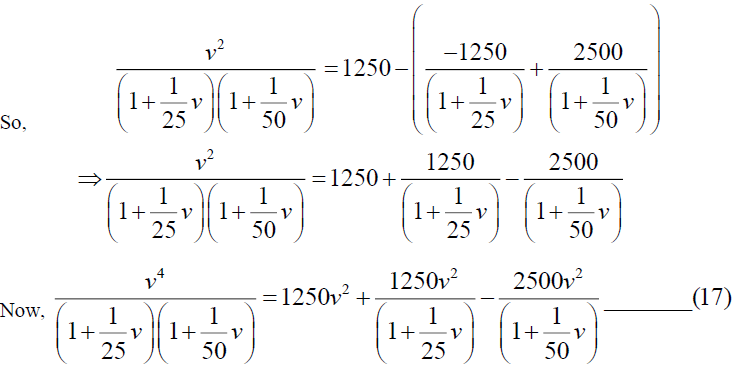
From equation (16) and (17), we get,
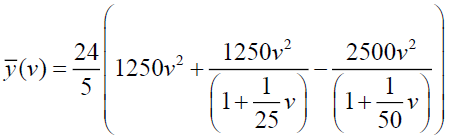
Now by taking inverse Elzaki transform we get,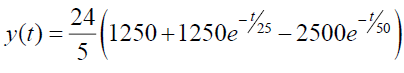 
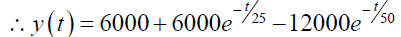
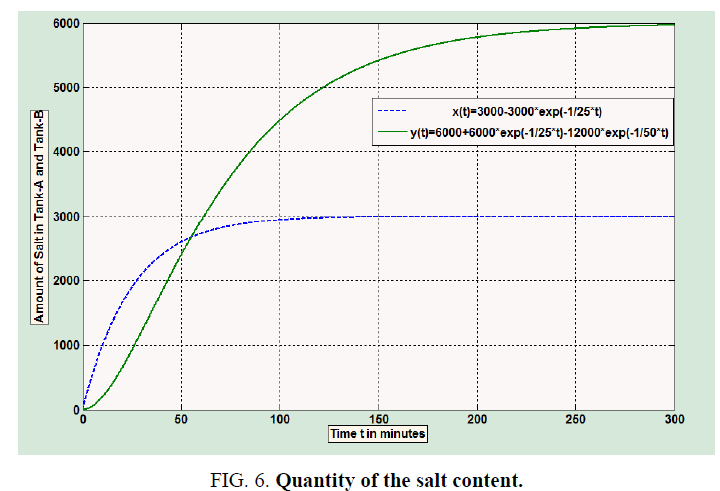
In the graph bellow (Figure 6) the dotted curve in the graph shows the quantity of the salt content present in the tank-A and the line curve shows the quantity of the salt content present in the tank-B at any point of time.
Figure 6: Quantity of the salt content.
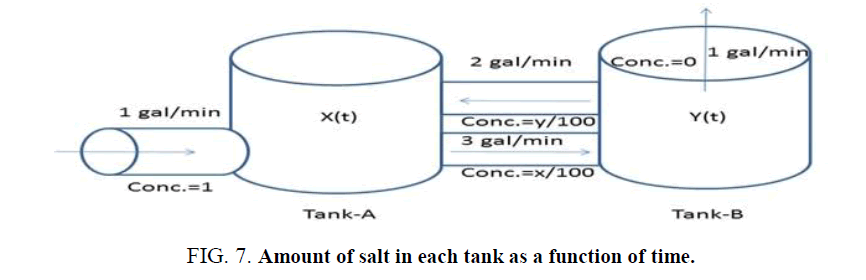
Example 4: There are two 100 gallon tanks both initially full of pure water. Water containing salt at a concentration of 1 ltr/gal flows into tank-A from an outside source at 1gal/min. Water flows from tank-A to Tank-B at 3 gal/min. Water evaporates from tank-B at 1 gal/min and is piped back to tank-A at 2 gal/min. Find the amount of salt in each tank as a function of time.
Solution: Let x (t) and y (t) are the amount of salt in tank-A and tank-B respectively at any time (Figure 7).
Figure 7: Amount of salt in each tank as a function of time.
The differential equation for tank-A,
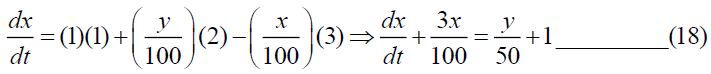
At time t=0, x (0)=0. Similarly, for tank- B, we get,
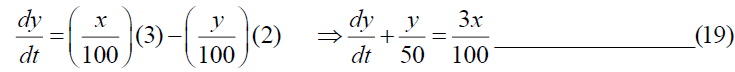
At time t=0, y (0)=0. Taking Elzaki Transform on (18), we get
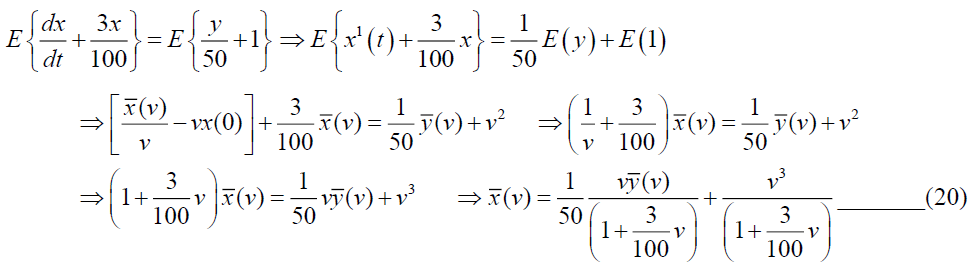
Taking Elzaki Transform on (19),
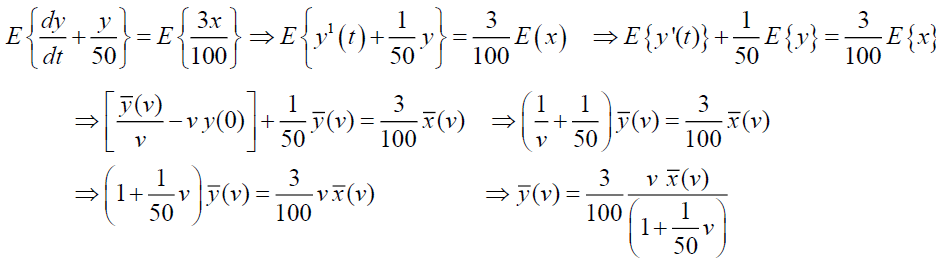
Substituting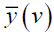 
in the equation (20), we have,
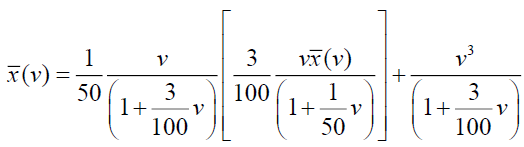
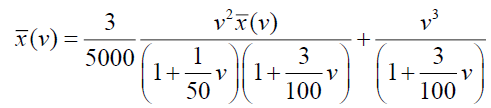
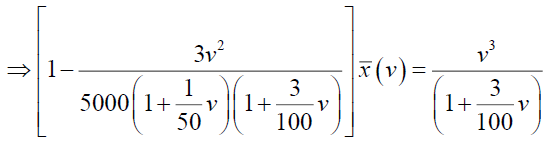
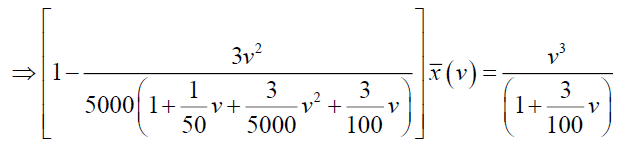
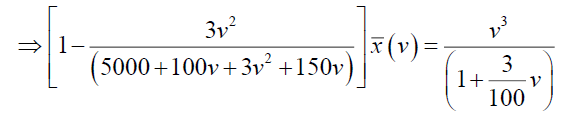
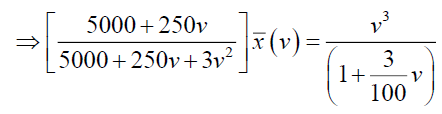
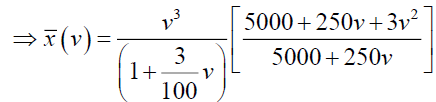
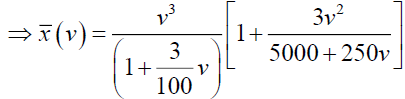
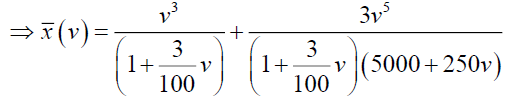
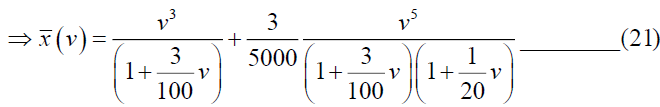
Now consider,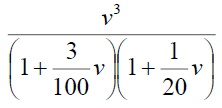 
and which can be written as,
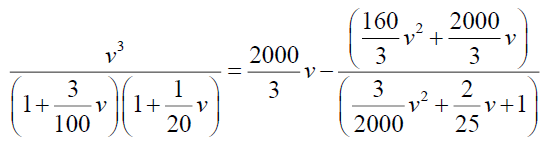
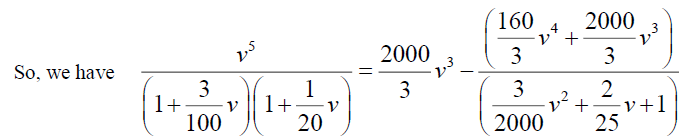
Now
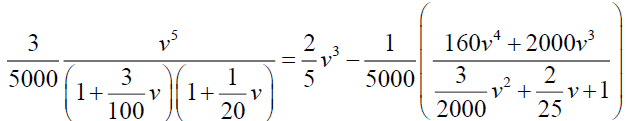
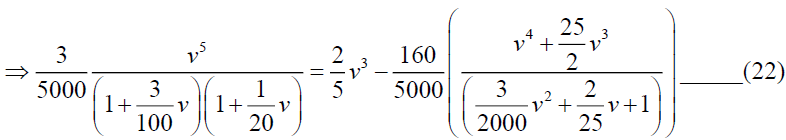
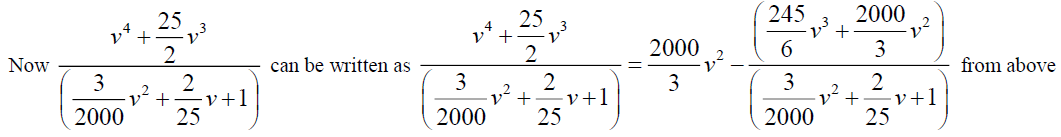
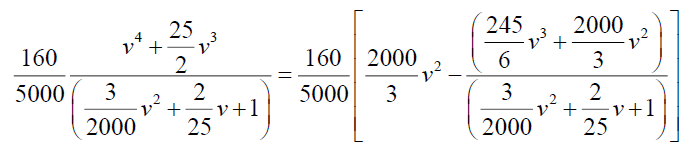
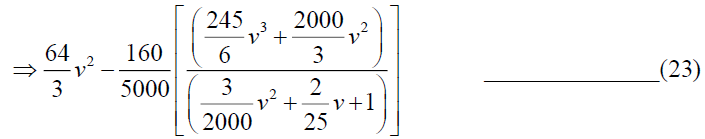
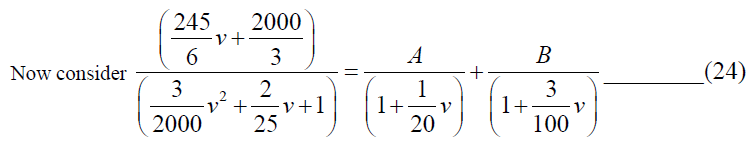
By simplifying we have A=-375 and B=3125/3, so from (24)
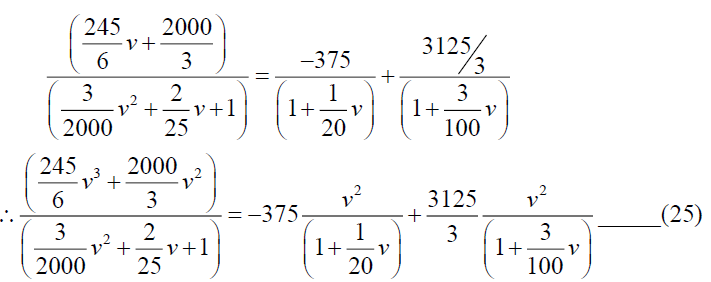
From equations (23) and (25), we get,
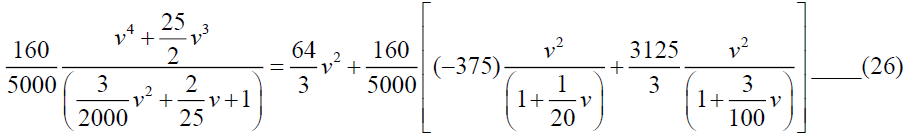
From equations (22) and (26), we get,
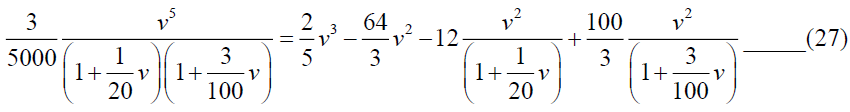
From equations (21) and (27), we get,
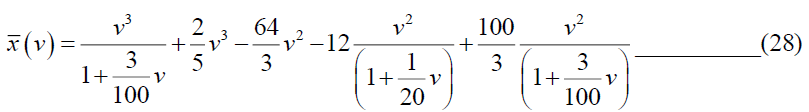
Taking inverse Elzaki transform of equation (28), we get,
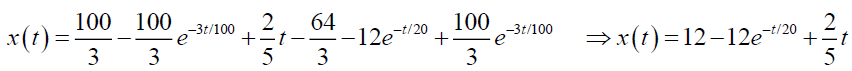
From the equation (18), we get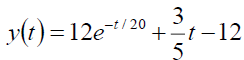 
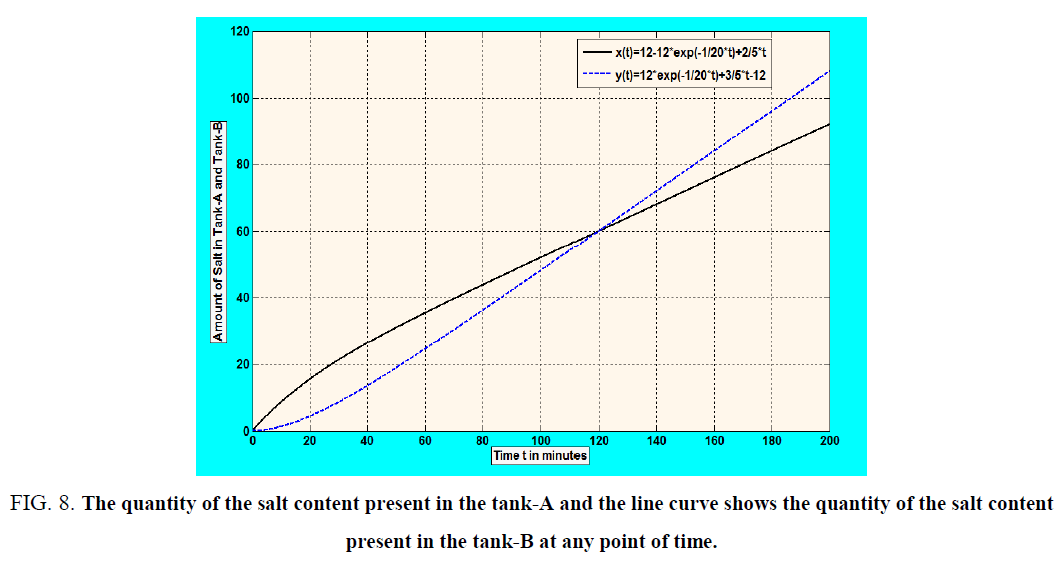
The schematic diagram for this problem is shown below in Figure 8, in which the dotted curve shows the quantity of the salt content present in the tank-A and the line curve shows the quantity of the salt content present in the tank-B at any point of time.
Figure 8: The quantity of the salt content present in the tank-A and the line curve shows the quantity of the salt content present in the tank-B at any point of time.
Conclusion
Elzaki Transform is one of the suitable methods to solve the problems related to two tank problems in which data is presented in the form of system of linear differential equations.
References
- Elzaki TM. The New Integral Transform “Elzaki Transform”. Glob J Pure App Math. 2011;7(1):57-64.
- Jeffrey A. Analysis of fractional differential equations. Advanced Engineering Mathematics, Academic Press. 2002.
- Eltayeh H, Kilicman A. On some application of a new integral transform. Int J Math Analysis. 2010;4(3):123-32.
- Zhang J, Sumudu A. Based algorithm for solving differential equations. Comp Sci J. 2007;15(3):303-13.
- Kwatugala G. Sumudu transform: An integral transform to solve differential equations control engineering problems. Int J Math Ed Sci Tech. 1993;24:35-43.
