Original Article
, Volume: 6( 3)Double Hopf Bifurcation of a Simply Supported Rectangular Thin Plate With Parametrically and Externally Excitations
- *Correspondence:
- Zhou Y, Mathematics Science College, Inner Mongolia Normal University, Hohhot 010022, China, Tel: +864714392030; E-mail: yanzhou0924@163.com
Received: August 22, 2017; Accepted: September 05, 2017; Published: September 8, 2017
Citation: Zhou Y. Double Hopf Bifurcation of a Simply Supported Rectangular Thin Plate with Parametrically and Externally Excitations. J Space Explor. 2017;6(3):128
Abstract
Based on the singularity theory, the double Hopf bifurcation problem of a rectangular thin plate with four edges simply supported under the combined actions of the parametric excitation and the external excitation are investigated in the case of the principal parametric resonance and internal resonance. Considering weak damping and weak excitation, the bifurcation equation of the thin plate system is obtained, and the bifurcation diagrams of the thin plate system are given on the parameter plane. Then, the stationary solutions and its stability for the rectangular thin plate are analyzed.
Keywords
Double Hopf bifurcation; Classification and unfolding; Thin plate; Periodic solution
Introduction
In recent years, many scholars began to pay attention to the double Hopf bifurcations of some nonlinear dynamic system. The resonant double Hopf bifurcation will lead to complex dynamic phenomena in nonlinear dynamical systems, such as torus and periodic orbits, period doubling, homoclinic and heteroclinic connections and chaos.
Nayfeh and Mook [1] studied the high dimensional dynamical system with several pairs of pure imaginary roots. The local dynamic behavior of double Hopf bifurcation was analyzed by using the method of frequency domain with Mess and Chua [2]. With the aid of Poincare maps Xie and Ding [3] investigated a three degree of freedom vibrio impact system with double Hopf bifurcation and invariant tori, in which the rich bifurcation phenomena are found. Yu [4] considered the non-resonant double Hopf bifurcation of a class of dynamical system by using computer algebra, and the canonical form of nonlinear dynamic system was calculated by the method of multiple scales, and the calculation program of double Hopf bifurcation was given.
The double Hopf bifurcation of a class of delay differential dynamical system was studied by using the normal form theory, and the stability of the equilibrium points of the linear system were analyzed by Orosz and Stépán [5]. Revel et al. [6] considered the double Hopf bifurcation problem of a class of coupled circuit system, and the parameter bifurcation diagram was obtained. Zhang and Xu [7] used the Hopf bifurcation theorem to study the non-resonant double Hopf bifurcation of Van der Pol-duffing system with time delay.
Buono and Belair [8] analyzed the non-resonant double Hopf bifurcation point of the scalar delay differential system by using the Normal form theory. Bel and Reartes [9] studied the Hopf bifurcation, double Hopf bifurcation and the Neimark Sacker bifurcation of van der Pol-duffing system. Using the canonical form method and the center manifold theorem, Li et al. [10] researched the almost periodic attractors and the double Hopf bifurcation response of a time delay coupled system. The bifurcation diagram of the system was given by numerical simulation. For high dimensional nonlinear systems, due to the limitation of the methods, the research on the system for the resonant double Hopf bifurcation is not perfect.
The 1: 2resonance double Hopf bifurcation phenomena of several kinds of dynamical systems were studied by Campbell and LeBlanc [11]. Luongo et al. [12] considered the 1: 2 and 1:3 resonance double Hopf bifurcations by using the method of multiple scales. Subsequently, Xu and Chung [13] researched 1: 2 Hopf bifurcation phenomena of a class of Van der Pol dynamical system with time delays, and illustrated that there exist the codimension-2 or codimension-3 bifurcation behavior. The k : l resonant double Hopf bifurcation behavior of differential equations was studied by Broer et al. [14]. Revel et al. [15] studied the 2:3resonant double Hopf bifurcation of a four-dimensional autonomous system, in which, the global bifurcation behavior of the system was analyzed. Saleh and Wagener [16] analyzed the 1: 2 and 1:3 resonant double Hopf bifurcation by using the singularity theory and normal form theory and gave the stability analysis of the periodic solution and almost periodic solution for the system. Wang and Xu [17] considered the 1:3 resonance double Hopf bifurcation of a time delay system.
Thin plates were widely used in aerospace and other engineering fields. In recent years, much progress has been made on nonlinear vibration and bifurcation problems on the dynamics of thin plates. Hadian and Nayfeh [18] used the method of multiple scales to study the nonlinear responses of the clamped circular plate under harmonic excitation with internal resonance. Yang and Sethna [19] investigated the local bifurcation and global bifurcation of the square thin plate with parametric excitation by using the average method and shown the system can take the chaotic motion in the sense of the Smale Horseshoe.
The global bifurcation and chaotic dynamics of a rectangular thin plate with four edges simply supported under the combined actions of parametric excitation and external excitation were studied by Zhang et al. [20,21]. Awrejcewicz and Krysko [22] analyzed the periodic, almost periodic and chaotic motions of a thin plate under longitudinal and time varying loads. Awrejcewicz and Krysko [23] used Bubnov-Galerkin method to study the nonlinear dynamic responses of the flexible thin plate system. With the aid of energy phase method, Yao and Zhang [24] studied the multi-pulse chaotic dynamics of a thin plate under the combined actions of the parametric excitation and external excitation. Zhang et al. [25] considered the multipulse chaotic dynamic responses of a Shilnikov type of non-autonomous buckling thin plate under parametric excitation using high dimensional Mlenikov method. The nonlinear vibration responses of a simple supported circular plate were studied by Akour and Nayfeh [26]. Zhou and Zhang [27] investigated the double Hopf bifurcation of a piezoelectric composite laminates with the combined external excitation and internal excitation by using the method of multiple scales and singularity theory, then, the bifurcation diagram and the different steady state solutions of the average equations were analyzed for the nonlinear system.
This paper aims at studying the double Hopf bifurcation of a rectangular thin plate with four edges simply supported under the combined actions of parametric excitation and external excitation. We first using the method of multiple scales transform a two degree of freedom nonlinear system into autonomous equation. Two different coordinates of averaged equation of the thin plate are analyzed. The existences of periodic and almost periodic motions of the nonlinear system in a certain condition are given by the numerical simulation, and the classification of bifurcation solutions of the nonlinear system are analyzed in different regions of the parameter space.
Experimental
Double Hopf bifurcation of rectangular thin plate with primary parameter resonance, i.e., 1:3 internal resonance
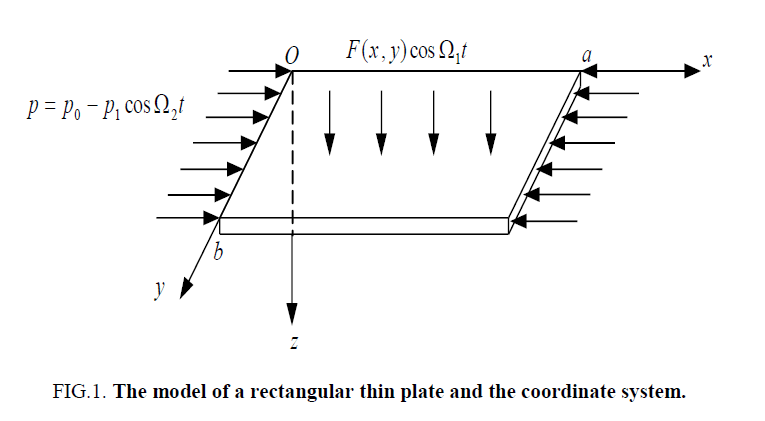
We consider a rectangular thin plate under simply supported on four edges, its length is a and b , and the thickness is h . The thin plate subjected to transverse excitation and internal excitations. A Cartesian coordinate system is shown in Figure 1.
Figure 1: The model of a rectangular thin plate and the coordinate system.
The coordinate Oxy is located on the middle surface of the thin plate, u ?v and w are the displacements of a point on the surface of the thin plate of the x ?y and z direction, respectively.
According to Chia [28], using the Hamiltons principle and Reddy order shear deformation theory, we got the two degree of freedom nonlinear dynamic equation which can be written as follows,
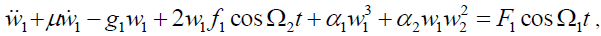 (1a)
(1a)
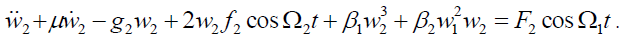 (1b)
(1b)
Assuming the nonlinear system (1) is weakly nonlinear system, adding a small perturbation ε to the damping terms, parametric excitation terms, external excitation terms and nonlinear terms, we obtain the following equations,
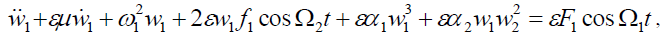 (2a)
(2a)
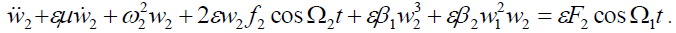 (2b)
(2b)
Consider the primary parametric resonance, i.e., internal resonance of the thin plate; we have the following resonance relationship:
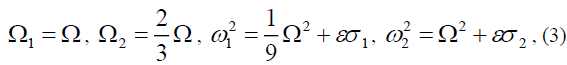
Where, σ1 and σ2 are two detuning parameters.
For convenience of analysis, let Ω=3. Using the method of multiple scales [1], we obtain the average equation of the thin plate in the plural form,
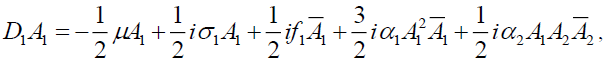 (4a)
(4a)
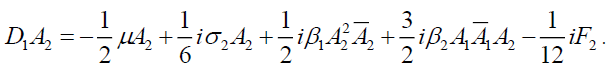 (4b)
(4b)
The average equation in the Cartesian form will be expressed as,
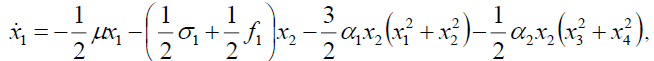 (5a)
(5a)
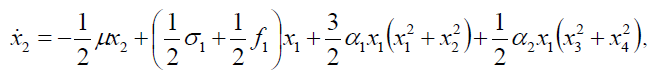 (5b)
(5b)
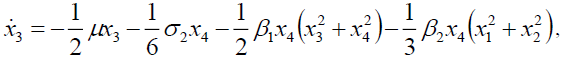 (5c)
(5c)
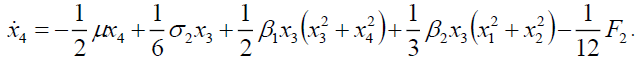 (5d)
(5d)
Let
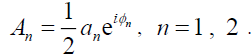 (6)
(6)
Put the equation (6) into equation (4), the average equation of the thin plate in the Polar form is obtained as follows:
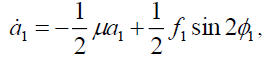 (7a)
(7a)
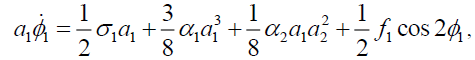 (7b)
(7b)
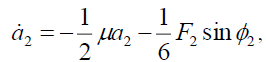 (7c)
(7c)
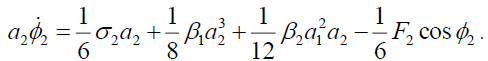 (7d)
(7d)
In order to study the steady state solutions of equation (7), namely the periodic solutions or quasi-periodic solutions of equation (2), let the left side of the equation (7) equal to zero. Then, the bifurcation response equation of the thin plate can be written as follows,
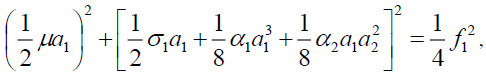 (8a)
(8a)
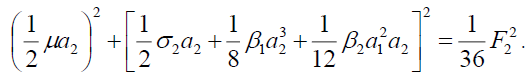 (8b)
(8b)
Next, we will consider the various stationary solutions of equation (8) and its changing situation with the variable parameters 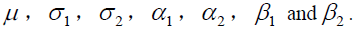 In order to facilitate the analysis, take
In order to facilitate the analysis, take 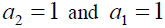 in equations (8a) and (8b), respectively, then the equation (8) can be expressed as:
in equations (8a) and (8b), respectively, then the equation (8) can be expressed as:
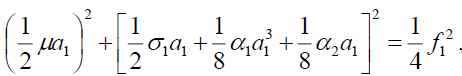 (9a)
(9a)
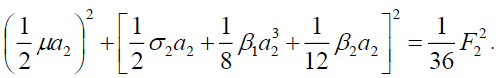 (9b)
(9b)
After simplification, the bifurcation response equation of the thin plate is obtained as follows:
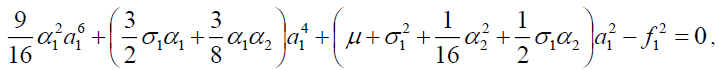 (10a)
(10a)
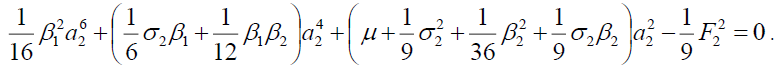 (10b)
(10b)
Let,
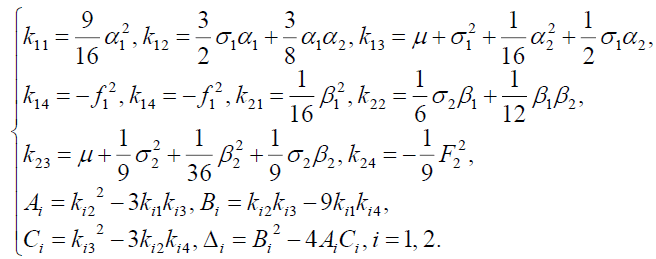 (11)
(11)
Take the equation (11) into equation (10), we get the following several different stationary solutions for the bifurcation equation (10). The specific circumstances are as follows.
(1) Since the following condition is satisfied, namely,
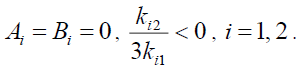 (12)
(12)
Three solutions will exist for equation (10), which can be written as:
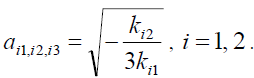 (13)
(13)
(2) When 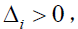 namely,
namely,
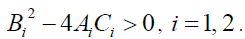 (14)
(14)
And
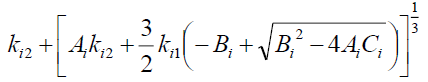
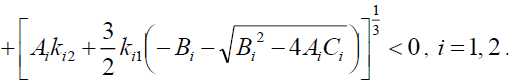 (15)
(15)
then, there are two solutions for equation (10),
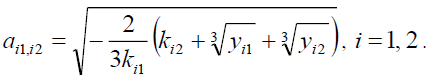 (16)
(16)
Where
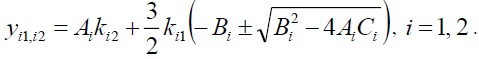 (17)
(17)
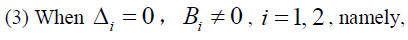
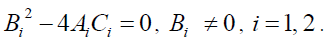 (18)
(18)
If the following condition is also satisfied,
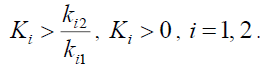 (19)
(19)
The equation (10) will have one solution, namely,
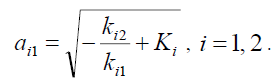 (20)
(20)
If there
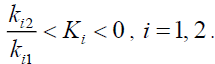 (21)
(21)
There are three solutions for equation (10), which can be written as:
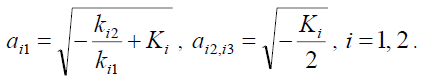 (22)
(22)
If there
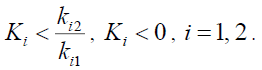 (23)
(23)
then, there will have the following two solutions for equation (10),
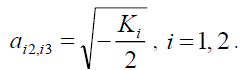 (24)
(24)
(4) At last, when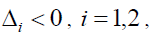 namely,
namely,
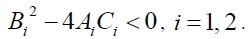 (25)
(25)
There will be three situations about the solutions for equation (10), namely,
If there
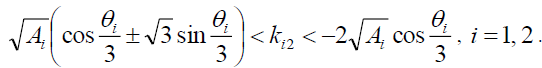 (26)
(26)
the equation (10) will have one solution
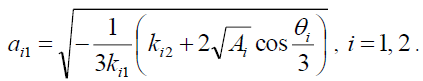 (27)
(27)
If there
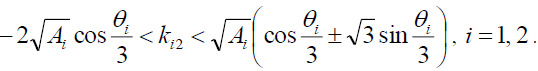 (28)
(28)
The equation (10) will have two solutions:
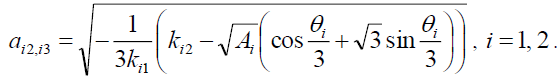 (29)
(29)
If there,
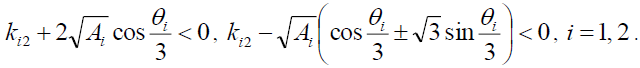 (30)
(30)
The equation (10) then will have three solutions
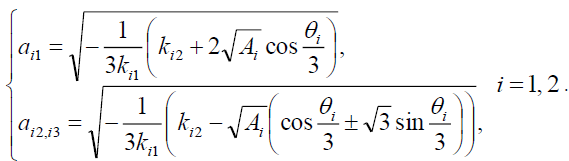 (31)
(31)
Where
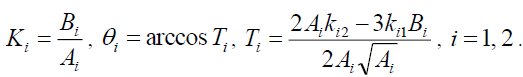 (32)
(32)
In order to determine the stability of the solutions for equation (7), we should consider the Jacobi matrix of equation (5). The Jacobi matrix of equation (5) at the zero-solution point is written as:
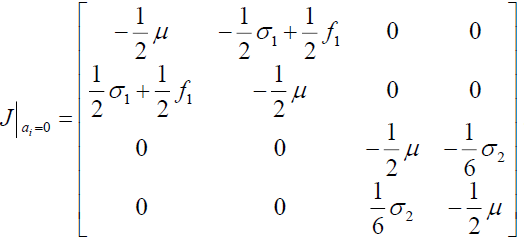 (33)
(33)
The corresponding characteristic equation is
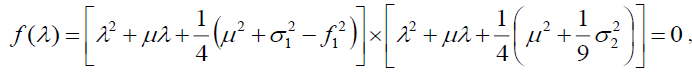 (34)
(34)
And the Eigen values are,
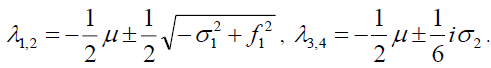 (35)
(35)
The Jacobi matrix of equation (2) on the non-zero solution point can be written as:
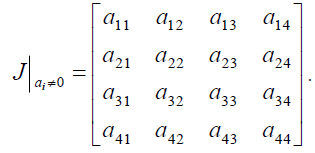 (36)
(36)
The corresponding characteristic equation is,
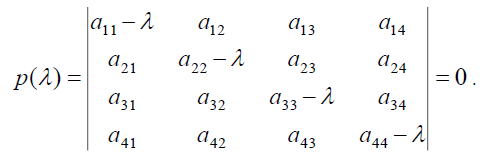 (37)
(37)
In order to conveniently express, the characteristic equation (37) can be expressed as:
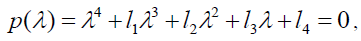 (38)
(38)
And the Eigen values of equation (5) are,
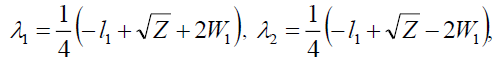
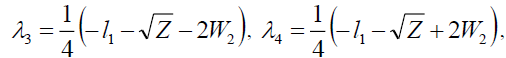 (39)
(39)
All the coefficients in equations (38) and (39) are shown in Appendix.
Based on the aforementioned analysis, the stability conditions for the non-zero solutions are:
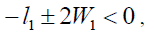 (40).
(40).
 (41)
(41)
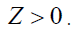 (42)
(42)
It is found from the aforementioned analysis that the solutions given in equations (13), (16), (20) and (27) can meet the conditions in the equation (42), while the solutions given by equations (24) and (29) do not satisfy the conditions in the equation (42).
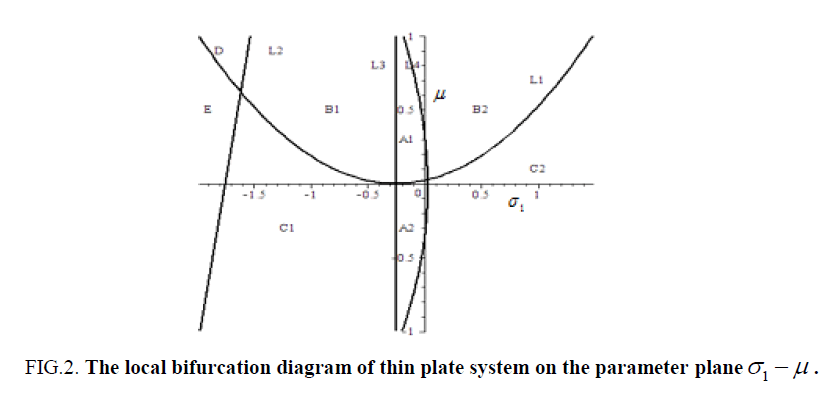
Based on the theory of bifurcation, the parameter plane 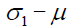 is divided into several different regions by the stability critical curves for the steady solutions. These critical curves give the local bifurcation set for the nonlinear system (2), as shown in Figure 2.
is divided into several different regions by the stability critical curves for the steady solutions. These critical curves give the local bifurcation set for the nonlinear system (2), as shown in Figure 2.
Numerical simulations
In this section, we use MAPLE to study the nonlinear vibration response of the simply supported rectangular thin plate under the combined effects of transverse excitation and in-plane excitation with the primary parametric resonance and 1:3 internal resonance.
According to the aforementioned analysis, we choose that the parameters and the initial values of equation (2) are
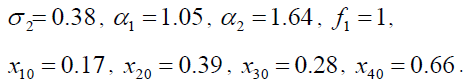
The local bifurcation diagram is depicted for the rectangular thin plate with four edges simply supported in the parameter plane 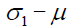 as shown in Figure 2.
as shown in Figure 2.
(1) In the areas A1 and A2, the zero solution is the unique singular point. From the equation (36), we know that the singular point is steady focus in the region A1, so that, the zero solution is stable, and the singular point is unsteady focus in the region A2, therefore, the zero solution is unstable in this situation.
(2) When crossing the line L3, the zero solution change its stability, a pair of complex conjugate eigenvalues of equation (2) crossing the imaginary axis and become to a pair of simple pure imaginary eigenvalues, the system (1) occurs Hopf bifurcation, and limit cycles will occur from the initial point. When crossing the line L2 and L4 , the stability of zero solution will also change, two pairs of complex conjugate eigenvalues will cross the imaginary axis and become to two simple pure imaginary eigenvalues, the system will take double Hopf bifurcation.
(3) In the areas B1, B2 and E, the number of steady solutions unchanged, and the steady solutions are stable.
(4) When crossing the curve L1 from area B1 into area C1, on the arc L1, one eigenvalue of equation (2) becomes to zero, then the stability of the singularity points for the nonlinear system sensitively depend on the varying parameters in equation (10). In the region C1, the singular point is a saddle point, so the zero solution is unstable, and the system will produce Pitchfork bifurcation, that is, two non-zero solutions will bifurcate from the zero solution, as shown in equation (16).
(5) When crossing the curve L1 from area B2 into area C2, on the curve L1, one eigenvalue becomes to zero, the other two non-zero solutions bifurcate from the zero solution, as shown in equation (29), and the nonlinear system (1) produces Pitchfork bifurcation. It is easily known that the two non-zero solutions are unstable.
(6) In the region D, the solution for equation (27) is a saddle point, so this solution is unstable.
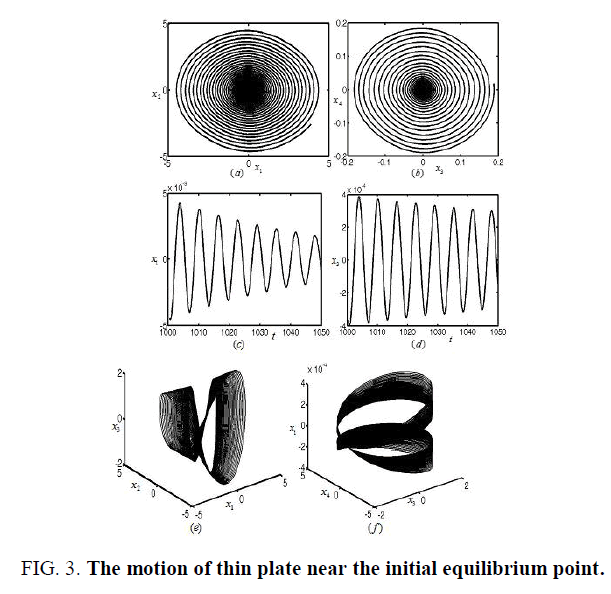
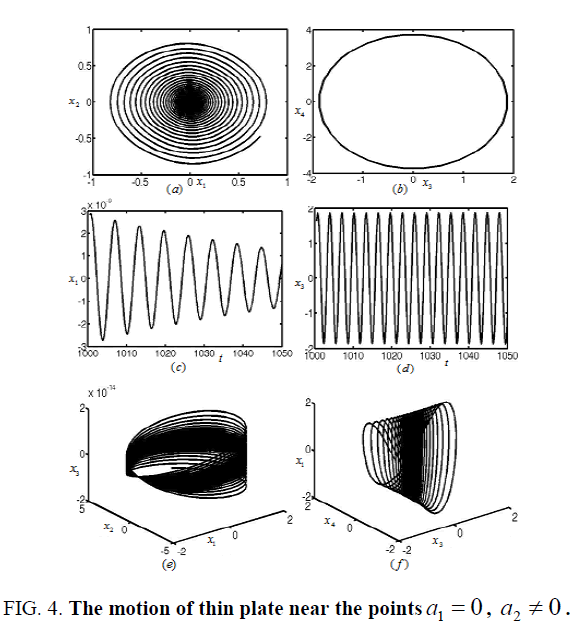
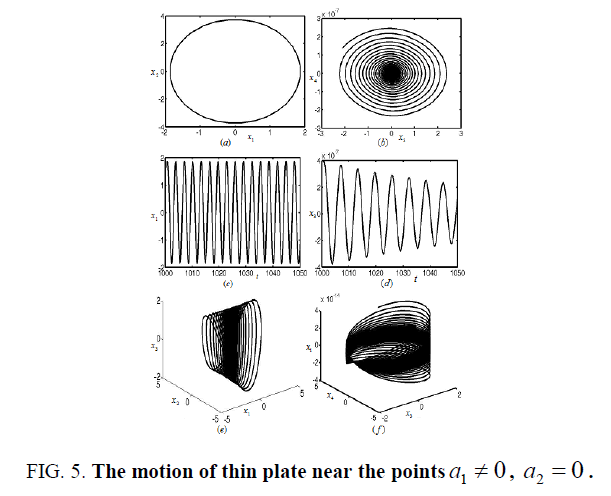
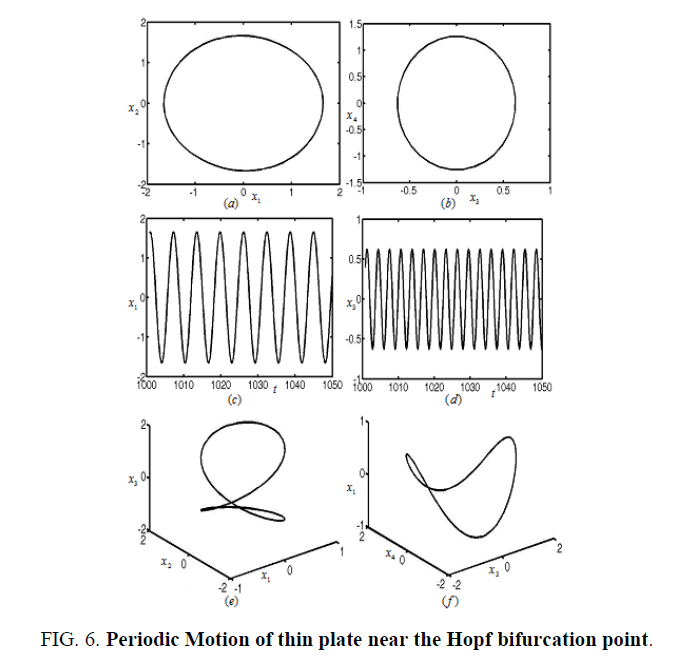
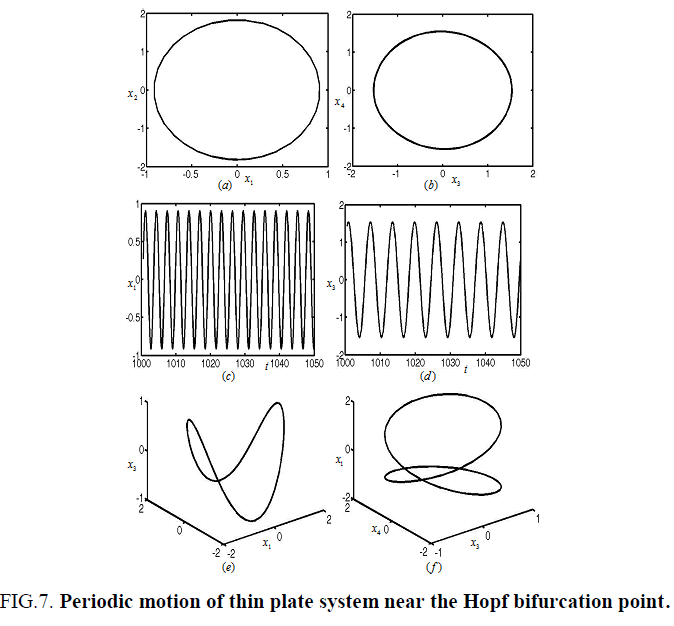
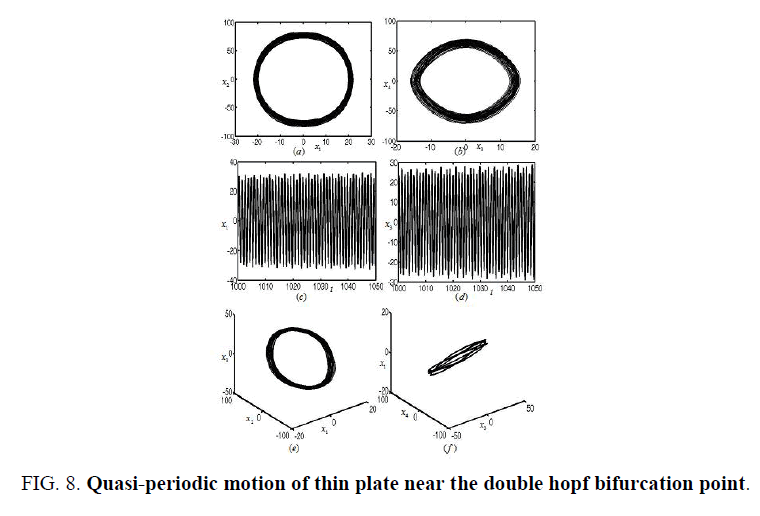
Figures 3-8 represent the different forms of nonlinear vibration characteristics of the rectangular thin plate, respectively. In the following figures, diagrams (a) and (b) represent the two-dimensional phase diagrams on the plane 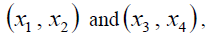 respectively. Graphs (c) and (d) are the waveform diagrams on the planes
respectively. Graphs (c) and (d) are the waveform diagrams on the planes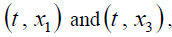 respectively. Diagrams (e) and (f) are the three-dimensional phase diagrams in the spaces
respectively. Diagrams (e) and (f) are the three-dimensional phase diagrams in the spaces 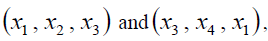 respectively.
respectively.
Select the damping coefficient and tuning parameters of the piezoelectric composite laminates are μ = 0.21 and σ1= 0.17 as in area A1 in Figure 2. We obtain the nonlinear vibration near the equilibrium solutions of the rectangular thin plate, as shown in Figure 3. From the phase Figure 3(a) and Figure 3(b), we know that the solutions of the system tend to zero solution. Then, it is asymptotically stable.
To continue changing the damping coefficient and tuning parameters of the rectangular thin plate to μ = 0.09 and σ1= -0.18 as in area A2 in Figure 2. The nonlinear vibration of the rectangular thin plate is shown in Figure 4 near the stationary solution 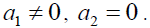
When the damping coefficient and tuning parameters of composite laminated piezoelectric plate are μ = 0.30 and σ1= -0.68, and μ = 0.30, σ1= -1.92 as in area B1 and E in Figure 2, respectively. The equilibrium solution of the rectangular thin plate will generate Hopf bifurcation. The nonlinear vibration of the rectangular thin plate is periodic motion, as shown in Figure 6 and Figure 7.
Let μ = 0.67 and σ1= 0.4 as in area B2 in Figure 2, we obtain the 1:3 resonant double Hopf bifurcation. Subsequently, the nonlinear response of the rectangular thin plate is almost periodic vibration, as shown in Figure 8.
Results, Discussion and Conclusion
Based on the singular theory for high dimensional nonlinear system, the double Hopf bifurcations of the rectangular thin plate are studied in the primary parametric resonance, i.e., 1:3 internal resonance.
Using the method of multiple scales, the averaged equation of the rectangular thin plate is obtained. Furthermore, the bifurcation equation of the rectangular thin plate is achieved. Through the analysis of the bifurcation equation of the system, the nonlinear dynamic responses of the rectangular thin plate are analyzed on the parameter plane based on the bifurcation diagram as shown in Figure 2. Selecting the damping coefficient, external excitation, excitation parameters and detuning parameters as different values, the nonlinear vibration forms of the rectangular thin plate are analyzed under the combined actions of parametric and external excitation using the numerical approach, as shown in Figures 3-8. The theoretical and numerical results indicated that Hopf bifurcation and double Hopf bifurcations occur for the rectangular thin plate.
Further research jobs will be done based on this paper, such as, the detail analysis of local and global bifurcations of the piezoelectric composite laminated plate, and the investigation of the classification and unfolding of the piezoelectric composite laminated plate.
Acknowledgements
The authors gratefully acknowledge the support of National Natural Science Foundation of China (NNSFC) through grant Nos. 11402127, 11290152 and 11402126, the Funding Project for Academic Human Resources Development in Institutions of Higher Learning under the Jurisdiction of Beijing (PHRIHLB).
References
- Nayfeh AH, Mook DT. . Wiley, New York; 1979.
- Mess AI, Chua LO.The Hopf bifurcation theorem and its applications to nonlinear oscillations in circuits and system . IEEE T Circuits. 1979;26:235-54.
- Xie JH, Ding WC. of a vibro-impact system . Int J Nonlin Mech. 2005;40:531-43.
- Yu P.Analysis on double Hopf bifurcation using computer algebra with the aid of multiple scales . . 2001;27:19-53.
- Orosz G, Stépán G.Subcritical Hopf bifurcations in a car-following model with reaction time delay . . 2006;462:2643-70.
- Revel G, Alonso DM, Moiola JL. . Int J Bifurcat Chaos. 2008;18:481-94.
- Zhang Y, Xu J. . Int J Nonlin Sci Num. 2005;6:63-68.
- Buono PL, Belair J. . J Differ Equat. 2003;189:234-66.
- Bel A, Reartes W. . Int J Bifurcat Chaos. 2012;22:109-29.
- Li YQ, Jiang WH, Wang HB. . Anal Appl . 2012;387:1114-26.
- Campbell SA, Leblanc VG. . J Dyn Diff Equat. 1998;10:327-46.
- Luongo A, Paolone A, Egidio AD. and resonant Hopf bifurcations . Nonlinear Dynam. 2003;34:269-91.
- Xu J, Chung KW.Double Hopf bifurcation with strong resonances in delay systems with nonlinerities . Math Probl Eng. 2009:1-16.
- Broer HW, Dijk RV, Vitolo R. resonances in quasi-periodically driven oscillators for , P. International Conference on SPT Otranto. 2007;47:71-80.
- Revel G, Alonso DM, Moiola JL.Interactions between oscillatory modes near a 2:3 resonant Hopf-Hopf Bifurcation . Chaos. 2010;20:1-8.
- Saleh K, Wagener F.Semi-global analysis of periodic and quasi-periodic normal-internal and resonances . . 2010;23:2219-52.
- Wang W, Xu J.Multiple scales analysis for double Hopf bifurcation with resonance . . 2010; 66:39-51.
- Hadian J, Nayfe AH. . J Sound Vib. 1990;142:279-92.
- Yang XL, Sethna PR. Local and global bifurcations in parametrically excited vibrations nearly square plates. Int J Nonlin Mech. 1991;26:199-220.
- Zhang W, Yu P, Liu ZM. . . 2014;24:245-68.
- Zhang W. . J Sound Vib. 2001;239:1013-36.
- Awrejcewicz J, Krysko VA. . Int J Bifurcat Chaos. 2002:12:1465-1513.
- Awrejcewicz J, Krysko AV. Analysis of complex parametric vibrations of plates and shells using Bubnov-Galerkin approach. Arch Appl Mech. 2003;73:495-504.
- Yao MH, Zhang W. -Type multipulse orbits and chaotic dynamics of a parametrically and externally excited rectangular thin plate . J Bifurcat Chaos . 2007;17:851-75.
- Zhang JH, Zhang W, Yao MH, et al. . Int J Nonlin Sci. 2008;9:381-94.
- Akour SN, Nayfeh JF.Nonlinear dynamics of polar-orthotropic circular plates . Int J Struct Stab Dy. 2006;6:253-68.
- Zhou Y, Zhang W. Double Hopf bifurcation of composite laminated piezoelectric plate subjected to external and internal excitations. Appl Math Mech Engl. 2017;38:689-706.
- Chia CY. Non-linear Analysis of Plate. McGraw-Hill; 1980.