Research
, Volume: 12( 2) DOI: 10.37532/2320ââ¬â6756.2023.12(2).258Correlation Method for Finding Gravitational Waves in LIGO Data
- *Correspondence:
- Maxim Saveliev Institute for Safety Problems of Nuclear Power Plants of the NAS of Ukraine, Ukraine,E-mail:m.saveliev@ispnpp.kiev.ua
Received date: 1-February-2023, Manuscript No. tsse-23-91320; Editor assigned: 3-February-2023, PreQC No. tsse-23-91320 (PQ); Reviewed: 7-February-2023, QC No. tsse-23-91320 (Q); Revised: 10-February-2023, Manuscript No. tsse-23-91320 (R); Published: 13- February-2023, DOI. 10.37532/2320–6756.2023.12(2).258
Citation:Saveliev M. Correlation Method for Finding Gravitational Waves in LIGO Data, J Space Explor.2023; 12(2).258. ©2023 Trade Science Inc
Keywords
Abstract
The method for finding the signal from the Gravitational Wave (GW) in the interferometrical data of the Laser Interferometer Gravitational-Wave Observatory (LIGO) is demonstrated on the test example of the gravitational event GW150914. The method is based on the use of correlation analysis, reasoning from the fact that the shape of the signal to be found is known, as well on the use of computational statistics methods. The developed method was applied for the search for signals in the LIGO data for a 32 seconds timeframe inside standard data block of 16 s prior and 16 s after the GW150914 event. The performance of the method and its advantages for the analysis of signals in a noise are shown. The paper includes analysis of possibility of the existence of other useful signals in the noise signal where the chirp of the event GW150914 was detected and risk.
Gravitation waves; LIGO; Noise signal; Correlation analysis; Computational statistics; Gravitational background
Introduction
After the discovery signals from the accelerated merger of astronomical objects by LIGO-VIRGO laboratories and announcements of the birth of a new science-gravitational astronomy, a lot of effort, both theoretical and experimental, was spent for searching gravitational background [1]. The idea is developed that we exist in an environment of constantly existing gravitational waves, similarly to the background of electromagnetic radiation. Experimental searches for manifestations of such a background mean that in real very complex LIGO signals it is necessary to find components that could be identified as gravitational background signals. Such searches have so far ended in nothing. More precisely, by estimates of the characteristics of potential sources of background gravitational waves based on the capabilities of modern equipment and the fact that no manifestations of such a background were found. In this regard, it should be emphasized that in those searches, the searched signals should have a Signal-to-Noise-Ratio (SNR) ≥ 4 [2]. There could be two reasons for a negative result of the searching. The first is that expected events are rare and all of them in the analyzed data series (series O1-O3) have already been identified in the search for gravitational events [3-5]. The second is that the signals of the type of expected gravitational background in principle cannot be detected by existing methods of their search, in which the signal is carefully filtered from the dynamic components. Sinusoidal oscillations of variable frequency and amplitude (chirps) has already been detected before the search for the gravitational background. Therefore, the search for other different templates in the filtered and already tested for chirps signals in principle cannot give new information, unless some chirps were accidentally missed. In fact, when searching for the gravitational background, in the task of finding additional signals (associated with gravitational waves), it is necessary to look for them in the noise signal, when these additional signals have a signal-to-noise ratio less then 4. However, situations arepossible, where signal amplitude is such that SNR<1. So, the search for such signals in those works was not put in principle. To date, there are theoretical limitations on the ability to detect a useful signal in Gaussian noise, which is the basis of a series of ISO 11929 standards [6]. In this (ISO 11929) ideology it is accepted that the presence of signals at certain minimum signal-to-noise ratios can be detected only statistically as exceeding the amplitude of the noise signal in certain areas relative to its average level. As far as the authors know, the search for signals in LIGO data, based on such (ISO 11929) statistical analysis approaches, was not performed.
Research Methodology
From the standpoint of ISO 11929, all noise search tasks can be divided into two groups. In the first group, a relatively weak signal against the background of noise is already directly visible, and the question is to determine its parameters. In the second group, the signal is not directly visible and the presence of the signal is defined as the presence of some additive to background noise. This situation is regulated by a series of ISO 11929 standards. But it is possible to consider an intermediate situation, when the signal exists, but practically do not differ from the noise, as, for instance, in the left part of graphs. Analysis of this situation, when the signal is already disappearing in the noise, and is the main subject of research in this paper (FIG. 1).
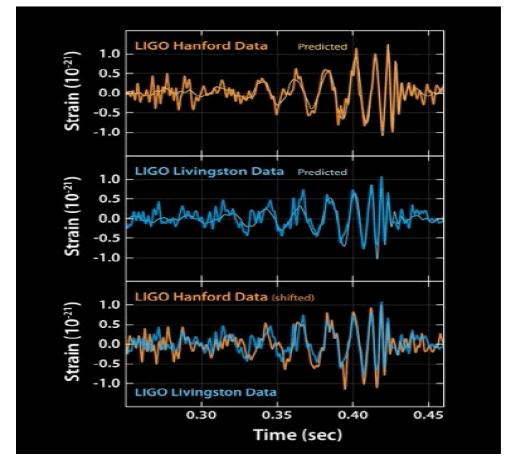
Figure 1: The image from the LIGO, which demonstrates the appearance of the gravitation wave signal: A part of a sinusoid with changing period and amplitudes.
Therefore, this paper proposes a method for finding signals of low-intensity gravitational waves, including SNR ≤ 4. There is a reason to believe that the method of chirps finding, described in, which performs in-depth filtering of various kinds of parasitic signals, cleans up the gravitational background [7, 8]. In any case, those works that attempted to find the gravitational background in real signals contain, in our opinion, internally contradictory presumption. It can be considered proven that in the process of merging of compact astronomical objects at the last moment bursts of a gravitational field of sufficient amplitude are formed in the form of so-called chirps - packets containing up to ten periods of variable frequency and amplitude [9,10]. Such chirps have been found and in the principles of finding such formations in real signals used by LIGO were describes [11]. The example of event GW150914 describes a method of filtering LIGO equipment signals from various parasitic components and the end result: A clearly visible signal against a background of uniform Gaussian noise. However, the statement that after filtering the noise signal against which the chirp is observed is Gaussian automatically means that such a signal is a random set of independent numbers and cannot contain regular components such as lowamplitude sinusoidal chirps. Namely this type of background signals was analyzed to find chirps or other manifestations of a variable gravitational field. In fact, the LIGO signals of the O1 cycle, in which GW150914 was detected, were analyzed in terms of finding in them features that are additional to the already identified gravitational events. And these features were sought against a background that was considered as Gaussian noise [12]. That is, the signal-to-noise ratio for the expected signals must exceed one at least. The general scheme for finding the signal from the gravitational wave in the signal from the LIGO interferometric equipment is as follows. For some time, a LIGO signal is registered, which in the absence of known gravitational events can be considered as background. This signal is quite complex, with powerful parasitic components. Next, this general signal is analyzed for the presence of a useful signal. Note that the useful signal is very weak, hidden in the noise and to detect it special complex methods of analysis are used. After detecting such a signal, one of the main ways to prove the reality of its origin from the gravitational event is to compare it with independent measurements. As a rule, the real signal of the gravitational wave is a signal of a certain shape, registered simultaneously by two independent gravitational observatories, in this case LIGO-Hanford and LIGO-Livingston. The problem is that the signals from gravitational waves are very weak, they are difficult to distinguish against the background of noise. There are theoretical and experimental limits of sensitivity of equipment and methods of data analysis (SNR ≤ 4). Consequently, signals whose intensity is below the sensitivity limit will not be identified, even if they come to the detectors. Therefore, increasing the sensitivity of the system, in this case the methods of analysis, is a fundamental task. It should be also kept in mind that gravity signals already detected by matched filtering correspond to some model of the process that generates them, namely the model of merging of compact astrophysical objects. On the basis of such models templates are created-theoretically expected signals of a certain shape which have been successfully found. But the absence of manifestations of such templates in the general signal does not mean that the existence of gravitational signals of another form is impossible, i.e. on the basis of other models. A generalized search with minimal assumptions about the shape of the signal was made in and nothing was found [13]. Not found at the existing sensitivity of the equipment and noise level yet. Therefore, the search should be continued with both high-sensitivity equipment and other methods of analysis of available data. Perhaps it would be correct to set the task of finding in LIGO signals deviations from some unknown base signal, which may be the model noise signal. In the following chapters, we will describe the general algorithm of our processing. Then we apply it to the data of the LIGO observatory and show that the results obtained are equivalent to the standard LIGO results for the event GW150914 (FIG. 1). Finally, we will try to take a more general look at the results obtained in order to evaluate the possibilities of the proposed correlation method for advanced analysis of data obtained on LIGO-VIRGO interferometers. However, the statement that after filtering the noise signal against which the chirp is observed is Gaussian automatically means that such a signal is a random set of independent numbers and cannot contain regular components such as lowamplitude sinusoidal chirps. Namely this type of background signals was analyzed to find chirps or other manifestations of a variable gravitational field. In fact, the LIGO signals of the O1 cycle, in which GW150914 was detected, were analyzed in terms of finding in them features that are additional to the already identified gravitational events. And these features were sought against a background that was considered as Gaussian noise. That is, the signal-to-noise ratio for the expected signals must exceed one at leastThe general scheme for finding the signal from the gravitational wave in the signal from the LIGO interferometric equipment is as follows. For some time, a LIGO signal is registered, which in the absence of known gravitational events can be considered as background. This signal is quite complex, with powerful parasitic components. Next, this general signal is analyzed for the presence of a useful signal. Note that the useful signal is very weak, hidden in the noise and to detect it special complex methods of analysis are used. After detecting such a signal, one of the main ways to prove the reality of its origin from the gravitational event is to compare with independent measurements. As a rule, the real signal of the gravitational wave is a signal of a certain shape, registered simultaneously by two independent gravitational observatories, in this case LIGO-Hanford and LIGO-Livingston. The problem is that the signals from gravitational waves are very weak, they are difficult to distinguish against the background of noise. There are theoretical and experimental limits of sensitivity of equipment and methods of data analysis (SNR ≤ 4). Consequently, signals whose intensity is below the sensitivity limit will not be identified, even if they come to the detectors. Therefore, increasing the sensitivity of the system, in this case the methods of analysis, is a fundamental task. It should be also kept in mind that gravity signals already detected by matched filtering correspond to some model of the process that generates them, namely the model of merging of compact astrophysical objects. On the basis of such models templates are created theoretically expected signals of a certain shape which have been successfully found. But the absence of manifestations of such templates in the general signal does not mean that the existence of gravitational signals of another form is impossible, i.e. on the basis of other models. A generalized search with minimal assumptions about the shape of the signal was made in and nothing was found. Not found at the existing sensitivity of the equipment and noise level yet. Therefore, the search should be continued with both high-sensitivity equipment and other methods of analysis of available data. Perhaps it would be correct to set the task of finding in LIGO signals deviations from some unknown base signal, which may be the model noise signal. In the following chapters, we will describe the general algorithm of our processing. Then we apply it to the data of the LIGO observatory and show that the results obtained are equivalent to the standard LIGO results for the event GW150914. Finally, we will try to take a more general look at the results obtained in order to evaluate the possibilities of the proposed correlation method for advanced analysis of data obtained on LIGO-VIRGO interferometers.
Correlation method of analysis
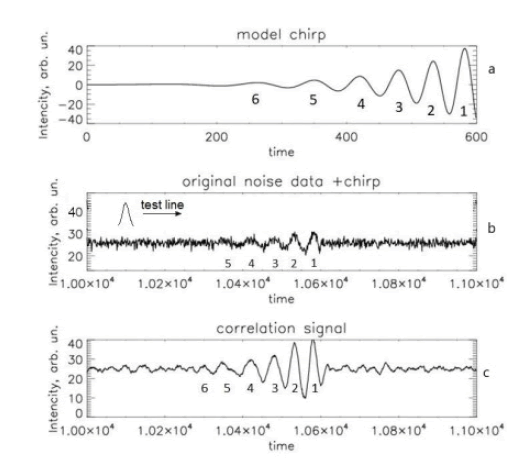
This paper proposes a method for detecting a signal from a gravitational wave, also based on the fact that the shape of such a signal is known. So, the main assumption is if there is a gravitational wave, the signal must be in the form of at least one sinusoid’s halfperiod. The method of analysis proposed in the paper is based on the ideas of computational statistics, and was previously developed for the analysis of gamma spectra in gamma spectrometry, and for the analysis of weak, noise-hidden lines in X-ray powder diffraction where it showed high efficiency [14-16]. The idea of the method is as follows. There is a noise-like signal, which in our case of consecutive measurements of signal intensity will be a regular series of numbers tied to the time of their receipt (FIG. 2). Suppose further that at some moment of time the detectors received a "useful" signal. For simplicity, we assume that this signal has the shape as in FIG. 2, it means have several periods of sinusoid with increasing frequency and amplitude. Let is now create a test function in the form of a bell (Gaussian line). If we now scan a series of measurements with this test function, similar to the useful signal, calculating the correlation coefficient at each step, we obtain a new series of data in which increased values of the correlation coefficient will be observed when the test signal coincides with the useful signal. If you look at FIG. 1 and 2, it is clear that its a separate part with a size in the half-cycle, just and will be such a test bell-shaped signal, the coincidence with which must be sought in the real signal. Next, the obtained correlation series is analyzed, which as shown demonstrates a higher sensitivity to the presence of signals, similar to the test line, hidden in the noise. Indeed, FIG. 2 shows only the first three or four peaks of the chirp, the amplitude of the others is already equal to the noise. However, all five or six chirp periods have been reliably detected in the correlation spectrum and in the picture of its wavelet transform. Thus, signals with an intensity at the noise level are actually detected. We emphasize that in the described method, in contrast to the matching template, the search is not for the chirp as a whole, but for individual bell-shaped (sine wave half-cycle) signals, and the chirp in this search will appear as a series of such bell-shaped signals. Note also that the proposed method effectively removes random high-frequency noise and on the correlation spectrum it no longer exists, and the remaining noise track is only the small peaks of correlation of the test line with model Gaussian noise (FIG. 2). It is clear that such noise does not contain the necessary information and in this case are incorrect and determine the sensitivity of the method. In further analysis, it should be removed.
Results & Discussion
Analysis of LIGO data
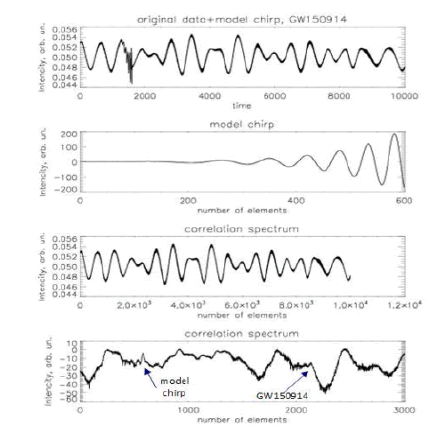
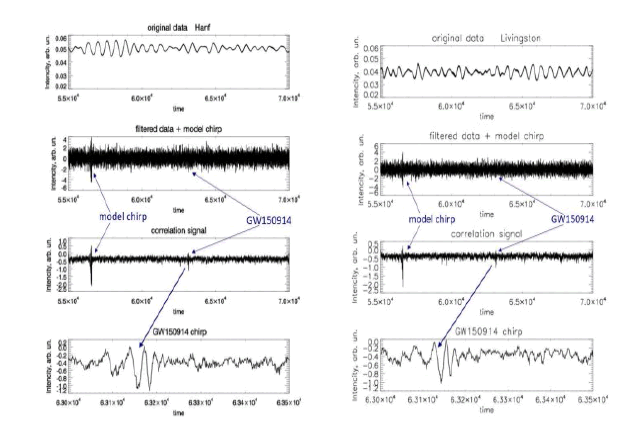
The test of the proposed correlation method was performed on the known example of the gravitational event GW150914. As in the classical approach, data from the Hanford Observatory, Washington, and the Livingston Observatory, Louisiana, will be analyzed. Let’s make some estimates for the convenience of further analysis. It is believed that the gravitational wave was recorded at September 14 2015, 09:50:45 UTC. The duration of the event is about two seconds. However, for the convenience of analysis, it is more convenient to estimate the occurrence of the event in the sequence numbers of the array elements of the available regular data, as all graphs are given in the array element numbers. The LIGO site gives a signal (data array) lasting 32 seconds. Recording continues from September 14 2015, GPS time 1126259447 UTC. The data sets are organized so that the gravitational event is in the middle of this series of data lasting 32 seconds. That is, the event was recorded on about 16th second. For example, for Hanford data, the total data set is 131,072 elements. The event on the 16th second is in the middle of an array of data with the size 131,072 elements. So, we need to look for the necessary signal somewhere between 55,000 and 70,000 elements. The situation is similar for data from Livingston. FIG. 3 shows, as an example, a typical appearance of a signal received in LIGO equipment. It is clear that the signal is a noise-modulated sine wave. The signal of this sine wave has a certain thickness, which is the result of the presence of high-frequency components, among which you need to look for the gravitational signal. The given signal contains event GW150914, and also for control to it the model chirp which form and amplitude are close to a real signal of event GW150914 is added. Below the chirp signal the signal obtained after correlation processing is shown. On such a graph, the manifestations of both model and real chirps are not visible. However, on a larger scale in FIG. 3, you can already see some features in places where both the control chirp and the event GW150914 chirp are located hub.
Figure 3: Source data analysis, event GW150914, without digital filtering. From top to bottom: input signal; model chirp; correlation signal; part of this correlation signal on a large scale, with addition of a model chirp.
Data filtering
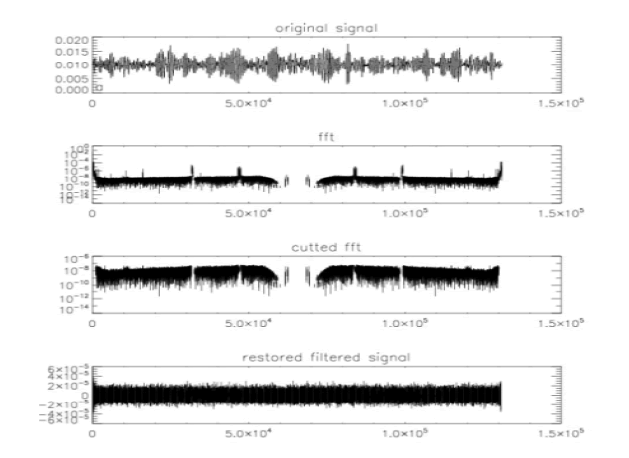
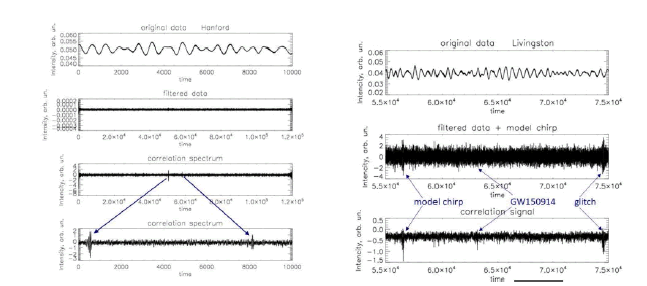
However, it is clear that such graphs do not look convincing and are not suitable for real searches for signals from gravitational events by the proposed method. In order to find a useful component in the form of a chirp in such a signal, it is necessary first to filter out powerful parasitic periodic components. We will do it by following (FIG. 4). Let’s perform the Fourier transform of the general signal (FIG. 4). The Fourier transform pattern clearly shows a number of powerful peaks that are considered as manifestation of the presence of periodic signals such as vibration of the equipment and so on [17, 18]. These peaks are obviously parasitic and must be filtered out. In the approach used, these components in the Fourier spectrum simply assume zero. The Fourier spectrum after such primary filtration is shown in FIG. 4. Of course, care must be taken not to filter out the spectral components associated with the useful signal. Such filtering is imperfect in the sense that it is not automated and, as a first approximation, filters only obvious parasitic peaks. It can be continued if you determine the parasitism of other weaker peaks. On the other hand, careful automated filtering using various digital filters can lead to the filtering of unknown useful signals , which we are actually looking for when analyzing the gravitational background. After the inverse Fourier transform, we obtain a signal free of such powerful periodic components, which already has the appearance of noise-like and in which the signal can be searched by the proposed correlation method.
Figure 4: Fourier transform filtration (FFT). Event GW 150914. Data from the Hanford Observatory. From top to bottom: input signal; his Fourier transform; FFT signal after filtering the most powerful periodic components visible in it; restored input signal.
Search for gravitational events in the LIGO Signal
The proposed correlation method after filtration of parasitic components was able to find the event signal GW 150914 in both LIGO-Hanford data and LIGO-Livingston data (FIG. 5). However, this paper had another goal to propose a method for the analysis of a noise-like signal outside the chirp of a gravitational event. In general, the problem of finding such signals, as in the case of known gravitational events, is not to misidentify the useful signal due to random matches in the signal. Today, a reliable method used by LIGO collaboration is to compare signals from two independent observatories. Simultaneous random appearance of the same chirps in the signals from different detectors is considered statistically impossible. Most likely, this criterion should be applied in our situation. Note that the noise level after filtering remained so high that in the noise-like signal (FIG. 5), obtained after filtration, there are no real manifestations of the gravitational event.
Figure 5: Correlation analysis of event GW150914 data. On the left are data from the Hanford Observatory, and on the right are data from the Livingston Observatory. From top to bottom: input signal with added model chirp; the same signal after filtering out the most powerful periodic components visible in its Fourier spectrum; correlation signal, which shows the left model chirp and real chirp of gravitational wave; part of this signal on a large scale after correlation processing. Test signal consists of 20 data array elements.
Search for gravitational background and other features
In standard approach after filtering the input signals, a stationary noise should ideally remain, above which a useful signal is seen. This situation can be described as follows. As a result of filtering of parasitic signals, the original sine wave turned into a noise-like signal, against the background of which the corresponding chip is easily located (FIG. 5). We emphasize that in the adopted LIGO search methods for the reliability of the result it is assumed that the signal-to-noise ratio should exceed 4. Because the LIGO search did not detect gravitational background signals with such an SNR, the required hypothetical gravitational background signals should have less SNR up to the level of these residual noises [19]. Therefore, in principle, they cannot be expected to be detected by the methods used in, because they can only analyse signals that are visible against the background of noise. But you can try to detect them by the proposed correlation method, which allows you to find signals with a signal-to-noise ratio of 1 (FIG. 2). The result of this analysis for the existing data set with a duration of 32 s is presented in FIG. 6, for a test signal with a width of 14, i.e. approximately in the frequency range of the chip GW150914. On the left are Hanford’s data, on the right is Livingston ones. As can be seen from the graph in FIG. 6 for Hanford, no bursts that would stand out on this graph, except for the model and real signal from GW150914, are not observed.
Figure 6: Analysis of GW150914 data for 32 seconds (16 s before GW and 16 s after). Left: Data from the Hanford Observatory, test line width=14. From top to bottom: part of the input signal; the full (32 s) signal after filtering the most powerful periodic components visible in its Fourier spectrum; correlation signal; part of this large-scale correlation signal showing the model chirp and the gravitational wave chirp. Horizontal axis is a time in units of elements number. Right: a sample from the Livingston Observatory, where a model chirp, a GW150914 chirp, and a glitch parasitic burst were observed.
In Livingston’s data, an additional burst-like signal was detected in the area of 74,000th elements. Because it does not have the counterpart in the Hanford signal, it was recognized as a parasitic glitch. Therefore, even if our proosed method is at least 2 times more sensitive then the standard, we also did not find the required background signals. We emphasize once again that the search result depends on the parameters of the test line. In this case, this means that no additional (up to chirp) signals were detected when searching in the chirp frequency range (approximately 85 Hz-256 Hz). The signals of the expected gravitational background in terms of their search can be divided into two groups:
• The total signal from many uncorrelated sources of gravitational waves should be in the form of noise. Such a signal can be sought as manifestations of correlated changes in the noise value in different detectors;
• If the number of sources is not very large, the gravitational background will have the form of individual packages of sinusoidal oscillations, the duration of which is less than the observation period. The search for such signals will be similar to the search for chips. It means the search for the appearance of sine waves of a given frequency simultaneously in several detectors.
Conclusion
A method for analyzing the signals of gravitational observatories to search for signals from gravitational waves in them is proposed. The method is based on the use of correlation analysis with using computational statistics methods to calculate correlations. The possibilities of the method are demonstrated on the data of the LIGO observatory for the gravitational event GW150914. The most interesting feature of the proposed method is its possibility to detect separate bursts of the “unmodelled” gravitational events. The negative results of the careful analysis of the available data of the O1-O3 series for searching gravitational background clearly show that if the required gravitational background signals exist, their amplitude should be much smaller than SNR=4. Most likely they should be hiding in the noise. In our study, the manifestations of sinusoids of continuous gravitational background waves at intervals of 32 s around the event GW150914 were also not found. That is, according to the results of the analysis we can conclude that if such a gravitational background does exist, its intensity is much lower than the existing noise level, taking into account the increased in several times the sensitivity of the method of analysis used. However, with respect to chirp-type signals whose amplitude corresponds to SNR<4, the situation is different. If you filter the output signal as it does LIGO, and to apply the proposed correlation method to such a signal, then chirps and individual bursts with SNR about 1, if any, will be found in it
References
- McLaughlin M, Thorpe JI. Gravitational-Wave Astronomy and Beyond: A view across the gravitational wave spectrum.2020
- Caudill S, Kandhasamy S, Lazzaro C, et al. Gravitational-wave searches in the era of Advanced LIGO and Virgo. Mod Phys Lett A. 2021;36(23):2130022.
- Abbott BP, Abbott R, Abbott T, et al. GWTC-1: a gravitational-wave transient catalog of compact binary mergers observed by LIGO and Virgo during the first and second observing runs. Physical Review X. 2019;9(3):031040.
- Abbott R, Abbott TD, Acernese F, et al. GWTC-2.1: Deep extended catalog of compact binary coalescences observed by LIGO and Virgo during the first half of the third observing run. arXiv preprint arXiv:2108.01045. 2021.
- Abbott R, Abbott TD, Acernese F,et al. GWTC-3: compact binary coalescences observed by LIGO and Virgo during the second part of the third observing run. arXiv preprint arXiv:2111.03606. 2021.
- Technical Committee ISO/TC 85, Nuclear energy. Subcommittee SC 2, Radiation protection. Determination of the Characteristic Limits (decision Threshold, Detection Limit and Limits of the Confidence Interval) for Measurements of Ionizing Radiation--fundamentals and Application. ISO; 2010.
- Abbott BP, Abbott R, Abbott TD,et al. Characterization of transient noise in Advanced LIGO relevant to gravitational wave signal GW150914. Class. Quantum Gravity. 2016;33(13):134001.
- Abbott BP, Abbott R, Abbott TD, et al. A guide to LIGO–Virgo detector noise and extraction of transient gravitational-wave signals. Class. Quantum Gravity. 2020;37(5):055002.
- Scientific LI, Abbott BP, Abbott R, et al. Search for the isotropic stochastic background using data from Advanced LIGO’s second observing run. Physical Review D. 2019;100(6):061101.
- Abbott R, Abbott TD, Acernese F, et al. All-sky search for short gravitational-wave bursts in the third Advanced LIGO and Advanced Virgo run. Physical Review D. 2021;104(12):122004.
- Abbott BP, Abbott R, Abbott TD, et al. Observation of gravitational waves from a binary black hole merger. Physical review letters. 2016;116(6):061102.
- Abbott BP, Abbott R, Abbott TD, et al. All-sky search for short gravitational-wave bursts in the first Advanced LIGO run. Physical Review D. 2017;95(4):042003.
- LIGO Scientific Collaboration, Virgo Collaboration, Kagra Collaboration. All-sky search for continuous gravitational waves from isolated neutron stars in the early O3 LIGO data. Physical Review D. 2021;104(8):1-28.
- Moore DS, McCabe GP. Introduction to the Practice of Statistics. WH Freeman/Times Books/Henry Holt & Co; 1989.
- Scorbun AD, Panasyuk MI. Resolution of low-intensity lines in gamma spectra. Probl. Bezpek. At. Elektrost. Chornobyl. 2008;9:125.
- Skorbun AD, Gabielkov SV, Zhyganiuk IV, et al. Method of X-Ray Diffraction Data Processing for Multiphase Materials with Low Phase Contents. arXiv preprint arXiv:2001.02045. 2019.
- Covas PB, Effler A, Goetz E, et al. Identification and mitigation of narrow spectral artifacts that degrade searches for persistent gravitational waves in the first two observing runs of Advanced LIGO. Physical Review D. 2018 ;97(8):082002..
- Callister III TA. Searching for the Astrophysical Gravitational-Wave Background and Prompt Radio Emission from Compact Binaries (Doctoral dissertation, California Institute of Technology).
- Abbott R, Abbott TD, Acernese F, et al. All-sky, all-frequency directional search for persistent gravitational waves from Advanced LIGO’s and Advanced Virgo’s first three observing runs. Physical Review D. 2022;105(12):122001.