Research

, Volume: 12( 1) DOI: 10.37532/2320-6756.2023.11(4).334

• View PDF
• Download PDF

Asymmetry in the Real Number Line and: A Proof that π + e is an Irrational Number

*Correspondence:

Alexander C. Sarich Independent Researcher, USA, E-mail: sarichac@vcu.edu

Abstract

The following document is provided as a preliminary discussion regarding certain equivalence properties which arise between Mathematical Asymmetry and operations on Irrational numbers. The purpose for writing this preface is to offer the reader, if one so chooses to continue, certain advice and warnings about this reasoning. To which, I first must indulge that upon peer review, I have become acutely aware of these problems, but due to current invested interest and work regarding the field of Irrational numbers, it is my belief that there may exist pieces herein that are useful in a philosophically reductionist capacity. Of note, that forcefully this paper disregards the use of the Archimedean Property; where, without strong proof, asserts this to be a necessary conclusion since the Reals comprise a larger cardinality than the Rationals. Second, though the Rationals are assumed to be Dense on themselves, they are defined as not Dense on the Reals and as such is claimed that any arbitrary consecutive ordering of Rationals in a continuous interval on the Reals requires the Rationals to be equally spaced. Lastly, the application of these concepts to the problem of π+e implies contradiction if these assumptions are disputed. From the introduction onward, no statements have been revised to supplement these claims; instead, a more intensive and sophisticated undertaking has since begun in parallel, which ought to eventually supplement the weaknesses of this paper. As such, it is clear that the field of Irrational numbers, R/Q and techniques for simplifying analysis, is still a very open problem in Mathematics.

Keywords

Irrational numbers; Real number

Introduction

The set of all Real numbers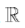 , consists of all Rational numbers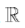, being any ratio of two Integer numbers that does not divide by 0. All other Real numbers that are not a Rational number are contained in the set of Irrational numbers,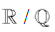. These two subsets comprising all of the Real numbers are known to have distinct cardinalities of differing magnitudes of infinity [1]. When a consecutive ordering of all Rational numbers is established, whereby any unique Rational number can be shown to be disconnected from all other Rational numbers [2], a theorem regarding asymmetry on the Real number line is established. This theorem simplifies the necessary requirements to prove that the summation of two known Irrational numbers is Rational or Irrational.

With great respect and admiration to the development of Irrational number analysis and considerations on the Real number line; through the works of Richard Dedekind and Georg Cantor, there appears to be a currently (as well as I am aware) unstated theorem regarding the construction of the Real number line. To the best of my abilities at present, the following document is offered as an ntroductory discussion on how this conclusion arises to verify this theorem, and provides an example to better illustrate application. It was during the early spring months of 2020 while working through equilibrium problems that I first became curious about the construction of Irrational numbers. I had spent time studying Set Theory in Richmond the Fall earlier, dwelling on the nature of infinite sets and the axioms by which Kurt Gödel was able to prove his Incompleteness Theorem when I began experimenting with the logic of equilibrium. I had wanted to prove to myself whether it was possible for a perfectly made sphere to balance on top of a perfectly built cone. If there was only one exact point of contact between the tip of the cone and the edge of the sphere, with no external forces other than a constant downward force, would it be possible for this sphere to balance forever? My initial conclusion is one of common sense, that the equal balance on all sides of the sphere would cancel out and the objects would be in perfect equilibrium, the sphere would never fall. To prove this, the answer seemed to be as straightforward as translating every threedimensional point on the sphere to a single point on a line, and see if that length making up the volume, could be perfectly cut in half. When I set the volume of the sphere to four-thirds times’ π times the radius-cubed, forcing the radius to be a Rational number, the length of the line landed on an Irrational number. Then, it became clear that to show that if this line could be cut in half perfectly, we would need to verify that every Irrational number is equal distance from the first Rational number greater than it and the first Rational number less than it. At this point, one may be concerning themselves with the same dilemma that had been facing myself at the time, either the infinity of points between this halfway point is always infinite and therefore the same, or that if this halfway point is offset, there must be a way to show why that is the case. Then, after a considerable amount of time pouring over possibilities, considerations, meditations, and research, it appeared logical that the only case is that the Irrational numbers comprise a naturally unbalanced relationship to the Rational numbers. At the time of this writing, about sixteen months have passed since I first proved this theorem to myself. As well, there appears enough in this to at least conclude that π+e must be an Irrational number. Since this proof that π+e is an Irrational number directly follows from this Theorem, I believe it is in the best interest of those considering the argument to continue on with utmost scrutiny and skepticism. The purpose may indeed appear central to a single problem, but elseward symbolizes instead the scope of Mathematics as a field which will forever require updates and further development.

The Real Number Line and Infinities

As a general concept, those who study the most elementary of Mathematics are aware that the scope of all Real numbers can be broken down into smaller subsets of those numbers. In a simplified explanation, this happens because we start with a simple idea of quantifying. We start with the number 1 which can be analogous to something. If we have several somethings, we are just putting 1 and 1 and so on together; so we designate larger numbers for that. If we have none of whatever that something is, then we essentially have no 1’s and that gives us nothing, which is 0. If we keep adding 1’s forever, then we get a number that is going to be ∞. Thus, if we start at 0 and allow ourselves to add any amount of 1’s, we have addition, multiplication, and the Natural numbers, N. We know that if we keep adding 1’s, we end up at infinity, and since we can count by 1’s, then we should have an easy time just calling this set of numbers Countably Infinite. Then, if we start at any number and start removing 1’s, at some point we reach 0, and if we remove 1 from 0 we get −1. If instead we said 0−1=0, and already established that 0+1=1, then adding the left and right sides of both equations gets (0−1)+(0+1)=0 and 0+1=1. But of course, 0=1 is a contradiction; so we need negative numbers to avoid this problem. So, if we include all the positives and negatives we get the Integers,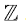. Is this a different infinity from Countably Infinite? Well, if we define some function where every consecutive even Natural number maps to every consecutive Natural number and every odd Natural number maps to every consecutive negative number, then we can still count analogous to the Naturals. So the Integers and Naturals are both Countably Infinite. More or less, we now also have all numbers starting with 0, 1, ∞ and how they add, multiply, and subtract. What happens if we start dividing these numbers? For one thing, let us just ignore any possibility of dividing by 0, as this falls outside the scope of this argument; though interesting discussion is made on the topic when, for example, reading through the work of George Boole [3]. Regardless, if we consider the set of all possible Integers and for every Integer every possible Integer that is not 0 that can divide it, we end up with the Rational numbers,; this will also be Countably Infinite. A way to show this would be to setup a 2X2 table where every row is a Natural number and will be the numerator and every column is a Natural number and will be the denominator. By following these numbers in a diagonal path, they can be mapped to the Naturals and are therefore also Countably Infinite. All that is missing are all the numbers that are between two Rational numbers but cannot be obtained by dividing an Integer by another Integer that is not 0. These can be shown to be there through a Dedekind Cut and are all the Irrational numbers, 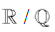[4]. If we assume that the Irrational numbers are also Countably Infinite, we would ultimately end up with a contradiction and this was proven eloquently when Georg Cantor introduced his Second Diagonalization Argument [1]. Essentially, if we try to apply the same method as we did with the Rational numbers, we will forever and always end up with at least one Irrational number not accounted for, and if we rewrite a list to include that unaccounted for Irrational number, we will again find another number unaccounted for. Therefore, the set of all Irrational numbers is not Countably Infinite, it is some larger infinity, to which we can simply call Uncountably Infinite.

Now, what we can take to be true is that the respective sets of the Natural, Integer, and Rational numbers all have the same infinity. As a whole they are all Countably Infinite and that this quantity of the sets is referred to as their cardinality. This is written where if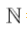 ={0, 1, 2, 3, ...} is how we show what the Natural numbers are, then,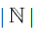being the cardinality, will be the quantity of all the numbers contained therein. Since the cardinality of the Irrational numbers, 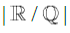is a larger infinity than the Rationals, we can map all the Rationals to the Irrationals and then have the rest of the Irrationals map to themselves, thus acquiring all of the Real numbers. What we end up with is a simple statement that compares these sets of numbers:

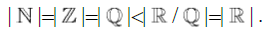
SSince the Natural numbers and Rational numbers are in total both Countably Infinite, suppose we look exclusively at all Rational numbers of the typ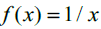ewhere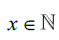Then the set of all possible values for 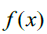will still be Countably Infinite and also a subset of the Rationals. So we have a set of Rational numbers between 0 and 1 including 1 that can be mapped to all the Rational numbers and hence all the Natural numbers and hence the 8th number of the Natural numbers and all the numbers less than, such which can conversely be mapped to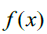Then if we can map 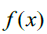to the entirety of the Rationals, if we also consider all the numbers not contained in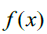between 0 and 1 we get a set of Rational and Irrational numbers which can be mapped to all the Irrational numbers which can then be mapped to all the Real numbers, which means the cardinality of all the numbers not contained in 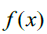between 0 and 1 will be Uncountable Infinite. Next, suppose we consider a second function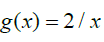where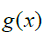 is taken to be only those values which fall between 0 and 1 including 1. Then we have another set of Rational numbers that is some subset of 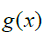being equal to some subset of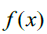and nonempty. If we then consider the union of all the numbers in 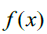and 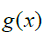we get a set that we can map to the Rational numbers; where, all the numbers from 0 to 1 not in this set will be all the Irrational numbers from 0 to 1 and all the Rationals not obtainable from 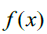and 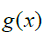which can still be mapped to the Real numbers. If we continue in this way, we can write every single number between 0 and 1 that is obtainable through the form 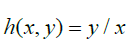where x,This gives us all the Rational numbers from 0 to 1, with every number not contained in 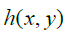from 0 to 1 being an Irrational number. If we give this same setup for 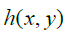from 1 to 2 or with any generalized boundary condition of Rational numbers, we ultimately end up with the same situation. That 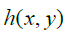gives all the Rational numbers in that range and the rest will be the Irrational numbers. We can write this in a more succinct manner. Suppose we let A be any arbitrary interval of the Reals such that A[a,b]; 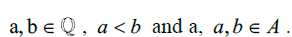Then no matter what a and b are chosen to be, as long as they are Real numbers and a is less than b, there will always be some number that is a y/x ratio distance between a and b. What we can do with this information is write out a function that gives us all the Rational numbers in any interval of A.

If 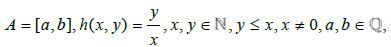then every possible solution for 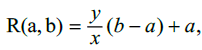contains every possible Rational number in A.

Since R must contain all the Rational numbers in A , and this can be mapped to all the Rational numbers in the Reals, no matter how small or big we make the difference between a and b , we always end up with the same set of ratios between the difference. If we consider a second set B =[c, d] analogous to A where c<a and b<d, the formula for R substituting in c and d gives us all the Rational numbers in [c,d] , which must then also contain all the rational numbers in [ a,b] . Then, if we are able to acquire all the Rational numbers for any possible interval of A using the same Countably Infinite ratio function being h(x, y)=y / x we can also get all the Rational numbers contained in a subset thereof, then the ratio difference between consecutive Rational numbers must be constant. Just as the difference between consecutive Natural numbers will always be 1, the difference between consecutive Rational numbers must also be some constant value. Now, if we take the set A and remove all solutions for R(a, b) , what we end up with is a set /AR, which translates roughly to, "all the elements in A that are not also an element of R ", with R being the set of all possible solutions for R(a, b) ; then, A/R will consist of all the Irrational numbers in A with the cardinality of this set, | A/ R |, being unaccountably Infinite. Then, since we can then map this set, A , to the set of all Real numbers, but cannot fully map all the Real numbers to the set of all possible solutions for R , then | R | contains a lesser infinity than | A/ R |.

So far, we have stated that since all Rational numbers can be expressed as the ratio of two Integer values, then the difference between any two consecutive Rational numbers will always be constant. This appears as a consequence of their construction. We have that between any two Rational numbers there must always exist some Irrational number, and that the infinity of all Irrational numbers is larger than the infinity of all Rational numbers. Since any unique Rational number can be infinitely divided, and no matter how small the difference between any two Rational numbers is, there must still exist at least some infinity of Irrational numbers between any two Rational numbers. Therefore, we can say that for any unique Rational number, there must always exist some arbitrarily small interval where the cardinality of all Rational numbers in that interval will be 1; whereas, the cardinality of all Irrational numbers in that interval will still be Uncountably infinite. This means that for any Rational number, 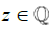, an interval containing only the Rational number, z , must have upper and lower limits being Irrational numbers. Which, if for every Rational number, there exists some small interval such that there exists only one Rational number within, then we can say that the set of all Rational numbers on the Real number line are disconnected from each other. However, unlike the Natural numbers or Integers, where the value of difference is consequently noted as always being a difference of 1, in order to consider the value of this difference between Rational numbers, to move forward, we require only to accept this as a logical consequence of their definition. That is, suppose we imagine two consecutive Rational numbers wherein no Rational number exists there between. Ignoring the impossibility of ever acquiring two such numbers, suppose we have 0 and the smallest rational number greater than 0. In theory, we might try and write this as 1/ ∞; however, this is a weak definition as this is commonly accepted to be the same as the limit of 1/ n as n approaches ∞, which is equal to 0. Since this is a function which is looking for the limit, we cannot use this as a means to describe this value. Instead, the concept here is not to quantify a value which approaches 0, but to reconcile the logical consequence that if the Irrationals are infinitely larger than the rational, and the rational always contain an equal distance between consecutive numbers, then between any two consecutive rational, there must exist at least one Irrational number there between. Not only will there be at least one Irrational number between 0 and the first consecutive Rational number after 0, but there must exist at least an infinite number of Irrational numbers in that range since any finite difference would allow a means to map the Irrationals to the Countably Infinite set of numbers. Let us instead define this value in the following way:

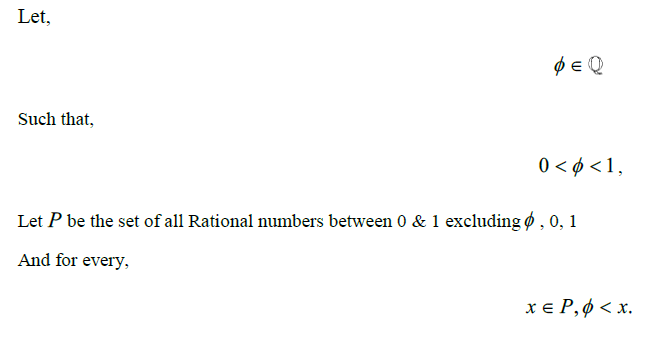
From this we have a Rational number that is greater than 0 but less than every other Rational number in P . If we say there exists some Rational number, y< , then we get a contradiction since y must either be an element of P or equal to . We can use this definition of , being the smallest Rational number greater than 0, to define the set of all Rational numbers. Similar to the method of indexing employed by Cantor [2] for consecutive Real Algebraic numbers, let us define the set of all positive Rational numbers to 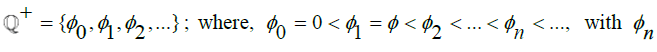with nbeing some arbitrary Rational number. Since the Rationals and Naturals comprise a Countably Infinite amount of numbers, we can index in this manner with each consecutive Rational number corresponding to some Natural number. Then, since the distance between any two Rational numbers must be constant, then we can write that difference as 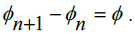Now, suppose we build an interval from 0 to where we now have a continuous set of numbers which contains no Rational numbers between the limits. Let us consider the interval [0,] being the set which contains only two Rational numbers, 0 and. What happens when we divide by 2? If is a rational number, then dividing by 2 ought to provide a Rational number; however, since /2≠0, then /2 will be some number less than and greater than 0, except the only positive Rational number less than is 0, therefore, the value of /2being an element of [0, ] means it must be an irrational number. Ultimately, we get a paradox. Instead, let us further constrain ourselves under this conception already employed. That if we are at all able to divide our Rational number by any integer amount, then that original value we set for was incorrect and that the new number must be or will be some number less than it. Thus, in order to resolve this apparent paradox of thought, we must consider this problem not from the limit values of the interval, but instead from the elements contained within.

We have so far that the set [0, ] is some continuous interval such that the cardinality is Uncountably Infinite, the only Rational numbers contained in the interval are its limits 0 and , and that the remainder of elements in the interval must be Irrational numbers. Then if no rational numbers exist in this interval except for 0 and , we have that is no longer divisible by any Integer number. However, under this restriction we can still divide by any Irrational number value, which still provides for the set to be continuous within the limits of the interval. Since we know that is the smallest Rational number after 0, we can infer that if there exists some halfway point between 0 and , it will be some Irrational number. We will define this halfway point to be 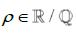such that ρ is approximately equal to /2 while remaining distinct from /2 since 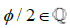. The conclusion to this problem being that in order for the continuity of the number line to exist, then the halfway point from 0 to must exist, and since this halfway point exists, then it must be an Irrational number. Which then requires that this halfway point be offset to the Rational number limits in the interval. Thus, in this reasoning we can then conclude that this interval of Irrational numbers is asymmetric to the Rational numbers.

Now, when we refer to symmetry with respect to the Real number line, we will say that for any continuous interval where there exists some point between its limits that has the same ratio distance between both points, that interval comprises symmetry. By taking our example of the consecutive sequence of Rational numbers from 0 to , noting that is the smallest Rational number greater than 0, we have that /2 cannot be a Rational number; however, for there to exist symmetry in [0, ], we would need to find some number in the interval with an equal difference from 0 and from , since the only possible solution would be /2, and since this value cannot exist by the constrains of our definition of this interval, we cannot say this interval is symmetric and therefore the interval is asymmetric. Then for any interval on the Real number line with upper and lower Rational number limits being a difference of apart, we have an Uncountably Infinite amount of elements in the interval where there exists no element which can form a symmetry with respect to its limits. Now, because we know that the ratio between consecutive Rational numbers is constant, if we consider some Irrational number in a continuous interval with upper and lower limits being consecutive Rational numbers a distance apart, we can compare this to some other Irrational number in the interval [0, ]. 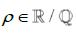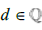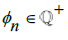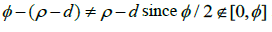In other words, suppose we have some positive Irrational number and we require being some to be the largest Rational number such that p-d∈[0,], then we know that .Then, if we have this Irrational number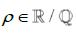and we sum with another positive Irrational number, ω, then by setting ρ 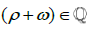,we find that the difference between ω and the smallest Rational number greater than ω must be equal tod ρ-d. Where, we can also define the number 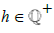to be the largest Rational number less than ω, such that 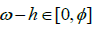Then if the sum of ω and ρ is some Rational number, then 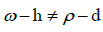since the interval [0,] contains no element which is equal difference from 0 and from. This then allows us to consider Irrational numbers as they pertain to a unique position within the interval [0, ], and that if two unique Irrational numbers, ρ and ω, do not sum to a Rational number, then there exists at least one solution to show that We will use the example of π+e to demonstrate one such method where it can be shown that the sum of π and e cannot be equal to a Rational number.

Analyzing Asymmetries with Respect to Rational and Irrational Numbers

It is well understood that 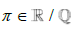[5]. Using the analysis which has already been established, let us consider the difference that exists between the number π and the smallest Rational number greater than π and the largest Rational number less than π. We can write this where for some 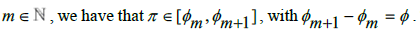Then, from this system of indexing consecutive Rational numbers, where 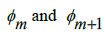are the only Rational numbers in the interval 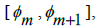, we have that there exists no Integer value that we can multiply by π to acquire a Rational number; since this would allow for to be divided by some Integer to acquire a non-Irrational number in the interval [0, ]. Essentially, since we know that between any two consecutive Rational numbers,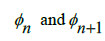, the difference will always be , then in every interval of the form 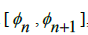there exists at least one unique location between the limits such that we can add or subtract some Rational number to get π. What this allows us to do is to define this unique position of 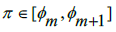in the interval [0,]. We can do this by defining the difference between π and the upper and lower limits of the interval 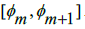This gives us two unique values, 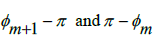both being elements of the interval [0,], where 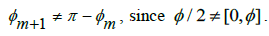Now, since we know that any Irrational number in the interval [0,] will be strictly greater than 0 and strictly less than , if we add any two elements in that interval, we either acquire an Irrational number or . This follows from our indexing for consecutive positive rational numbers; where there exists no Rational numbers between 0 and and from and₂. Then, in the same way that we could subtract π by the first Rational number less than π being _m, to get some number in the interval [0, ], we can do the same for e. 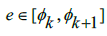Which, since we know that [6],[7],meaning that for some we can write that ;if we then assume that 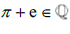we then would need to demonstrate that 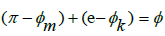must also be true. However, if it can be shown that π and e never correlate by an exact ratio difference, where 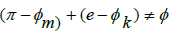and then it is impossible for the two Irrational numbers to sum to a Rational number. Since the fact that π and e are well known to be Irrational numbers and the proofs for this are well accepted, we will not be required to go into the same level of depth which was initially required to prove the fact that π,Instead, we can use the fact that π and e are Irrational numbers and use the following summation series for π formulated by Leibniz et al. and e formulated by Euler to demonstrate that 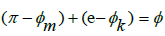, requiring that π+ [8,9] . Where, although there exists other means to demonstrate this proof, the following is offered as it appears to be the most concise argument for demonstration at present. The formulas we will use are as follows, such that,

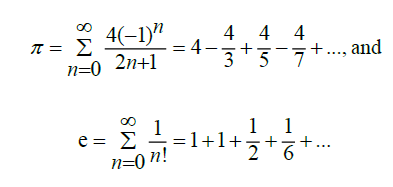
From these series, we can see that the infinite series formula for π alternates between positive and negative terms, summing to π as the number of terms approaches infinity, and that the infinite series formula for e contains only positive terms and similarly sums to e as the number of terms approaches infinity. If we sum the two series, we acquire a formula which approaches the value of π+e as the number of terms goes to infinity. Since we know that individually these formulas approach Irrational number limits, but have yet to determine if when summed together, we get a Rational or Irrational solution, we will need to find some correlation such that π+e can be determined to be Rational or Irrational. Then, whether we take the two formulas and sum them together for each n-designated term, or take the individual components and sum them together based on their consecutive terms from largest to smallest, in both scenarios we end up with the same limit which approaches the value of π+e. We will use the consecutive term method as this will be the most straightforward method to arrive at our conclusion. Let us further simplify our solution by dividing the value π+e by 4. This allows us to remove the 4 value from the numerator in the π formula, while also having no influence over the solution for whether π+e is Rational or Irrational; since dividing a Rational number by a Rational number always gives a Rational solution, and similarly, dividing an Irrational number by a Rational number will always give an Irrational number solution. This allows us to consider the correlation between terms as the series approaches infinity for the individual formulas, and for the series as a whole. We can consider this in the following manner with,

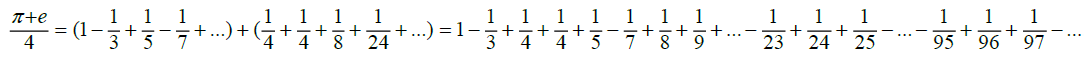
The terms from the e/4 series, when combined with the π/4 series, were made slightly bolder to show where they will add into this long-form version of the expression. What appears to be quite noticeable from this expression is that the consecutive terms for e will consistently increase in distance between the amount of consecutive terms from the π series. Which, having accepted the restriction that if the two Irrational numbers, π and e, sum to a Rational number, then they must be offset by some exact amount for 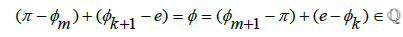to hold true. 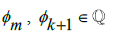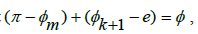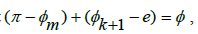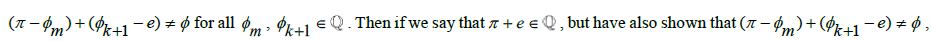Yet, due to the ratio of these terms being offset in a consistently increasing manner between consecutive terms for π and e in the series used, it is impossible for there to exist some such that and since there must exist some then we get a contradiction since for any Rational number, there will always exist some largest Rational number less than it where the difference between both terms will equal, as well as some consecutive smallest Rational number larger than it with the difference also being equal to; which gives us that . . 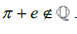Therefore, π+e must be some Irrational number [10].

From this conclusion, following what I hope appears to be a logically self-contained structure of analysis, we now have a simplified means of analyzing Irrational numbers under simple operations of addition and subtraction. The example used demonstrates this aspect, while also requiring that the asymmetry theorem provided be well understood for the subsequent steps to be taken as true. Further, it does not seem logical, or in any way appropriate, to say that this information is enough to determine whether some unique function or limit is an Irrational number. Instead, since every Rational number is equal distance from every consecutive and subsequent Rational number, being defined as a distance of , and there is an Uncountably Infinite number of Irrational numbers between any two Rational numbers, then the difference between every Irrational number and some closest Rational number will always be less than . Meaning that once we know two numbers are Irrational, then we can look for a pattern that either proves or contradicts the argument that the difference between the largest Rational number less than the first Irrational number, and the difference between the largest Rational number less than the second Irrational number, when added together, will sum to a Rational number. If this is impossible, like for the case of π+e, then the solution must equal an Irrational number.

Acknowledgement

I would like to give special thanks to Edward Moylan and Braian Mederos for their insights and critiques during the construction of this paper.

REFERENCES

1. Cantor G. Contributions to the Founding of the Theory of Transfinite Numbers. Dover Publications; 1915.

   [Google Scholar] [Crossref]

2. Cantor G. On a property of the class of all real algebraic numbers. Crelle’s J. Math. 1874;77(1874):258-62.

   [Google Scholar] [Crossref]

3. Boole G.An Investigation of the Laws of Thought: on Which Are Founded the Mathematical Theories of Logic and Probabilities. Kessinger Publ. 2007  [Google Scholar] [Crossref10.2307/2266426]
4. Dickson LE. Richard Dedekind, Essays on the Theory of Numbers: I. Continuity and Irrational Numbers. II. The Nature and Meaning of Numbers.

   [Google Scholar] [Crossref]

5. Niven I. A Simple Proof That π is Irrational. Bull. Am. Math. Soc.1947:53(6);509. [Google Scholar]

   [Crossref]

6. De Stainville J. Blends of algebraic analysis and geometry. Courier; 1815.

   [Google Scholar] [Crossref]

7. Sondow J. A geometric proof that e is irrational and a new measure of its irrationality. Am. Math. Mon. 2006;113(7):637-41.

   [Google Scholar] [Crossref]

8. Leibniz GW. The early mathematical manuscripts of Leibniz, translated from the Latin texts, published by Gerhardt CI, with critical and historical notes by Child JM.

   [Google Scholar] [Crossref]

9. Euler L. Variae observationes circa series infinitas. Comment. acad. sci. imp. Petropolitanae. 1737;9(1737):160-88.

   [Google Scholar] [Crossref]

10. Roy R. The discovery of the series formula for π by Leibniz, Gregory and Nilakantha. Math. mag. 1990;63(5):291-306.

    [Google Scholar] [Crossref]