Research
, Volume: 8( 2) DOI: 10.37532/2320-6756.2020.8(2).189Associated Production and Invariance under Space Inversion
- *Correspondence:
- Spitzer R
Independent Physicist, IME, Berkeley CA 94709-9061, P.O. Box 10061, USA
E-Mail: richard.spitzer@att.net
Received: Jan 7, 2020; Accepted: Feb 3, 2020; Published: Feb 20, 2020
Citation: Spitzer R. Associated Production and Invariance under Space Inversion. J Phys Astron. 2020;8(2):189.
Abstract
A theory is proposed to explain the equality of the domains of validity of associated production and parity conservation in observed hadron processes by their physical identity. The theory accounts for the two phenomena as distinct manifestations of a single symmetry, invariance under space inversion, "P", alone. Its experimental test is provided by processes forbidden by strangeness but allowed by P invariance; specific examples are given. Analysis of already recorded data may reveal their presence. The theory is structured entirely in terms of symmetry-based dynamics-independent concepts, a defining feature of algebraic quantum field theory. It is formulated in terms of a set of localized processes and relations between them that determine the relative phases of P 2 of different hadron states with the same electric charge and baryon number. Observation of the proposed processes will establish associated production to be a consequence of different such relative phase values, without the need for an additional quantum number. Hadron interactions are embodied in the reducible representations of the orthochronous Poincaré group that describe interacting systems. The operation of a fundamental principle is formulated.
Received: Jan 7, 2020; Accepted: Feb 3, 2020; Published: Feb 20, 2020
Citation: Spitzer R. Associated Production and Invariance under Space Inversion. J Phys Astron. 2020;8(2):189.
Keywords
Dynamics independence; Parity superselection; Algebraic quantum field theory; Orthochronous Poincaré group
Abbreviations
AQFT: Algebraic Quantum Field Theory; OPG: Orthochronous Poincaré Group; SO: Set of P2-Compatible Observables
Introduction
Over fifty years ago I proposed that the domains of validity of associated production and parity conservation in observed hadron processes are equal because they are physically identical; i.e. that a single symmetry, invariance under space inversion P alone, explains both sets of phenomena [1].
The currently accepted view involves two unrelated concepts-strangeness and parity-to account for the two phenomena and fails to account for the equality of the two domains. According to this view, the presumed operation of an additively conserved quantum number-strangeness-in all parity-conserving hadron processes render the relative intrinsic parities of hadrons of the same electric charge and baryon number but different strangeness to be indeterminate, that is, a matter of convention rather than of experiment.
The essential view of the theory proposed in this paper is that these relative intrinsic parities are determinate, that is, a matter of experiment rather than of convention, diametrically opposite to the current view. The theory specifies experimentally determinable parities that dictate the defining characteristics of hadron phenomena: (i) associated production, and (ii) its simultaneous breaking with that of invariance under space inversion in purely hadron decays.
I originally implemented the proposed physical identity by a parity-conserving non-minimal electromagnetic coupling of the neutral K meson that determined the relative intrinsic parities of hadrons to be such that P invariance requires their pairwise occurrence [1]. Though this interaction achieved in part its intended goal -reducing the equality of the domains of validity of associated production and parity conservation in hadron processes to their physical identity -it allowed a class of strong processes such as
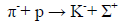 (1)
(1)
in which the new particles K ‾ and Σ+ would appear in pairs but which are not observed.
This shortcoming is remedied in this paper by specifying processes that determine hadron parities to have values that account fully for associated products on the basis of P invariance alone, without introducing an additional quantum number.
The proposed theory is structured entirely in terms of symmetry-based dynamics-independent concepts, a feature that underlies Algebraic Quantum Field Theory (AQFT). The remainder of this section outlines the relations between these concepts and the organization of the paper.
Dynamics independence manifests itself in several distinct roles. It underlies the basic premise of the physical identity of the origins of associated production and P invariance. The theory is formulated in terms of a set of localized observables, a set of parity-conserving hadron processes; locality is likewise a central feature of AQFT. The method of determining relative hadron parities is also dynamics independent, as are the essential consequences of these parities.
The current view regarding associated production is reviewed in Sect. 2. The rationale for the interpretation of the observed equality of the domains of validity of associated production and parity conservation as a manifestation of their physical identity is developed in Sect. 3 on the basis of existing empirical evidence.
The method for determining intrinsic parities by dynamics-independent observables is traced in Sect. 4 to its use in the case of the absolute π0 parity [2]. This method is extended to determine the relative parities of hadrons with the same electric charge and baryon number. These parities are shown in Sect. 5 to divide hadron states into sets distinguished by measurably different values of the phase e2iα of double space inversion P2=e2iα I, where I is the identity operator, I | >=| >; these sets are termed parity-distinct sectors.
The proposed set of processes that determine the hadron parities is specified in Sect. 6. These processes include ones forbidden by strangeness but allowed by a multiplicatively conserved quantum number. They provide the experimental test of the theory. They may be present in already recorded data. Selected such processes are identified. The proposed processes are shown to be consistent with the stability of the Ω -against strong decay.
The fundamental difference between the approach to account for associated production -the absence of specific strong hadron processes that conserve baryons and electric charge -on the basis of parity-distinct sectors and that based on strangeness is shown in Sect. 7 to be tied to the role of measurement in determining the properties of states. Hadron interactions in the dynamics-independent formulation are shown in Sect. 8 to be realized through reducible representations of the orthochronous Poincaré group.
The existence of parity-distinct sectors entails dynamics-independent consequences: two mutually-exclusive symmetry-generated restrictions on possible measurements involving states distinguished by essentially different values of the phase e2iα. These two dynamics-independent restrictions on possible measurements generated by parity-distinct sectors manifest themselves in distinct physical phenomena [3]. These are summarized in Sect. 9, together with their relevance to the interpretation of basic hadron phenomena. One restriction is related to Sect. 10 to associated production; the other, in Sect. 11, to parity violation in purely hadron decays, such as
Σ → N + π (2)
K → 2π (3)
The fact that the proposed physical identity of the origins of associated production and invariance under space inversion is based entirely on dynamics-independent considerations suggests the operation of a fundamental principle. This principle is formulated in Sect. 12.
The theory and its conclusions are summarized in Sect. 13.
Background-Present View as to Associated Production and Related Phenomena
The currently accepted view regarding the strongly-interacting particles discovered more than 60 years ago is reviewed in this section. This provides the empirical background for the proposed theory and identifies the fundamental nature of its point of departure from the current view.
The experimentally determined properties of these particles that originally distinguished them from pions and nucleons were their masses and, in the case of some baryons, also their electric charges. These properties were determined by measurements, such as range-energy relations of tracks in nuclear emulsions, that are independent of any concepts introduced to account for the anomalies in the behavior of these particles in the processes in which they were produced.
This behavior differed from that of pions and nucleons on several counts. (a) Not all processes allowed by electric-charge and baryon conservation were observed. They were produced in pairs from pions and nucleons on very short timescales in processes such as
π + N → K+ + B (4)
where B is a baryon other than a nucleon. (b) Specific kaon-baryon combinations of the pairs, such as (1), and processes in which the new particles appeared singly were not observed; these two aspects of their behavior are collectively referred to as associated production. (c) Their pairwise appearance was broken in their decays, such as (2) and (3), which occur on a vastly longer timescale.
Several assumptions were made to account for this behavior at a phenomenological level. (i) A new quantum number was assumed to be required to account for the observed phenomena. (ii) This quantum number was assumed to be additively conserved in strong processes. (iii) Its values for single-particle states were postulated so as to account for associated production. (iv) To account for decays being inhibited relative to production, this quantum number was assumed not to be conserved in decays. These assumptions were embodied in the strangeness classification scheme, which attributed basic differences to these particles relative to pions and nucleons and assigned values of strangeness S so as to allow the specific electric-charge and kaon-baryon pairs observed in production processes but forbid the unobserved pairs, i.e. to account for (a), (b) and (c); specifically, S=0 to pions and nucleons, and S=+1 to K+ and S=-1 to Σ and K-. Several points should be noted.
First, as to (i), considerations based on invariance under space inversion alone are shown in this paper to account for the observed phenomena without introducing a new quantum number. Observation of those reactions predicted by these considerations that are forbidden by strangeness conservation, e.g. those specified in Sect. 6.1, will render the assumption (ii) of an additively conserved quantum number governing these phenomena to be untenable.
Second, it is important to recognize that the apparent difference in the behavior of nucleons and the other baryon multiplets is no more than an artifact of the status of the nucleon as the lowest-mass baryon multiplet. If the lowest-mass multiplet were any of the others, e.g. the Σ triplet, then the nucleon doublet would have first appeared in pairs in strong interactions such as (Σ,π→N,K), and the norm would have been for the Σ to appear singly in ground-state reactions such as (Σ+,π ‾→Σ0,π0), the counterpart to the actual (p,π‾→n,π0). Such Σ reactions are in fact allowed by strangeness; they have not been investigated in light of the practical difficulty in preparing an initial state comprising two unstable particles. The pairing of the heavier baryon multiplet with the kaon is therefore not a fundamental characteristic for distinguishing it from the nucleon. Rather, the fundamental feature is the appearance of two different kinds of baryons in conjunction with the kaon. However, as shown in Sect. 5, the realization of the physical identity of associated production and invariance under space inversion in hadron processes does render the kaon to differ fundamentally from the pion.
Third, the assignments S=(0,0) and S=(+1,-1) to the pair (K+, Σ-) are both consistent with the processes that do occur. The choice between them is made by requiring S to account for the absence of unobserved processes. This is a separate postulate, not a measurement. As detailed in Sect. 7, it, therefore, differs fundamentally from the proposed method by which the quantum numbers of these particles are determined, which does not invoke such processes.
Fourth, in connection with (c) and (iv), it was believed at the time strangeness was introduced that parity is conserved absolutely. This approach thus assumed two distinct symmetries with two different domains of validity for the conservation of the two attendant quantum numbers: strangeness, an additive quantum number conserved only in strong and electromagnetic processes; and parity, a multiplicative quantum number conserved in all processes. The domain of validity of strangeness conservation was thus presumed to be smaller than that of parity conservation. This is significant in the light of subsequent experimental developments.
A critical piece of additional empirical information was subsequently provided by the discovery of parity violation in decays such as (2), in which strangeness conservation had been taken to be violated from the outset. This result showed that what had originally been thought to be two distinct domains of validity coincided exactly. The observed domain of validity of invariance under space inversion in hadron processes was reduced to that of the previously assumed domain of validity of strangeness conservation. Yet, the two constructs are distinct and conceptually unrelated. The equality of their domains of validity remains an unaccounted-for empirical fact within the present view.
The issues then became to account not only for (I) the fact that not all strong processes allowed by electric-charge and baryon conservation were observed but also for (II) the simultaneous breaking of associated production and parity conservation in decays of these particles.
The exact empirical coincidence of these two domains presents a puzzle, in that their operational definitions are very different. The resolution of this puzzle I originally proposed [1] is summarized in the next section.
Physical Identity of Origins of Associated Production and Parity Conservation
The puzzle presented by the empirical equality of the domains of validity of associated production and parity conservation in strong processes, as manifested by the simultaneous breaking of the two domains in hadron decays, is directly analogous to that found in the numerical equality of inertial and gravitational mass in Newtonian gravity: two distinct operational definitions of physical properties that behave empirically as one. The resolution of this puzzle in gravity is embodied in the equivalence principle, according to which the two masses are equal because they are physically identical.
In my view, the case for explaining the equality of the domains of validity of associated production and parity conservation in the strong process as a manifestation of their physical identity is as compelling as that for explaining the numerical equality of inertial and gravitational mass within Newtonian gravity in terms of their physical identity. The analogy between the empirical puzzle in strong processes and that in Newtonian gravity is extended in this paper to its resolution: the domains of validity of associated production and parity conservation in strong processes are equal because they are physically identical [1]. The equality of the two domains is accounted for by the operation of a single symmetry: invariance under space inversion.
To realize this physical identity, the intrinsic parities must be determined experimentally to have values such that the unobserved processes are forbidden on the basis of these values alone, without introducing an additional quantum number.
Background on Intrinsic Parities
The conventional method of determining intrinsic parities theoretically is to specify interactions that are invariant under space inversion P only for the specifically determined values. This method can account fully for associated production on the basis of invariance under space inversion alone, i.e. without introducing an additional quantum number. However, the relevant interactions also predict a strong process at variance with existing data.
An alternative method for determining intrinsic parities is to specify a set of observables. This method, though less familiar than the conventional one, is more fundamental, as it is dynamics independent. It was advanced 70 years ago to determine the π0 parity from the correlation between the polarization of the two photons in π0 decay [2]. Because of the difficulty presented by the measurement of this correlation, the π0 parity,
η(π0)= –1 (5)
was actually determined experimentally by a dynamics-dependent analysis of a process in which the decay photons are internally converted [4].
The history of the determination of the π0 parity highlights the importance of distinguishing between the conceptual framework for dynamics-independent parity determination and the practical considerations of determining these parities experimentally. This distinction is even more significant for the analysis in Sect. 5 of the general determination of relative parities of hadrons with the same electric charge and baryon number than it is in the case of the π0.
The dynamics-independent method avoids the conflict with existing data in explaining associated production by intrinsic parity alone that seems inherent to the dynamics-dependent method.
Because of existing empirical restrictions on the measurability of Hermitian operators connecting hadrons of different electric charge or baryon number (empirical electric-charge and baryon superselection), the intrinsic parity of a hadron is physically meaningful only relative to that of another hadron of the same electric charge and baryon number.
To my knowledge, the question of distinguishing intrinsic parities of spin-½ particles experimentally was first posed by Fermi at a conference in which he organized a separate session devoted to the intrinsic parities of spin-½ fields [5]. Fermi also raised the issue of arbitrariness in the parity of a spin-½ particle: "eiα, α real but arbitrary". Wigner posited that "This would be perfectly permissible... but would have no physical significance."
According to Wightman [6], the discussion initiated by Fermi was the trigger for the original paper on superselection [7]. The prevailing view at present is that the absolute intrinsic parity of a spin-½ particle, as well as the relative parity of particles with different electric charge, baryon number, or strangeness is a matter of convention.
My view differs essentially from the prevailing one in that the proposed physical identity of the origins of associated production and parity conservation is based on the proposition that the relative parities of any two hadron states with the same electric charge and baryon number, and presently considered to be distinguished by different strangeness, are measurable.
The restriction on measuring the absolute intrinsic parity of a charged-meson or any baryon state is expressed by the statement that the phase e2iα of P2, e.g.
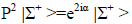 (6)
(6)
is a matter of convention; i.e. it can be removed by a permissible phase change for any individual baryon or electrically-charged meson.
However, experimental confirmation of the strangeness-forbidden processes proposed in Sect. 5 would establish the relative intrinsic parity η of two such states to be determinate; e.g.

i.e. this relative phase is then not a matter of convention and cannot be removed.
The relative parities of hadrons with the same electric charge and baryon number would then not only be established to be physically meaningful, but the assumption that an additively conserved quantum number governs strong processes would thereby be rendered to be untenable.
Parity-Distinct Hadron Sectors
The realization of the physical identity I proposed [1] for the origins of associated production and parity conservation in hadron processes is rooted in two distinct aspects of invariance under double space inversion P2: determining the relative P2 values of hadron states with the same electric charge and baryon number by a set of localized observables, and the consequences of these values. Both are independent of the dynamical structure of the system.
A formulation of particle interactions in terms of a set of localized observables and the relations among them is the basis for Algebraic Quantum Field Theory (AQFT) [8]. In this approach, algebraic relations between observables take on the primary role played by Hamiltonian-generated equations of motion in the conventional formulation of QFT.
The particle interactions that result in the proposed physical identity are formulated in terms of a set of processes and their relations. The basic processes that anchor relative hadron parities are specified in Sect. 5.2 The set of processes that determine the relative values of P2 of hadrons with the same electric charge and baryon number is specified in Sect. 5.3. I assume that a single algebra of observables underlies this set of processes.
Various consequences of these essentially different values of P2 and their significance for observable hadron processes are examined in Sects. 9-11.
Sectors generated by double space inversion
Central to the formulation of the proposed physical identity in hadron phenomena is the concept of sectors: sets of states distinguished by essentially different values of the phase of operators in the Hilbert space H of these states that are phase multiples of the identity [7].
5.1.1 Parity-distinct sectors: Dynamics-independent P2 invariance is imposed in this section directly on a set of processes to determine the relative parities of physically-distinct hadron states with the same electric charge and baryon number. Results for individual processes are combined and shown to split the space H of these hadron states into sectors distinguished by measurably different relative values of phase e2iα of P2=e2iα I. These will be termed to be parity distinct. Hadron states whose relative parity is a matter of convention according to strangeness, e.g. |n> and |Σ0>, are accordingly characterized operationally by essentially different values of e2iα.
Parity-distinct sectors divide the set A of Hermitian operators in H into two mutually-exclusive subsets: operators with nonvanishing matrix elements connecting only states with the same value of P2 (subset A1), and the complementary subset A2=A - A1, with nonvanishing matrix elements connecting only parity-distinct sectors. Sectors containing only the elements A1 will be termed to be parity coherent. Measurement of elements of A1 will be termed to be compatible with invariance under space inversion. Elements of A2 will be termed potential observables, as these elements have not been observed in all symmetries that generate distinct sectors. Measurement of an element of A2 converts a potential observable into an actual observable [3].
Collectively, parity-distinct sectors, the specific relative values of P2 for these sectors, and the consequences of the relations between the products of these values play decisive roles in the formulation of the proposed theory.
5.1.2 Relative sector parity: It is convenient to define the parity signature of two states |a> and |b> with the same baryon number and electric charge as the ratio of the squares of their intrinsic parities,
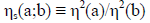 (8a)
(8a)
Its generalization to multiparticle states is, e.g.
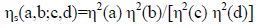 (8b)
(8b)
For states with the same value of e2iα, the parity signature is unity,
ηs(a;b)=+1 (8c)
Processes compatible with P invariance can connect only states with the same value of e2iα.
For states in parity-distinct sectors, the parity signature
ηs(a;b) ≠ +1 (9)
will be referred to as the relative sector parity.
Parities of neutral mesons
Dynamics-independent determination of hadron parities is anchored in that of neutral mesons. The latter follow in principle from dynamics-independent considerations of the known π0 decay and two postulated processes:

where N is a nucleon. The processes (11) are forbidden by an additively-conserved quantum number.
The π0 parity is given by (Eqn. 5). The K0 and 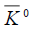 parities follow from a consideration of the relative orbital parities (li,lf) of the initial and final states in (Eqn. 11). The orbital parity of the four kaons in the final states in (Eqn. 11) must be even, as the wave function of any two of them has to be symmetric in their interchange. Hence, the product of the K0 parities is given as
parities follow from a consideration of the relative orbital parities (li,lf) of the initial and final states in (Eqn. 11). The orbital parity of the four kaons in the final states in (Eqn. 11) must be even, as the wave function of any two of them has to be symmetric in their interchange. Hence, the product of the K0 parities is given as
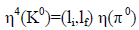 (12)
(12)
with 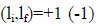 according to as the orbital parity of the π0 relative to that of the nucleon is the same as (opposite to) the relative orbital parity of the four kaons to the nucleon.
according to as the orbital parity of the π0 relative to that of the nucleon is the same as (opposite to) the relative orbital parity of the four kaons to the nucleon.
The solutions of (12) are
 (13a)
(13a)
and
 (13b)
(13b)
The solution (Eqn. 13b), for which (li,lf)=-1, comprises two subsets of observables, one of which is subject to parity superselection while the other is not. The set SO of parity-conserving processes linked to this solution cannot, therefore, be characterized by a single algebra of observables. This solution will not be considered further.
The set SO of observables can be characterized by a single algebra of observables for the solution (Eqn. 13a), as the entire set is subject to unique parity superselection. This solution entails that (li,lf) must be positive, which can be tested in principle. Determination of kaon parities by processes (Eqn. 11) is likely to be difficult, but this has no bearing on their theoretical role. As detailed in Sect. 4, practical difficulties in the dynamics-independent determination of the π0 parity led to its determination by a dynamics-dependent analysis of a related process. Similarly, the kaon parity may be determined more readily by the processes

upon the use of the relation

which is itself obtained by a dynamics-dependent analysis [9].
The 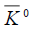 parity follows most directly from the relation
parity follows most directly from the relation
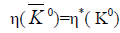 (16)
(16)
It is convenient to introduce the notation

for the neutral-K parities.
Hadron-sector parities
The properties of single-baryon states of a given electric charge are developed on the basis of dynamics-independent considerations of P2 invariance. This operation splits the Hilbert space of hadron states with the same electric charge and baryon number into parity-distinct sectors, sectors distinguished by measurably different relative values of P2.
The structure of the parity-distinct sectors depends essentially on the experimentally realized scope of the particle spectrum I introduced in my original proposal for the physical identity of the origins of associated production and P invariance. This spectrum included two new particles, 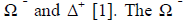 was subsequently proposed by others and was eventually observed. I defined the Δ+ operationally by the reaction p + p → Σ+ + Δ+. Since then, the label "Δ+ " has been applied otherwise, so I will hereafter refer to this particle as "A + " rather than as "Δ+ ".
was subsequently proposed by others and was eventually observed. I defined the Δ+ operationally by the reaction p + p → Σ+ + Δ+. Since then, the label "Δ+ " has been applied otherwise, so I will hereafter refer to this particle as "A + " rather than as "Δ+ ".
The A + would be produced in processes such as

Existence of such a particle is in itself consistent with an additively-conserved quantum number. To my knowledge, it has not been observed to date.
5.3.1 A set of single-baryon hadron states: There are four physically different single-baryon states BQj for each of three electric charges Q=(+1,0,-1) and sector number j in the baryon set without the A+, five in the set with the A+. The baryons in different sectors SQj are distinguished empirically by their mass and by different electric-charge structures. A more consequential difference, in terms of relative baryon parities, is considered in Sect. 5.3.2.
Some of the states also include one or two charged pions, to enable characterization of all baryon multiplets by their relative parities for all three charges. A complete set of such hadron states is shown in TABLE 1 for the three values of Q and all values of j.
| BQj | |||
|---|---|---|---|
| ↓SQj↓ | B1j | B0j | B-1j |
| SQ0 | A+ | π –, A + | 2π –, A+ |
| SQ1 | p | n | π–, n |
| SQ2 | Σ+ | Σ0, Λ0 | Σ ‾ |
| SQ3 | π+, Ξ0 | Ξ0 | Ξ ‾ |
| SQ4 | 2 π+, Ω ‾ | π+, Ω ‾ | Ω ‾ |
TABLE 1. A set of single-baryon states BQj for three electric charges Q and five sectors SQj.
The structure of this set is invariant under a concurrent single-particle interchange of baryons between the two singlets, between the two doublets, and within the triplet; and of pions:
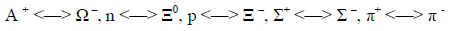
Corresponding results obtain for other hadron states with the same baryon number and electric charge.
5.3.2 Relative parities of selected hadron sectors: The relative sector parities of charged mesons and of the set of single-baryon states in TABLE 1 follow from those for the neutral mesons and known processes, for which ηs=1, by multiplying sector parities, i.e. by using relations such as
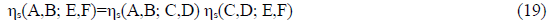
For example, using
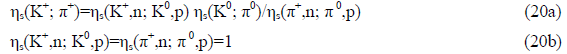
one gets

for the relative K+- π+ sector parity.
Similarly, we get,

Dynamics-independent analysis of the single-baryon hadron states BQj thus shows that the physically different states with a given electric charge are characterized by specific relative parities. The relative sector parities for this set of single-baryon hadron states are shown in TABLE 2. Consecutively numbered sectors have relative parity
| without A+ | with A+ | ||
|---|---|---|---|
| ↓SQj↓ | BQj | ηs(BQ1; BQj) | ηs(BQ0; BQj) |
| SQ0 | A | – | 1 |
| SQ1 | N | 1 | ω |
| SQ2 | Σ, Λ | ω | ω2 |
| SQ3 | Ξ | ω2 | ω3 |
| SQ4 | Ω | ω3 | 1 |
TABLE 2. Relative sector parities, ηs(BQj; BQj+1)=ω, for a self-contained set of single-baryon parity-distinct sectors.

These spin-½ particles with different parities can be distinguished experimentally by the processes that determine their relative parities because they have different masses.
The entry for (with A+, SQ4) follows from the relation ω4=+1. Though there are five physically different sectors SQj, j=0-4, for the set of observables that includes the A+, the sectors defined by the A+ and Ω‾, suitably adjusted for an electric charge (TABLE 1), are parity coherent. Pairs of parity-distinct sectors with relative parity ω will be termed neighboring sectors. Determination of these relative sector parities would confirm the notion that the domains of validity of associated production and parity conservation are equal because they are physically identical.
5.3.3 Structure of the single-baryon sectors: The presence of the A+ in the particle spectrum affects fundamentally the structure of the parity-distinct sectors. It is linear without the A+. In the presence of the A+, the relative sector parities for the single-baryon sectors form a cyclic group of order 4.
6. The Set of Observables
The set of P2 -compatible observables (SO) is derived, by dynamics-independent considerations, from those processes compatible with an additively-conserved quantum number and the postulated processes that are incompatible with its conservation.
6.1 Elements of SO
Elements of the SO are taken to comprise those of three subsets: (i) the subset SO1 of strong processes that are allowed by an additively-conserved quantum number; (ii) the subset SO2 of processes (10) and (11a,b) that determine neutral-meson parities; and (iii) the subset SO3 comprising elements corresponding to the parity signatures generated by multiplication of parity signatures of elements of SO1 and SO2, Eq. (19) and its generalizations. In the case of decays, the elements of SO are additionally constrained by energy conservation.
The set of observables is thus "additive", in the sense that if the processes
A + B → C + D (23a)
C + D → E + F (23b)
are allowed, then so is the process
A + B → E + F (23c)
The processes that determine the neutral-K parities and those in the entire subset SO3, none of which has as yet been observed to my knowledge, are at variance with the assumption that an additively-conserved quantum number governs strong hadron processes.
The SO is a more restrictive set than the one defined by all transitions between parity-coherent sectors; i.e. there are elements in the latter that are absent from the SO. The condition that the parity signature of initial and final states of any process compatible with P2 invariance be unity is thus necessary but not sufficient for this process to be an element of the SO; e.g. the following four processes satisfy this condition, but none is an element of the SO:

Elements of SO3 include processes such as

where the energy of the two photons in (25f) is equal to the π0 mass and that of the photon in (25g) is equal to the (Σ0,Λ0) mass difference. Possible parity-signature relations corresponding to these processes are given in the Appendix. Some of these processes may already have been recorded in existing experimental data, but were missed because processes with the same initial states were studied in other contexts. Analysis of recorded data may reveal their presence. Their observation would render the presently held view that strong hadron processes are governed by an additively conserved quantum number to be untenable.
6.2 Ω- stability
The strong decay

which would occur on a much shorter time scale than the observed Ω- lifetime, is allowed energetically but has not been observed. Its initial and final states belong to a parity-coherent sector,

Though this decay is allowed on the basis of dynamics-independent P2 invariance, it is not an element of SO, in conformance with its empirical absence as a strong process.
The related decay

where the energy of the two photons is equal to the π0 mass, is an element of SO but is energetically forbidden.
6.3 A+ mass
If the A+ exists, the initial and final states in the parity-conserving decay

would belong to a parity-coherent sector, but this decay is not an element of SO. The related decay

where the energy of the two photons is equal to the π0 mass, is an element of SO. Ω -stability against this decay requires the A+ mass to be larger than 1253 MeV.
Likewise, the parity-conserving decay

where the energy of the two photons is equal to the π0 mass, is an element of the set SO. If the A+ is to be stable against this decay, its mass would have to be smaller than 2091 MeV. If this condition is not satisfied, the A+ would be replaced in processes such as (18), (25d,e) by the final state in (30).
7. Measurement in Hadron Processes
Two aspects of the fundamental role of measurement in quantum mechanics provide the theoretical framework for my interpretation of basic hadron phenomena. One, considered in this section, is its role in determining the measurably different values of phase e2iα of P2. The other, its role in the dynamics-independent restrictions on possible measurements consequent to the measurably different values of e2iα, is considered in Sects. 9-11. Both bear on the essential difference between my approach and that of strangeness to account for associated production.
7.1 Determination of properties of states-measurement versus postulate
The common goal of the two approaches to explain associated production-the one based on parity-distinct sectors and the one based on strangeness -is to account for the absence of unobserved two-particle channels. Specifically, the new particles in the observed channels are presumed to differ from pions and nucleons, in addition to their different masses and electric charges, by some internal degree of freedom whose values for the initial and final states in unobserved channels are unequal. The values of intrinsic parities that predict the absence of these processes are determinable by measurement. Parity-conserving processes-those already observed and those that serve as a test of the proposed theory but are as yet unconfirmed-determine relative values of P2 uniquely so as to exclude the unobserved processes. The absence of specific channels is thus explained on the basis of the properties of the states in the observed channels alone.
In contrast, strangeness-conserving processes do not distinguish between those assignments of strangeness that do account for this absence and the ones that do not. The choice of values of strangeness is a separate postulate, made by invoking the absence of unobserved channels. The role of measurement is critical to the difference between the two approaches. The methodologies used in the two approaches thus differ fundamentally.
I adhere to the generally accepted view of "measurement" in quantum mechanics to mean determining the value of a physical observable of a quantum object by its interaction with a macroscopic measuring apparatus. I treat quantum observation in the spirit of the operational viewpoint advocated over the years for atomic physics by Lamb [10]. As adapted to hadron processes, this comprises (i) initial-state preparation; (ii) an event localized in a small spacetime region, e.g. a collision process such as (4) or a decay such as (2), to produce a variety of output channels; and (iii) final-state analysis in terms of an experimental procedure described operationally, i.e. in physical terms.
The measurement process is generally considered to be completed when its outcome has been observed, i.e. information about the value of some initial-system observable has been transferred, via a macroscopic variable of the measuring apparatus, to the observer. Measurement on a single channel analyzed in isolation is complete when the physical observables relevant to that lone channel have been operationally defined.
In the case of associated production, the analysis of the final state -and therefore the goal of the measurement -is broadened from consideration of the properties of the particles in a single channel to relating their internal properties in multiple channels. The measurement can then be regarded as having been completed only when this internal degree of freedom is itself determined operationally.
The two methodologies are identical through the first two stages of measurement and the first part of the third stage. Whatever idealizations are made in the following discussion of these stages of the measurement process, they are common to the two approaches (Sect. 7.2). The focus here is on the differences between the methodology based on parity-distinct sectors (Sect. 7.3) and that based on strangeness (Sect. 7.4). This difference comes into play in the last part of the final-state analysis, in which the internal degrees of freedom of the individual particles are to be determined so as to account for the absence of the unobserved channels. The differences between the two approaches are summarized in Sect. 7.5.
7.2 Methodology common to the two approaches
The following discussion of the part of the measurement process common to the two approaches is confined to the concepts needed for establishing the differences between them. (The fact that measurements are made on an ensemble of similarly prepared systems rather than on a single system is also disregarded, as this aspect is common to the two approaches.)
After the interaction of the collision-produced quantum system with the measurement apparatus, the density matrix for a single channel of the coupled system is effectively reduced to diagonal form. In the following analysis, this single-channel state is described by a wave function Ψ expressed as a direct product of the wave functions of the components of the coupled system,
 (31)
(31)
where (χi,ζi) represents a state of the particles produced in the collision, (φi, ξi) represents the corresponding state of the measuring apparatus, ζi and ξi represent the respective internal degrees of freedom, |αi|2 is the probability of the state χi, and  denotes a direct product.
denotes a direct product.
The two particles produced in the collision are identified operationally as being different from those in the initially prepared state by having considered the state of the measuring apparatus, e.g. tracks in a bubble chamber; application of known conservation laws; and correlation between the state of the apparatus and that of the microscopic system produced by the collision, as given by (Eqn. 31). Analysis of the results for each single channel establishes the production of particles that differ operationally from pions and nucleons by their masses and electric charges.
Consideration of other possible two-particle channels shows that not all channels allowed by the conservation of electric charge and baryon number are present in the final state. At this stage of the measurement, both approaches assume the existence of an internal degree of freedom that is to account for the absence of the unobserved processes. The two methodologies are identical through this stage of the final-state analysis.
After this internal degree of freedom has been identified, the remaining measurement issue is to determine its values for individual particles so as to account operationally for those two-particle output channels that would conserve electric charge and baryons but are not observed.
As shown next, the methodology based on parity-distinct sectors differs fundamentally from that of strangeness not only in the nature of this internal degree of freedom (multiplicative vs additive quantum number) but also in the method by which its values are established: measurement versus postulate.
7.3 Methodology based on parity-distinct sectors
Determining these internal system properties-relative sector parities-completes the final-state analysis of the measurement process extended to include multiple channels. Measurements made on observed processes alone, which are compatible with invariance under space inversion, determine these sector parities of the multichannel states so as to exclude the unobserved channels from this set of processes. This conforms to the general principle of quantum mechanics that requires properties of states to be determined by measurement.
Conventionally, the measurement process is described in terms of a Hamiltonian, typically enlarged from that for the first two stages of the measurement process to include some portion of the measuring apparatus. In the case of associated production, this holds for those stages of the measurement process that are common to the two approaches. Within the approach based on parity, the last stage of the final-state analysis does not require further enlarging of the dynamical system; parity-distinct sectors -a dynamics-independent concept -dictates the results.
For example, the projection operator for a process such as (1) is

where wmn is an element of the corresponding density matrix. According to (21a), (21d), (17a) and (13a), the relative sector parity of the states 

The transformation of this operator under P2 is accordingly given as
 (34)
(34)
Transitions between states in these unobserved processes are thus theoretically incompatible with invariance under space inversion as a consequence of dynamics-independent considerations. Such processes are thus theoretically excluded from the subset of observables compatible with invariance under space inversion.
7.4 Methodology based on the strangeness
The methodology of a classification scheme such as strangeness differs fundamentally from that based on parity-distinct sectors. The symmetry constraint imposed by strangeness conservation on a process such as
a + b → c + d (35a)
is
S(a) + S(b)=S(c) + S(d) (35b)
where the values S of strangeness are assumed to be integers.
The values of S assigned on the basis of an observed process, e.g. to the particles in (4),
S(π)=0, S(N)=0, S(K+)=+1, S(B )=–1 (36a)
are selected so as to satisfy (35b) and to violate this condition for unobserved processes such as (1). However, observed processes such as (4) are also consistent with the assignment
S(π)=0, S(N)=0, S(K+)=0, S(B)=0 (36b)
which does not account for the absence of the unobserved processes. The choice of (36a) is not a measurement but a separate postulate, made expressly to account for unobserved processes.
Unlike the procedure based on measured parities, which explains associated production on the basis of observed processes alone, strangeness assignment makes essential use of unobserved processes.
7.5 Summary of differences
The differences between the methodology based on intrinsic parity and that based on strangeness to determine the internal degree of freedom that accounts for associated production are summarized in TABLE 3.
| Intrinsic parity, η | Strangeness, S | |
|---|---|---|
| Type of quantum number | multiplicative | additive |
| General constraint | |η|=1, imposed by quantum field theory | S=0, ± 1, - 2, ... assumed |
| Invariance-imposed constraint by process a+b → c+d | η2(a) η2(b)=η2(c) η2(d), i.e. ηs(a, b; c, d)=1 | S(a)+S(b)=S(c)+S(d) |
| Relative intrinsic parity of hadrons with same electric charge and baryon number | physically meaningful | physically meaningless for hadrons with different values of S |
| Value of a quantum number | absolute for neutral mesons; relative for baryons and charged mesons* | absolute for every particle |
| Invokes absence of unobserved processes to assign a quantum number | no | yes |
| Method of assigning quantum numbers to account for the absence of unobserved processes | determined by measurement; absence is a consequence of values of η2 determined experimentally | absence is used explicitly as input; a new quantum number is introduced; its values are assigned by separate postulate so as to account for the absence |
| Equality of domains of validity of associated production and parity conservation | the two domains are equal because they are physically identical; no need for a new quantum number | the two domains are unrelated conceptually; their equality remains unaccounted for |
*consequence of the empirical fact that a coherent superposition of states with different electric charges or different baryon numbers has never been prepared
TABLE 3. Comparison of the two methodologies.
8. Particle Interaction and Reducible Representations of the Orthochronous Poincaré Group
Superselection engenders a novel feature if parity is included in the classification of internal hadron properties.
The irreducible representations of the restricted (proper orthochronous) Poincaré group classify a single particle in terms of its mass and spin. The intrinsic parity of baryons and electrically-charged mesons is on a different footing than that of their mass or spin because of univalent (spin) and empirical electric-charge superselection. Specifically, neutral mesons apart, intrinsic parity has no physical significance in the isolated behavior of anyone hadron by itself; it manifests itself only in the interaction of two or more of them. Interacting systems transform, in general, according to reducible representations of the Poincaré group. Physically meaningful classification of internal properties of baryons and charged mesons by representations of the restricted Poincaré group extended to include space inversion (orthochronous Poincaré group, OPG) thus necessarily involves its reducible representations.
In order for a process to be compatible with invariance under space inversion, it must connect elements of parity-coherent sectors; i.e. the relative sector parity of the initial and final states in such processes must be +1. Processes that connect parity-distinct sectors are excluded from the subset of observables compatible with P invariance. This section delineates selected pairs of interacting two-particle single-baryon states that serve as the representation space for those reducible representations of the OPG that describe interacting hadrons in two-particle processes connecting parity-coherent sectors in this space and characterize its structure.
8.1 Relative sector parities for two-hadron processes
Single-baryon states from different multiplets were shown in Sect 5.3 to belong to parity-distinct sectors, as do single-particle pion and kaon states. These two sets of single-particle states in parity-distinct sectors can nonetheless be combined to form two-particle states with the same electric charge Q that belongs to parity-coherent sectors, albeit only for specific combinations of initial and final states. The set of P-invariant hadron processes is thereby restricted to a smaller subset than that allowed by the conservation of electric charge and baryon number alone.
The parity signatures of a selected set of single-baryon two-hadron states with Q=0 are shown in TABLE 4. These signatures divide into two subsets: (i) those for states within parity-coherent sectors, for which ηs(a, b, c, d)=+1; and (ii) those for states in parity-distinct sectors. Entries for  are identical to those for (π–, p), (π–, Σ+), (K–, p), (K+, Σ–), (K–, Σ+), respectively, and have been suppressed. This reflects the parity coherence of sectors related by charge independence.
are identical to those for (π–, p), (π–, Σ+), (K–, p), (K+, Σ–), (K–, Σ+), respectively, and have been suppressed. This reflects the parity coherence of sectors related by charge independence.
| a,b | ||||||
|---|---|---|---|---|---|---|
| ↓ c, d ↓ | π–, p | π–, Σ+ | K–, p | K0, n | K+, Σ– | K–, Σ+ |
| π–, p | 1 | ω* | ω* | ω | 1 | -1 |
| π–, Σ+ | ω | 1 | 1 | -1 | ω | ω* |
| K–, p | ω | 1 | 1 | -1 | ω | ω* |
| K0, n | ω* | -1 | -1 | 1 | ω* | - ω* |
| K+, Σ– | 1 | ω* | ω* | ω | 1 | -1 |
| K–, Σ+ | -1 | ω | ω | - ω | -1 | 1 |
TABLE 4. Parity signature of the state |a, b> relative to the state |c, d>: ηs (a, b; c, d)=η2(a)η2(b)/[η2(c)η2(d)].
The relative sector parities ηs (p;Σ+)=ω and ηs (K‾;π–)=ω* are seen to compensate each other exactly, so as to place the states |p, K‾ > and |Σ+, π-> in a parity-coherent sector:
 (37)
(37)
This result is foregone, as relative sector parities were determined by imposing P2 invariance on observable processes. The essential point is that all processes between the two-particle states in TABLE 4 that connect parity-coherent sectors correspond to parity-conserving processes that have been observed, and all processes between the states in TABLE 4 that connect parity-distinct sectors are known empirically to be absent from parity-conserving processes.
Thiegone, as relative sector parities were determined by imposing P2 invariance on observable processes. The essential point is that all processes between the two-particle states in TABLE 4 that connect parity-coherent sectors correspond to parity-conserving processes that have been observed, and all processes between the states in TABLE 4 that connect parity-distinct sectors are known empirically to be absent from parity-conserving processes.
The relative parities of the parity-distinct sectors in TABLE 4 are ω, a complex number of modulus unity, and -1. These values correspond to two distinct kinds of unobserved strong processes: those in which hadrons other than pions and nucleons would occur singly, such as
π-+ p → π-+ Σ+ (38)
for which
ηs (π–,p; π–,Σ+)=ω (39)
and those in which they would be paired but the reactions are nonetheless not observed, such as (1), for which
ηs (π–,p; K–,Σ+)=-1 (40)
8.2 Reducible representations of the orthochronous Poincaré group
The following discussion involves the Hilbert space of states, elements of the orthochronous Poincaré group and operators representing them, and the parity-distinct sectors that generate parity superselection.
In general, multihadron states transform according to reducible representations of the Poincaré group [11]. Noninteracting multihadron states transform as direct products of the single-hadron states; their relative intrinsic parities are in general unspecified. The operators representing the transformation of the Poincaré group for noninteracting states are direct products of the operators representing the separate systems; most simply, in terms of irreducible representations.
Hadron interactions are described in the dynamics-independent formulation by operators representing reducible representations of the Poincaré group that cannot be decomposed into operators for the noninteracting system. The importance of examining reducible representations of the Poincaré group in the context of studying interacting relativistic systems was emphasized more than fifty years ago by Dirac: "All the work that has been done on quantum field theory may be looked upon as an attempt to set up a suitable (reducible) representation of the inhomogeneous Lorentz group corresponding to physical reality" [12].
The states in TABLE 4 form the basis for describing the two-hadron baryon-meson interaction. The interaction determines parity-distinct sectors -sets of states distinguished by measurably different values of phase e2iα of P2. It thereby changes the properties of the noninteracting multihadron system in several respects.
The structure of Hilbert space changes from one already divided into distinct sectors by the univalent, baryon, and electric-charge superselections imposed on the noninteracting multihadron system into one divided additionally into the interaction-generated parity-distinct sectors in the case of the interacting system. This restricts the attendant set of P-invariant observables to the subset of processes that connect parity-coherent sectors, a smaller set than the one allowed by the noninteracting superselection structure. These processes realize dynamics independence of the localized hadron interactions that generate associated production. The interaction enlarges the symmetry group from the restricted Poincaré group in the case of the noninteracting system to the orthochronous Poincaré group (OPG) in the case of the interacting system. It changes the nature of the transformation properties of the multihadron states from those based on direct products of irreducible representations in the case of the noninteracting system into ones based on reducible representations in the case of the interacting system.
The effect of interaction must be embodied in the changed structure of the operators representing the transformations of the Poincaré group. 1) These operators change from direct products of those representing elements of the restricted group for the noninteracting system to operators representing elements of the orthochronous group for the interacting system; the latter cannot be decomposed into operators for the noninteracting system. 2) The operators for the interacting systems act in a multisector Hilbert space comprising parity-distinct sectors that generate parity superselection. Their structure must reflect the exclusion from the set of processes compatible with the OPG of processes connecting states with essentially different values of e2iα. 3) Each set of two-hadron states within a coherent subspace serves as a Hilbert space for the representations of the OPG that characterize the interactions that generate this set. The structure of the sets of these operators in each of the parity-coherent subspaces is determined by the sets of processes connecting the states in these subspaces and the charge structures of the baryon multiplets. 4) The structure of these operators must incorporate invariance of the structure of the set of single-baryon states under a concurrent interchange of baryons among multiplets with the same number of baryons. 5) These operators incorporate the function of the kaon as the carrier of intrinsic parity between parity-distinct baryon multiplets.
9. Restrictions on Possible Measurements
Dynamics-independent considerations of the SO processes determine sets of states distinguished by essentially different values of the phase of P2 (parity-distinct sectors). These sectors, in turn, result in dynamics-independent restrictions on possible measurements. The relevance of these restrictions to the interpretation of basic hadron phenomena is grounded in concepts developed in the preceding paper [3].
The restriction on possible measurements generated by parity-distinct sectors is unconditional: the incompatibility of the operation of P invariance and the measurability of processes connecting such sectors. This is a purely theoretical restriction, invariably operative upon determination of parity-distinct sectors.
This unconditional restriction engenders two mutually-exclusive conditions on possible observables: (a) limitation to those processes compatible with P2 invariance, and (b) limitation to those processes connecting parity-distinct sectors.
These two conditions result in two distinct, mutually-exclusive, dynamics-independent conditional restrictions on possible measurements: (i) exclusion from the subset of observables compatible with P2 invariance of processes connecting parity-distinct sectors (superselection on parity), and (ii) breaking of space-inversion symmetry by processes connecting such sectors. These restrictions are summarized in TABLE 5.
| Unconditional restriction on possible measurements | Mutually exclusive conditional restrictions exclusion symmetry breaking |
|
|---|---|---|
| incompatibility of operation of P invariance and measurability of processes connecting parity-distinct sectors | condition: observables limited to those compatible with P invariance; consequence: exclusion of processes connecting parity-distinct sectors from such observables -parity superselection |
condition: observables limited to processes connecting parity-distinct sectors; consequence: the measurement-generated breaking of P invariance |
TABLE 5. Dynamics-independent conditional restrictions on possible measurements: parity superselection and measurement-generated symmetry breaking.
The conditional restrictions have both theoretical and empirical contexts [3]. It is essential to distinguish between these two contexts.
The incompatibility of the measurement of processes connecting parity-distinct sectors and invariance under space inversion thus has two distinct physical consequences; these are dictated by the imposed conditions. Associated production as a manifestation of parity superselection is addressed in Sect. 10. The complementary aspect, dynamics-independent breaking of P invariance in pure hadron decays, is addressed in Sect. 11.
10. Associated Production as Parity Superselection
Parity superselection excludes processes connecting the specific combinations of initial and final states distinguished by different values of the phase of P2 from the subset of two-hadron processes compatible with P2 invariance.
Dynamics-independent theoretical considerations based on relative sector parities determinable by the SO thus restrict P-invariant processes to the specific subset of those allowed by charge and baryon conservation that connect parity-coherent sectors.
The empirical phenomenon of associated production manifests itself in the absence of selected two-hadron processes that would be compatible with electric-charge and baryon conservation.
As shown in Sect. 8.1, the subset of two-hadron processes allowed theoretically by parity superselection coincides exactly with the specific pairwise combinations observed in associated production. The subset excluded by the theoretical context of parity superselection coincides exactly with the subset known empirically to be absent. Experimental confirmation of the proposed processes that violate strangeness would thereby establish that the empirical phenomenon of associated production can be accounted for by intrinsic parity alone; i.e. it would establish the physical identity of the origins of associated production and parity conservation in hadron processes.
This agreement between the predicted and empirically known two-hadron processes that are excluded from the subset of parity-conserving processes enables the interpretation of associated production as the empirical manifestation of the parity superselection generated by these processes.
It also provides the foundation for my explanation of the equality of the domains of validity of associated production and parity conservation as a manifestation of their physical identity.
11. Dynamics-Independent Breaking of Invariance under Space Inversion
Observation of the proposed processes that determine relative hadron parities would establish the relative sector parities of the initial and final states in parity-violating decays such as

to belong to neighboring parity-distinct sectors (see Sect. 5.3.2):

If the A+ is energetically stable against a parity-conserving decay such as (30), it would decay weakly into a nucleon and pions and, for a sufficiently large mass, into Ω‾, 2 π+.
An analysis of the operator

similar to that in Sect. 7.3 gives
i.e. ρmn is excluded from the set of observables compatible with P2 invariance.
The information available from a measurement is given as
I=Tr (ρ ln ρ) (44)
where ρ is the density matrix for the system.
The information available to an observer from a decay such as (41a) derives from two independent sources: (i) that from the measurement of this process itself, and (ii) that based on the properties of the decay system known to the observer from independent measurements. Collectively, this information includes (iii) knowledge of the initial state, | Σ+>, from its preparation; (iv) knowledge of the decay product in the second stage of the measurement process from its correlation with the measuring device in the third measurement stage; and (v) any information about the properties of the initial and final states in the observed decay obtained from other measurements; specifically, knowledge of their relative intrinsic parity from the measurement of those of their interactions that are compatible with P2 invariance. Observation of the decay (41a) provides directly the information required to identify the initial and final states in this decay. Additional information from this measurement is provided to the observer indirectly: according to (42a), the initial and final states in this decay have measurably different values of the phase of double space inversion P2. Measurement of this decay, therefore, breaks invariance under space inversion independently of the dynamics of the decay.
Experimental confirmation of processes such as (25) in Sect. 6.1 would thereby render breaking of P2 invariance in decays such as (41) to be a manifestation of measurement-generated symmetry breaking: a necessary, dynamics-independent consequence of the increase of information attendant to the measurement of a process connecting parity-distinct sectors [1,3].
The present empirical status of the dynamics-independent breaking of P2 invariance is compared with that for Galilean and rotational invariance in TABLE 6. The empirical context has been realized in the case of the former but not the latter.
| Symmetry | The essential phase difference in sector characterization; cannot be removed by a permissible phase change | The present empirical status of dynamics-independent symmetry breaking |
| Galilean invariance | mass-dependent factor in the phase for each sector is absolute | has been observed, e.g. in π-+ p → π -+ π+ + n |
| Invariance under rotations R | essentially different value of phase of R2π for integral (+1) and half-odd-integral (-1) spin states is absolute | not observed to date; the dynamics-independent breaking of rotational invariance would manifest itself in a process such as π+ → 2e+ + e- |
| Invariance under space inversion P | measurably different values of P2; absolute for neutral mesons; relative phase for baryons and charged mesons; e.g. ω, ω2=-1, for the neighboring sectors shown in TABLE 2 | parity violation in hadron decays has been observed; observation of the proposed processes will render such parity violation to be a manifestation of symmetry breaking attendant to measurements that connect parity-distinct sectors |
TABLE 6. Present status of dynamics-independent symmetry breaking.
The relative sector parity for unobserved decays, such as

The subset of potential observables whose measurement breaks space-inversion symmetry thus divides further into those with relative sector parity (ω, ω*; observed decays), and those connecting sectors with relative sector parity (–1, -ω, -ω*; unobserved decays).
Observation of strangeness-violating processes such as (25) would then determine the observed decays to be elements of the subset of observables connecting neighboring parity-distinct sectors; unobserved decays, such as (45a), to be elements of potential observables connecting parity-distinct sectors separated by one or more such sectors. This characterization of observed and unobserved decays is based on experimentally determinable ηs values.
In the currently accepted classification scheme, observed decays, such as (41a), are described phenomenologically in terms of change in strangeness S as |ΔS|=1; unobserved decays, such as (45a), as |ΔS|=2.
12. Restriction Principle
The structure of the proposed theory comprises several dynamics-independent elements: a formulation of particle interactions in terms of a set of observables subject to invariance under double space inversion P2, a symmetry operation that is a phase multiple of the identity; determination by these observables of sets of hadron states with the same electric charge and baryon number and measurably different values of this phase; restrictions on possible measurements consequent to its essentially different values; and characterization of parity-conserving hadron interactions by operators representing elements of reducible representations of the orthochronous Poincaré group.
Explanation of the physical identity of the origins of associate production and parity conservation on the basis of dynamics-independent concepts is indicative of the operation of a fundamental principle, one I term the restriction principle and formulate as follows.
The proposed parity-conserving hadron processes and their relations determine the phase e2iα of double space inversion P2 for distinct hadron states with the same electric charge and baryon number to have different values. They thereby divide the Hilbert space H of hadron states into parity-distinct sectors, sets distinguished by measurably different values of e2iα. The set A of Hermitian operators in H correspondingly divides into two mutually-exclusive subsets: the subset A1 with nonvanishing matrix elements connecting only states with the same value of e2iα, and the subset A2=A - A1 with nonvanishing matrix elements connecting only states with essentially different values of e2iα. Measurement of elements of A1 is compatible with P invariance. Measurement of elements of A2 necessarily breaks P invariance. The division of H into parity-distinct sectors thus generates an unconditional, dynamics-independent, purely theoretical restriction on possible measurements: the incompatibility of the concurrent operation of P invariance and the measurability of elements of A2. The consequent conditional restrictions on possible processes divide purely hadron observables into two mutually-exclusive restricted subsets of phenomena: those compatible with P invariance, which exclude A2, and those in A2, whose measurement must break this symmetry. Associated production is a manifestation of the exclusion of elements of A2 from the subset A1. Measurement of elements of A2, which include purely hadron decays that break associated production, must also break P invariance.
13. Summary and Conclusion
A theory has been proposed to explain the observed equality of the domains of validity of associated production and parity conservation in hadron processes as a manifestation of their physical identity. The current view involves two unrelated concepts -strangeness and parity -to account for the two phenomena and fails to account for this equality. In the proposed theory, invariance under a single symmetry, space inversion P alone, accounts for both phenomena.
The experimental test of the theory is provided by a set of processes that includes ones forbidden by strangeness but allowed by parity. Specific examples of such processes have been identified. Analysis of already recorded data may reveal their presence. Observation of these processes and the relations between them will determine the phases of P2 for distinct hadron states with the same electric charge and baryon number to have essentially different values. It will thereby establish baryon multiplets as parity multiplets, the nucleon as simply the lowest-mass such multiplet, and the kaon as the carrier of intrinsic parity between different parity multiplets.
All aspects of the theory -its basic underlying premise, its formulation, and its consequences -are structured entirely in terms of symmetry-based dynamics-independent concepts, a defining feature of algebraic quantum field theory. The theory is formulated in terms of a set of localized processes and the relations between them, the Hilbert space H of hadron states connected by these processes, and invariance under the Poincaré group.
The different relative phases of P2 for distinct hadron states divide H into parity-distinct sectors, sets of states within a given sector distinguished from those in a parity-distinct sector by measurably different values of these phases. Interactions in the proposed localized hadron processes thus change the structure of the multisector Hilbert space from one already divided into distinct sectors by the univalent, baryon, and electric-charge superselections operative in the noninteracting multihadron system into one divided additionally into the interaction-generated parity-distinct sectors in the case of the interacting system. The interactions are described by reducible representations of the Poincaré group. By generating parity-distinct sectors, they also change the nature of the operative group itself as well as that of its representations: from those for the restricted Poincaré group in the case of the noninteracting system, with multihadron states transforming according to direct products of its constituent representations and the operators representing this group transforming according to direct products of the operators representing the constituents, to those for the orthochronous Poincaré group (OPG) in the case of the interacting system, with states transforming according to its reducible representations and the operators representing this group transforming according to reducible representations that cannot be decomposed into direct products of operators for the noninteracting system.
Each parity-coherent sector of H serves as a separate representation space for operators representing the transformations of the reducible representations of the OPG that describe the localized hadron interactions. System interactions are reflected in the change in the structure of these operators from that for noninteracting systems. As the mass operator can be expressed in terms of the generators of temporal and spatial translations, M=(H2- P2)½, it should in principle account for the mass splittings between baryon multiplets, if they are due to the interaction. It will likely do so for multiplets with different numbers of baryons. But, because of invariance of the structure of the set of single-baryon states under a concurrent interchange of baryons among multiplets with the same number of baryons, an additional physical concept will seemingly be needed to account for the mass separations of the two doublets and of the two singlets.
Observation of the proposed strangeness-violating processes will establish associated production and parity violation in purely hadron decays to be mutually exclusive consequences of the incompatibility of the concurrent operation of P invariance and the measurability of processes connecting parity-distinct sectors: the exclusion of the subset of processes connecting these sectors from the subset of processes compatible with P invariance, and breaking of P invariance by processes connecting these sectors, respectively. The simultaneous breaking of associated production and parity conservation in purely hadron decays would reflect their common origin. Observation of the proposed processes would also render the introduction of a new quantum number to account for associated production to be unnecessary, and the prevailing assumption that an additively-conserved quantum number governs strong processes to be untenable.
The operation of a fundamental principle that explains the physical identity of the origins of associated production and parity conservation solely on the basis of symmetry-based dynamics-independent considerations has been formulated.
References
- Spitzer R. On neutral spin-0 particles with imaginary parity. Nucl Phys. 1961;21:681-85.
- Yang CN. Selection rules for the dematerialization of a particle into two photons. Phys Rev. 1949;77:242-45.
- Spitzer R. Symmetry-based dynamics-independent restrictions on allowed measurement. 2020;8:1-9.
- Samios NP, Plano R, Prodell A, et al. Parity of the Neutral pion. Phys Rev Lett. 1959;3:525-27.
- Orear J, Rosenfeld AH, Schlichter R.A. eds. Fermi E. Proceedings of the international conference, Nuclear Physics and the Physics of fundamental particles, September 17-22, 1951;109-10.
- Wightman AS. Superselection rules; old and new. Nuovo Cim. 1995;110B:751-69.
- Wick G, Wightman AS, Wigner E. The intrinsic parity of elementary particles. Phys Rev. 1952;88:101-5.
- Haag R, Kastler D. An algebraic approach to quantum field theory. J Math Phys. 1964;5:848-861.
- Brueckner K, Serber R, Watson K. The capture of π-mesons in deuterium. Phys Rev. 1951;81:575-78.
- Lamb WE. The interpretation of quantum mechanics, Rinton Press. 2001.
- Halpern F. Special relativity and quantum mechanics, Prentice-Hall, Englewood Cliffs, N.J. 1968:105-22
- Dirac PAM. The quantum theory of fields, proceedings of the twelfth conference on Physics at the University of Brussels, Interscience Publishers, New York, Oct. 1961:93.


