Original Article

, Volume: 11( 6) DOI: 10.37532/2320-6756.2023.11(6).353

• View PDF
• Download PDF

Anomalous Magnetic Moments of Proton and Electron as a Relativistic Effect of the Indeterminacy Relation

*Correspondence:

Yuriy Zevatskiy Independent Researcher, Ukraine , E-mail: yuri@newchem.ru

Abstract

Upon the Heisenberg indeterminacy principle, a bi-vector model of the ground (Gaussian) state of an elementary particle is proposed. A new interpretation of the observed physical value is proposed. It is shown that taking into account the relativistic mass leads to the appearance of an additional (angular) moment of momentum for particles in the ground state. The bad values of the magnetic moments of the proton and electron were calculated, and an acceptable fit to the observed data was reached. The alternative approach is proposed to determine the interconnections of a spin, angular and total moments of an elementary particle.

Keywords

Heisenberg indeterminacy principle; Gaussian

Introduction

The presence of bad values of the magnetic moments of the proton and electron until very recently plays an important role in the generation of quantum models. It is commonly known that considering the magnetic field anomaly of the electron as an objective phenomenon, Schwinger had laid the foundation for the relativistic quantum electrodynamics [1]. Using the observed values of the magnetic field of the electron in the analytical solution of the relativistic Dirac equation in the study [2], the Lamb shift for some transitions in the spectrum for hydrogen-like ions was calculated to high precision.

This study suggests to consider the deviations of the experimental values of the magnetic moments of the proton and electron from theoretical values, predicted by the Dirac theory, as a consequence of the presence of angular moments of particles in the ground (lowest-lying) states. This was indirectly mentioned by Born, who classified the lack of the additivity in calculating the deuterium nuclei moment from the moments of the proton and neutron as the absence of a pure S-state against the expected one [3].

Considering an elementary particle as a material point with r radius-vector and P momentum, special mention in this regard should be made of the value of their scalar product. Given the statistical character in defining of these values and introducing the traditional concept of the mean value, we can put down [4],

where r_m and P_m are vectors of mean values of the coordinate and momentum respectively. The square of the second term of the sum in the right side of the equality (1) is related to the product of the coordinate dispersions and momenta by the obvious relation,

According to the stability criterion in the middle position, the following equality is feasible,

Considering the stationary motion of a particle in polar coordinates, r 2 positional coordinate is required to be constant [5]. This is achieved provided,

According to the indeterminacy principle in the Heisenberg wording [4],

moreover, the equality is observed in a state of the minimal, the so-called Gaussian, indeterminacy. Thus, in the stationary Gaussian state of a particle, the following equality holds:

Hereinafter, atomic units will be used [6]. The fact that, due to the principle of the indeterminacy, a particle at rest, in the absence of interactions, has non-zero momentum and coordinates indicates that these values cannot be considered as ordinary vectors in the three-dimensional Euclidean space. Put it in another way, in the quantum consideration, three numbers are not enough to define the coordinate and momentum respectively. The development of this position is given below, taking momenta and coordinates as bivectors. In the context of this article, a bivector is defined as a pair of vectors, having a common tail at the origin. Moreover, any of these vectors can be obtained from the second one by the orthogonal transformation of coordinates. Therefore, according to the rules of the Euclidean space, the norms of this pair of vectors are equal. The norm of the bivector is adopted to be equal to the norm of its constituent vectors. It is further assumed that there exists a fixed axis, passing the origin and Ω angular velocity vector, directed along that,

where m is mass of a particle, and,

Substituting (7) for (6), and also using (8), we obtain,

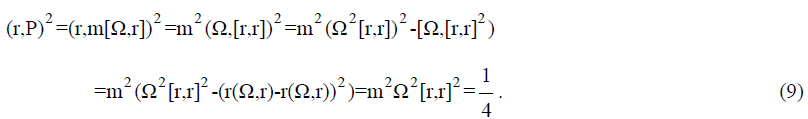
This equality indicates immediately to three facts. First of all, the impossibility to choose a fixed system of coordinates with an axis fixed in a space is the consequence of the indeterminacy principle. In other words, fixing any direction, it is necessary to consider the quantum phenomena with regard for the rotation around this direction with a certain finite angular velocity. The second is that the vector product of the coordinate itself does not become zero under any conditions, which is acceptable for bivectors. In other words, the scalar product of the radius-vector of a quantum particle by itself in any coordinate system turns out to be less than the square of its norm. And finally, the coordinate indeterminacy in the direction (bivector coordinates) is in the plane, perpendicular to the chosen fixed direction.

The equality (9) allows us to make some assumptions on the nature of the measured physical value. If a certain parameter, that has physical meaning, can be expressed as a bivector, then the scalar product of it by itself can be a potentially determined value of this parameter. Expressed in traditions of the Copenhagen school, the observed physical value can be only this one, the scalar product of which by itself does not become zero. Based on this assumption, it can be said that the momentum and coordinate of a particle in a stationary Gaussian state are not observable ones,

despite the fact, that norms of P and r values do not equal to zero. By contrast to this, the L momentum, which is defined as the vector product of the radius-vector by the particle momentum, is always observed at a non-zero norm.

The square of the particle’s rotary energy is an essentially positive value,

Since even at the zero momentum (in a stationary Gaussian state) it is not equal to zero. This means that, being at the lowest rotational level, the particle has some finite rotation energy, analogous to the behavior of a quantum oscillator at the zero vibrational level. The latter circumstance eliminates the longstanding controversy between the old quantum theory and the patterns, detected in the rotational (IR) spectra of molecules [7]. We obtain a similar equality for scalar and vector products of momentum, the sum of whose squares do not become zero,

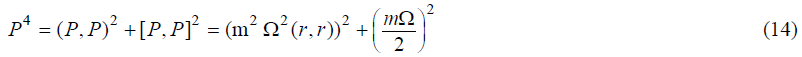
The Einstein equation in atomic units is written as follows,

where α is a Sommerfeld constant (of a thin structure), Pe is a kinetic momentum of a particle, m0 is a mass of a particle at rest. The fundamental assumption in the proposed model is to define the relationship between the elements of the equalities (14) and (15). One option is to consider the momentum, appearing on the left side (14) and the full (relativistic) momentum, on the left side (15) as equal. By isolating the constants, we find the following, 2

which exactly coincides with the frequency of the so-called trembling motion of the relativistic particle (Zitterbewegung according to Schrodinger). The energy of the indicated motion is equal in the magnitude to the energy of the mass of a particle at rest. Let us introduce the λ notation for the Compton wavelength of a particle in atomic units,

Carrying out algebraic transformations, we obtain the following expression for the norm of L momentum,

Considering the scalar product of the bivector by itself as the value observed in experiments, we can associate it with the full elastic scattering cross-section of a particle by the same particle, obtained in the limit of zero kinetic energy of the motion,

where u is non-dimensional fixed coefficient. Reasons for this are obvious and lie in the small perturbation process, introduced into the ground state of the particle under the interaction with the like particle with a low W (kinetic energy). The second is that the indicated scattering is entirely determined by the zero phase of η0 S-scattering, moreover the full effective cross-section is equal to [8, 9]:

The a scattering length is independent of energy of the incident particle W. The third fundamental principle is based on the fact that under the collision of identical particles, the scattering cross-section is determined entirely by the parameters of their structure.

The experimental data on the scattering length of slow protons by protons from studies [9-12] are given in the Table 1:

Using the mean value in (20) and assuming u=2.34×10^-14 in (19), according to the formula (18) we get for the proton,

The indicated angular momentum value, taking into account g-factor equal to 1 contributes to the proton magnetic moment in the amount of 1.97 of the nuclear magneton. It differs from the experimental value of 1.792847337 by less than 9.7% [13].

In the literature the data on the electron-electron scattering is given in the form of the dependence of differential cross-sections on the kinetic energies of electrons. In this case, the scattering lengths can be obtained by the extrapolation using the effective radius method [9, 14]. The transition from the differential cross-section to the zero scattering phase was calculated in the scattering approximation by the Coulomb field barrier [9]. TABLE 2 shows the results of the calculations based on experimental data with the indication of energy rang of incident electrons [15-17].

Substituting this value in (20), and then in (19) and (18) for u=2.34×10^-14, we obtain,

which, setting g-factor equal to 1, contributes to the magnetic moment of the electron of 0,00107 Bohr magneton. The comparison with the observable quantity, equal to 0.0011596521869 [13], reveals a discrepancy by 7.7%.

Using formulas (14)-(16) and (18), it is possible to find the values of the β relativistic coefficients, i.e. the ratio of the kinetic momentum to the total momentum of the particle, at which the calculated angular moments will correspond to experimental ones.

By substituting values of moments from [13], we obtain,

for the electron, and,

for the proton. Such a key difference between the fraction of the kinetic momentum of a proton and the analogous fraction of an electron can be interpreted by the Hertz concept on the kinetic origin of the potential energy as follows [18]. Considering the momentum and angular momentum in the ground states of particles as a result of hidden motions in cyclic coordinates, in other words, using the terminology of quantum physics, excluding the degree of the freedom of the particle associated with the spin, we obtain the presence of a potential field, that is quite significant as for the proton and inappreciable as for the electron. The radius of action of forces of the indicated field of the order of the Compton wavelength of a particle as well as the discussion of the field character is beyond the scope of this article.

The last remark concerns one more outcome of the formula (6). If a particle has a nonzero momentum in a steady Gaussian state, the following relation holds, which leads out of vector rules,

Introducing, according to Dirac, j as the integral of the total momentum, we have,

It is a direct consequence of the quantization law for the operator of the square of the angular momentum of the particle,

Introducing s spin integral for states in which the minimum uncertainty is not achieved, the formula (27) is transformed to [4],

where l is an integral of the angular momentum, s=0 for Gaussian conditions. The resulting equality is equivalent to the generally accepted law on the addition of squares of momentum operators, expressed in terms of the eigenvalues of operators.

Thus, associating the spin of the particle with the scalar product of the momentum and the coordinate in the Gaussian state of the particle, certain co-relations, associating squares of the total, angular and spin momentum, are obtained.

Conclusions

It is allowed to consider the spin not only as an operator in the form of Pauli matrices, but also as a scalar product of the momentum and coordinate of a particle in a steady Gaussian state. This assumption does not contradict a number of experimental facts and some provisions of the quantum theory. The advantage of this proposal consists in the obviousness of the angular momentum quantization rule, while there is no need to determine the angular momentum norm as l(l+1) under the l maximum value, its projection onto the spatial axis.

Anomalous values of the electron- and proton-magnetic moments can be considered as a demonstration of the angular momenta in the ground states associated with the spin to the utmost degree by the relativistic effect of the mass variation.

For physical values, represented as bivectors, it is suggested to introduce the concept of the observed value. Thus, a value is numerically equal to the square root of the scalar product of the value by itself. Due to the indeterminacy principle, this value is far from being always equal to the norm. The equality always holds in the limit of ħ→0.

It is shown that it is impossible to choose a non-rotating reference frame with a fixed axis in a space, while describing the states of a quantum particle. The frequency of rotation of the system is equal to the frequency of the trembling motion (Zitterbewegung).

An obvious drawback of the proposed model is that it implies that the particle has a m0 certain hypothetical rest mass, which it would possess in the limit of β→0. For an electron, this hypothetical rest mass is comparable with the observed one and is equal to 0,999997 atomic units of the mass. As for the proton, a rest mass 3.72 times lower than the observed one, i.e. approximately 493 amu, should be attributed to it. Unfortunately, at the time being the author has no opportunity to verify this provision.

It is planned to increase the accuracy of this method by establishing a stricter link between values, occurring in (14) and (15) that is between the observed and relativistic momenta. In addition, as an observed value (r, r) we can suggest using some other experimental parameter related with the linear dimensions of the particle.

References

1. Ramsey N. Molecular beams. Oxf. Univ. Press; 1956.

   [Google Scholar] [Crossref]

2. Zevatskiy Y. Anomalous Magnetic Moments of Proton and Electron as a Relativistic Effect of the Indeterminacy Relation. Available at SSRN 4418876. 2023

   [Google Scholar] [Crossref]

3. Born M. Atomic Physics. London: Blackie, 1935. [Google Scholar] [Crossref]
4. Holevo A. S. Statistical structure of the quantum theory. Moscow-Izhevsk: Institute of computer science, 2003;14, 33, 41. [Google Scholar] [Crossref]
5. Gantkhamer F. R. Lectures on analytical mechanics. M.: Fizmatlit, 2002;249. [Google Scholar] [Crossref]
6. Fok V. A. Introduction to the quantum mechanics. M.: Science, 1976; P. 193. [Google Scholar] [Crossref]
7. Hertzberg G. Molecular Spectra and Molecular Structure: I. Spectra of Diatomic Molecules. Krieger, 1989. [Google Scholar] [Crossref]
8. Mac Daniel I. Collisions in ionized gases. Wiley, 1964. [Google Scholar] [Crossref]
9. Mott NF, Massey HS, The International Series of Monographs on Physics. The theory of atomic collisions. Oxf. Clarendon Press; 1965  

   [Google Scholar] [Crossref]

10. Brolley J.E. Aust. J. Phys., 1969;22:332.  [Google Scholar] [Crossref]
11. Zevatsky Yue. ANOMALOUS MAGNETIC MOMENTS OF THE PROTON AND ELECTRON AS A RELATIVISTIC EFFECT OF THE UNCERTAINTY RELATIONSHIP. Proc. St. Petersbg. State Technol. Inst. (Tech. Univ). 2007(1):10-3.

    [Google Scholar] [Crossref]

12. Jackson J.D, Blatt J.M. The Interpretation of Low Energy Proton-Proton Scattering Rev. Mod. Phys., 1950;77(22):109. [Google Scholar]

    [Crossref]

13. Mohr P.J., Taylor B.N. Physics Today, 2003;8:9,10. [Google Scholar] [Crossref]
14. Zemke WT, Das G, Wahl AC. Theoretical determination of the electron affinity of O2 molecule from the binding energy of O− 2. Chem. Phys. Lett. 1972;14(3):310-4.

    [Google Scholar] [Crossref]

15. Page L.A., Woodward W.M. Phys. Rev., 1950;79(1);228. [Google Scholar] [Crossref]
16. Page L.A. Phys. Rev., 1951;81(6);1063.  [Google Scholar] [Crossref]
17. Ashkin A., Page L.A., Woodward W.M. Electron-Electron and Positron-Electron Scattering Measurements. Phys. Rev., 1954;94(2):360. [Google Scholar] [Crossref]
18. Hertz H. The principles of mechanics presented in a new form. Macmillian Co. Ltd; 1899.

    [Google Scholar] [Crossref]