Review

, Volume: 6( 3)

• View PDF
• Download PDF

An Approach of a Fluid Dark Matter with the Classical Λ-Term

*Correspondence:

Hebzibha Isravel , 9 M.T ech. Aerospace Engineering, Karunya University, Coimbatore, Tamil Nadu-641114, India, E-Mail: hebzi.hebzi@gmail.com

Abstract

A cosmological model considering the dark matter as an isotropic fluid and embracing the influence of the cosmological constant in the flat Robertson-Walker metric is investigated. The acquired Equation of state (EOS) parameter confess the omnipresent natural property of the overall matter content in the present cosmos corroborating with the cosmic coincidence problem. It also exhibited its influence on the incidence of the finite singularity in the future called the Big Rip. The cosmic acceleration as a function of the redshift (Z) and the EOS parameter is extrapolated and compared with few coherent models for analysing its correlation.

Keywords

Dark matter; Equation of state; Perfect fluid cosmology; Big Rip singularity; Acceleration expansion

Introduction

Ever since it has been discerned that there is an escalation in mass-to-light ratio detected by the virial theorem and galactic flat rotation curves in the clusters of galaxy [1], predictions demanded the predominant existence of an unidentified sort of a matter termed as “dark matter” in the galaxies’ halo and also it is harmonised by diverse phenomena such as weak gravitational lensing by galaxy clusters, velocity dispersion in galaxy clusters, hydrostatic equilibrium of X-ray emitting gas, COBE, and WMAP [2]. However it is imperceptible, its dominance can be indicated by its exertion of gravitational force upon the visible luminaries [3]. Henceforth it has become an undeniable core area of research in the field of Astronomy and Astrophysics.

Therefore, several cosmological models of the early as well as the later universe have been suggested for the examination of the characteristics and properties of the dark matter. Among which the ΛCDM model demonstrated the theoretical consistency with the observed measurements of the WMAP and the cosmic microwave background (CMB) at the cosmological scale whereas at the galactic scale it undergoes many serious contradictions due to its assumption of a pressure 2
less dark matter fluid even though it can be validated on some occasions for example if the properties of the matter are of weakly interacting massive particles (WIMPs) [4]. In spite of this, a perfect fluid model is also an acceptable model convincing it’s sustenance by satisfying required observational mass and EOS in an individual expression [5] while it is derived from the isotropic fluid formula [6]. In a perfect fluid model instead of Λ (where the cosmological constant (Λ) is related to the dark energy inhabiting 70% of the overall energy of the universe), the Hubble parameter dependent bulk viscosity coefficient (μ (H)) adjacent to ΛCDM is proposed by [7] whereas the singularity of the Hubble parameter varies because of the existing dark matter [8].

Cosmic expansion acceleration is quite a parameter that is associated with the modelling of the universe since it expresses the present progression of the large-scale structure. In the perfect fluid model, it can be explained theoretically with the interval of Z to expound the observational expansion of the universe [7] and also without the influence of the Λ term and the fluid pressure, the instigation of acceleration with only an effective viscosity under certain conditions is also rather possible [9]. An unstoppable acceleration of the universe can be achieved if the assumption of hydrodynamics hinged with bulk viscosity is also put forth to mull over [10].

In this Letter, a simple cosmological model formulated from the Robertson-Walker metric with the assumption of dark matter behaving as an isotropic fluid (due to its property to satisfy the observations at stellar and cosmic scales) involving the non-zero Λ-term is considered. The deceleration parameter q is derived as a function of EOS parameter(ω), Hubble parameter and Z. An overall scaling of the Hubble parameter with the redshift to suggest a specific interpretation of the early to future acceleration of the expanding universe and then the assessment of the comparison of previously recommended widespread models is deliberated.

A Cosmological Model Interpolation

Let the (flat) Robertson-Walker line element be

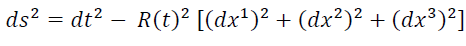. (1)

where R(t) is the expansion parameter.

The Einstein field equations can be written in the form:

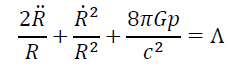, (2)

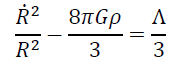. (3)

Where R is a time-dependent scale factor, p is the pressure, ρ is the energy density and Λ is the cosmological constant.

Energy conservation equation for the above metric can be written as,

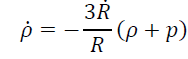(4)

From the above equation, we can get

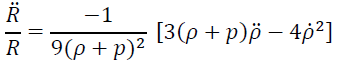. (5)

By substituting equations (4, 5) in equations (2, 3) and integrating, one can easily obtain the following:

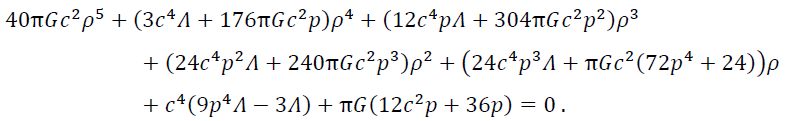(6)

 

Whereas the EOS for the isotropic perfect fluid is of the form p = ωρ and substituting this in above equation, we yield

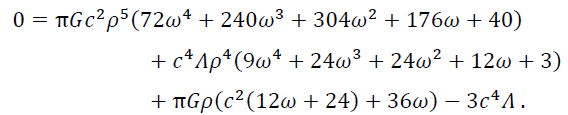(7)

where ω is an EOS parameter. Now from the above expression by substituting all the ascertained values of the specified variables, ω can be determined as

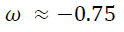(8)

The value of ω reveals that there is a probable prevalence of phantom regime ( ω < - 1) where the fluid drifts into and at this region the dark fluid exhibits a performance correlated to quantum fields [11]. Hence, paving the way for a finite time singularity called the Big Rip phenomena consists of some mysterious properties in the cosmological evolution which could occur in the future [12]. It correspondingly stating that in a certain manner dark matter and dark energy both are knitted together which can only be confirmed by further observations because ω is less than the unity is usually denoted for the dark energy parameter. Depends upon the kind of cosmological matter present, the rips can be of different types by impelling one or more physical quantities to become infinity. In a more general case, it is defined by ρ = ∞. This in turn causes the incidence of negative entropy [13] and dissipation [14,15]. As a result of the negative ω , EOS here resembles the exotic fluid model named as the Chaplygin gas obtained by combining the dark matter and dark energy heuristically [16], however it is accomplished without the inclusion of the Λ -term. With Λ= 0 in the Flat metric of the later universe dark fluid model, it may be possible to cross the barrier between phantom (ω < 1) and quintessence region (ω > 1) by the inclusion of bulk viscosity [17].

Acceleration Expansion of the Universe

A cosmic expansion in the universe has exposed an acceleration when it is perceived over a time period has been witnessed under a number of cosmological observations [18]. While in the current phase, the acceleration is relayed from the early epoch of deceleration and by the real-time observations of expansion over past years, it is established that these two epochs shifts at Z = 0.46 ± 0.13 [19]. Hence beyond this transition value, the future or a present time expansion can be manipulated. The magnitude of the deceleration parameter is generated from:

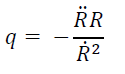(9)

We know that 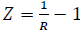and thus from the equations (4) and (9). q is gained as

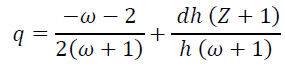(10)

The expression has been extrapolated for the existing as well as the future acceleration and it demonstrated a far-fetched uniformity with the observation for the present time epoch where at q = -0.6, h should be 1.

The models are compared in the FIG. 1 wherein from the argument of transition from the deceleration zone, the Equ. (10) has closely allied with the ΛCDM model and also the viscous dark fluid model (It should be noted that they have deduced without the -term but utilized Ω^Λ to prove their consistency with the ?CDM). It is also extrapolated beyond the value of q = -0.6 corroborates the past deceleration and it shows a narrow margin with the ?CDM and the observed values within the confidence level [20]. The Hubble parameter dependant viscosity model has a similar extrapolation except for the EOS parameter in it and the Λ - term. The deviation between the present model and the Viscous Model is provoked due to these entities although it had shown a marginal similarity to it. The bulk viscosity has been added for the broader comparison yet it imposes a larger deviation. Interestingly, all the models culminate with an empty static ?The de Sitter? universe affirming that at a certain specific future time the expansion will, on the whole, be ceased.

Conclusion

In the summary, a fluid cosmological model of the matter that lurks in the halo of the galaxies of the universe taking into account the cosmological constant in the Robertson walker flat space-time is probed. The achieved EOS parameter had a negative magnitude evidencing that the negative pressure is ubiquitous in the universe concurrently it is also less than -1 implying that dark energy and the dark matter are interwoven in some mysterious fashion. It can be defended by the cosmic coincidence problem which attests that the ratio of dark energy and dark matter are unity but contradictorily describes them as two individual factors [21] and it could be the reason for the emerging unified dark fluid models recently. It also indicates that the fluid slips into the phantom region and prompts a future finite time singularity called the Big Rip. Further, when the acceleration expansion of the universe is derived from the fluid approach compared with the compatible models, a notable correlation with the ΛCDM model and observations within the specified range of redshift representing the past, current, and future epochs. A further study extending on the curvature space or by implementing the fluid mechanics in the model presented can be executed in the future.

References

1. Sikivie P. Sources and distributions of dark matter. Nuclear Phys B-Proc Suppl. 1995;43:90-9.
2. Strigari LE. Galactic searches for dark matter. Phys Rev. 2013;531:1-88.
3. Bertone G, Hooper D, Silk J. Particle dark matter: Evidence, candidates and constraints. Phys Report. 2005;405:279-390.
4. Chavanis PH. The Logotropic Dark Fluid as a unification of dark matter and dark energy. Phys Lett B. 2016;758:59-66.
5. Potapov AA, Garipova GM, Nandi KK. Revisiting perfect fluid dark matter: Observational constraints from our galaxy. Phys Lett B. 2016;753:140-6.
6. Rahaman F, Nandi KK, Bhadra A, et al. Perfect fluid dark matter. Phys Lett B. 2010;694:10-5.
7. Folomeev V, Gurovich V. Viscous dark fluid. Phys Lett B. 2008;661:75-7.
8. Elizalde E, Obukhov VV, Timoshkin AV. Inhomogeneous viscous dark fluid coupled with dark matter in the FRW universe. Modern Phys Lett A. 2014;29:1450132.
9. Ren J, Meng XH. Cosmological model with viscosity media (dark fluid) described by an effective equation of state. Phys Lett B. 2006;633:1-8.
10. Gagnon JS, Lesgourgues J. Dark goo: Bulk viscosity as an alternative to dark energy. J Cosmol Astroparticle Phys. 2011;2011:026.
11. Nojiri SI, Odintsov SD. Quantum de Sitter cosmology and phantom matter. Phys Lett B. 2003;562:147-52.
12. Caldwell RR, Kamionkowski M, Weinberg NN. Phantom energy: dark energy with w<- 1 causes a cosmic doomsday. Phys Rev Lett. 2003;91:071301.
13. Brevik I, Nojiri SI, Odintsov SD, et al. Entropy and universality of the Cardy-Verlinde formula in a dark energy universe. Phys Rev D. 2004;70:043520.
14. Prisco DA, Herrera L, Ibanez J. Qualitative analysis of dissipative cosmologies. Phys Rev D. 2000;63:023501.
15. Herrera L, Di Prisco A, Ibanez J. On the dual interpretation of zero-curvature Friedmann-Robertson-Walker models. Classical Quantum Gravity. 2001;18:1475.
16. Kamenshchik A, Moschella U, Pasquier V. An alternative to quintessence. Phys Lett B. 2001;511:265-8.
17. Brevik I, Gorbunova O. Dark energy and viscous cosmology. Gener Relativity Gravitation. 2005;37:2039-45.
18. Bahcall NA, Ostriker JP, Perlmutter S, et al. The cosmic triangle: Revealing the state of the universe. Sci. 1999;284:1481-8.
19. Riess AG, Strolger LG, Tonry J, et al. Type Ia supernova discoveries at z> 1 from the Hubble Space Telescope: Evidence for past deceleration and constraints on dark energy evolution. The Astrophys J. 2004;607:665.
20. Alam U, Sahni V, Starobinsky AA. The case for dynamical dark energy revisited. J Cosmol Astroparticle Phys. 2004;2004:008.
21. Fitch VL, Marlow DR. Critical Problems in Physics: Proceedings of a Conference Celebrating the 250th Anniversary of Princeton University, Princeton, New Jersey, October 31, November 1 and 2, 1996. Princeton University Press; 1997.