Current opinion
, Volume: 10( 3) DOI: 10.37532/2320-6756.2022.10(3).266Alternate Proof For Expression of Most Probable Speed of Gas
- *Correspondence:
- Veeresh Kodekalmath
REVA University, Bengaluru, Karnataka, India
E-mail: mathveeresh168@gmail.com
Received: March 05, 2022, Manuscript No. tspa-22-56228; Editor assigned: March 07, 2022, PreQC No. tspa-22-56228 (PQ); Reviewed: March 25, 2022, QC No. tspa-22-56228 (QC); Revised: March 26, 2022, Manuscript No. tspa-22-56228; Published date: March 30, 2022, DOI: 10.37532/2320-6756.2022.10(3)266.
Citation: Veeresh Kodekalmath, Lternate Proof For Expression of Most Probable Speed of Gas. 2022;10(3):266.
Abstract
Introduction
Most probable speed is the speed most likely possessed by any gas(of the same mass) in the system.It can be derived using Maxwell- Boltzmann distribution function [1] for ideal gases.I will provide an alternate derivation by using the definition, gas laws and kinetic theory of gases.
Preliminaries
Boyles’s law:The absolute pressure exerted by given mass of an ideal gas is inversely proportional to the volume it occupies if the temperature and amount of gas remains unchanged with in a closed system [2]. In an elastic collision the total kinetic energy of the system is constant [3].
Main Result
The most probable speed of the gas is given by,
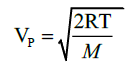
whereVP is the most probable speed of the gas, R is the universal gas constant, T is the absolute temperature of the system and M is the molecular mass of the gas. Proof:Consider a given amount of ideal gas in a closed system at constant temperature. By Boyl e’s
pv = constant
and for a given amount of gas and at constant temperature by assumptions of kinetic theory of gases
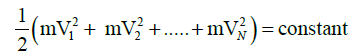
since equation one and two are constant for same parameters and dimensionally energies,we can equate them
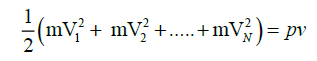
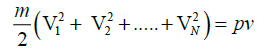
,using the definition of most probable speed,lets say all of the molecules are moving with VP
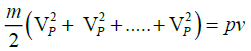
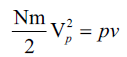
,where N is the total number of molecules and Nm is the mass of the gas
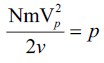
But,
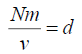
,d=density of the gas
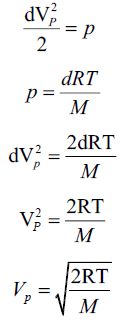
hence proved.
Acknowledgment
I would like to thank my friends Dani vinayak,Vidya,Abhinav who listened to my ideas carefully and encouraged me constantly.
References
- F. Mandl, Statistical Physics, Manchester Physics, 2nd Ed., John Wiley and Sons, 2008.
Google Scholar Crossref - Levine, Ira N. ”Physical Chemistry” University of Brooklyn: McGraw-Hill, 1978.
Google Scholar Crossref - Craver, William E. Elastic collisions. 2013.
Google Scholar Crossref

