Original Article

, Volume: 11( 4) DOI: 10.37532/2320-6756.2023.11 (4).340

• View PDF
• Download PDF

A simple formula that allows to calculate the curvature of the trajectory in the Minkowsky space-time of a point located at a fixed distance from a point mass

*Correspondence:

Fernando Salmon Iza
Bachelors in Physics from the Complutense University of Madrid UCM, Spain
E-mail: fernandosalmoniza@gmail.com

Abstract

A formula that allows calculating the curvature of the trajectory in the Minkowski space-time (scalar curvature) of a point in the case of a gravitational field caused by a point mass, through the values of mass and spatial distance.

Keywords

Cosmology; General relativity; Curvature of space-time

Introduction

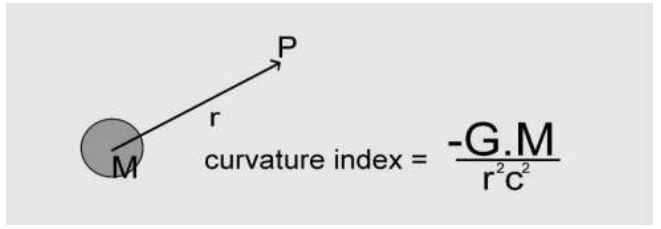
Starting from a point mass "M" we study the curvature of the trajectory in the Minkowski space-time (scalar curvature) of a point away from the mass “M” a distance "r".

Training the Formula

According to rational mechanics, the centrifugal acceleration to which a mobile is subjected that travels around a curve at a speed "v" in a trajectory with a radius of gyration R, is given by:

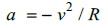
According to the general theory of relativity, the gravitational field is created due to our motion in curved space-time, just like centrifugal force when we are traveling in a car around a curve. If, as we know, space-time moves at a speed of module "c", an observer who is at rest near a mass will be subjected to a gravitational field created by that mass "M", a field that curves space-time, and will experience, due to the speed "c" of space-time and the curvature of space-time, a centrifugal acceleration "a" given by:

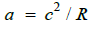
where R is the radius of curvature of the path of that point in space-time. The force to which it is subjected is given by

This force to which it is subjected is experienced as a gravitational force and according to Newton's theory of gravitation it is also expressed as

where G is the universal gravitational constant.

Equating the two expressions (1), (2) we obtain:

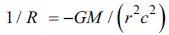
1/R turns out to be the index of the scalar curvature (curvature of the Minkowski space-time trajectory) from a fixed point at a distance "r" from a point mass M.

A formula that allows us to calculate the scalar curvature of the trajectory in space-time of a point, at a spatial distance "r" from a point mass "M", based on parameters that are easy to determine, such as mass and spatial distance. FIG. 1

A Calculation with Imagination

We are going to calculate the curvature of space-time at the radius of the observable universe and with a mass equal to the total mass of the universe. Let's see the result:

Radius of the observable universe 4.40 × 10²⁶ m [1].

Mass of the universe 9.27 × 10⁵² kg

G constant of universal gravitation 6.67 × 10^-11 Nm² / Kg²

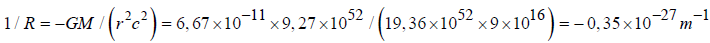
Value close in order of magnitude to that of the vacuum energy density 0.6 × 10^-26 Kg / m³ [2].

Conclusions

For an assumption of a point mass, a simple formula has been obtained that allows calculating the index of the scalar curvature (curvature of trajectory in the Minkowski space-time) of the point (t, r), where r is the spatial distance to the mass "M" that is causing that curvature, depending on that distance and the value of that mass.

References

1. Espanol WH. Org. pluricelular,

   [Google Scholar] [Crossref]

2. Prat J, Hogan C, Chang C, et al. Vacuum energy density measured from cosmological data. J. Cosmol. Astropart. Phys. 2022(06):015. [Google Scholar]

   [Crossref]