Research

, Volume: 11( 3) DOI: 10.37532/2320-6756.2023.11(3).327

• View PDF
• Download PDF

A New Interpretation of Thomas Young Refractive Index Law n=c/v

*Correspondence:

Abdelkrim Alileche
Boise State University, Biology Department, 1910 University Drive, Boise ID 83725, USA
Tel: +12089977227
E-mail: abdelkrimalileche@boisestate.edu

Abstract

The Thomas Young refraction law established in 1807 needs a new evaluation. So far this law, simple in its formulation n=v/c, has been applied only when light passes from low refractive index medium like air to a high refractive index medium like glass and never when light exits back to air. New developments like the slowing down of light up to 17 ms-1 by Lene Hau and others, and the widespread use of optic fibers to transmit a huge amount of all kind of information and the Internet around the world, mandates the new evaluation. The matter at hand is whether we apply this law when light exits from glass to air, or we need a new formulation of the Thomas Young law for its new application.

Keywords

Young law; Refractive index medium

Thomas Young, James Maxwell and Max Planck

It was Thomas Young who introduced the refractive index of a condensed medium like water, glass, diamond and any liquid with this equation n=c/v [1]. c is the speed of light in vacuum and v is the speed of light in water, glass or any other medium. So far the Young law was applied when light goes from a low refractive index like air to high refractive medium like water, glass or diamond. There is a general agreement the speed of light is lower than in vacuum. It seems to me necessary to investigate the behavior of light when exiting from a high refractive index like glass or other condensed medium to a low refractive index like air. I mean what happens to the physical parameters of light (speed, frequency, wavelength and energy). As for the frequency and energy (linked together in Planck law E=hν), they both diminish during refraction [2, 3]. The un-answered question remains what happens to the speed of light upon exit from glass to air. I think this issue had never been addressed theoretically and experimentally checked in scientific literature and in physics manuals. There is a general consensus based on many ideas that light recovers its vacuum speed. Since during refraction light keeps its frequency as it was before refraction, and thanks to Planck law E=hν, its energy is the same, therefore upon exit light recovers its vacuum speed. Well, it is necessary to remember according to James Maxwell the speed of light in vacuum is independent of the frequency of light and therefore of its energy [4]. All electromagnetic waves from radio waves to gamma rays have the same speed.

A New Interpretation of Thomas Young Refraction Law

• This law is valid when light moves from low refractive index medium like air to high refractive index like water, olive oil, glass, diamond and many others.

• This law is valid when light moves from a high refractive index medium like water, olive oil, glass, diamond and many others, to a low refractive index medium like air and even vacuum.

• The Thomas Young law is aimed at establishing the refractive index of the medium in which the light refracts in and not the refractive index of the medium the light is coming from.

• This extension of validity of the refraction law of Thomas Young as stated previously will open new areas in the world of optics and physics in general

The speed of light upon exit from a high refraction index medium to a low refraction index medium

Let’s consider the following experiment in which light comes from air, refracts in glass and exits from glass to air again. In air the speed of light (c) is 3×10⁸ ms^-1. In glass (refractive index 1.5) the speed of light is 2×10⁸ ms^-1. Therefore the glass refraction index according to Thomas Young n=c/v=3×10⁸/2×10⁸=1.5. When light exits glass to air, the Thomas Young law is applied the same way as when light goes from air to glass. The refraction index of air is 1. We can no longer consider the speed of light in vacuum, instead we should consider the speed of light in glass, let’s call it vg. The speed of light after exit from glass to air is called vex. The exit speed of light becomes after applying the Thomas Young law: n=v_g/v_ex=1. Therefore after a strict application of the Thomas Young law, upon exit from glass to air, the exit speed of light in air is the same as its speed in glass [5-9].

Effect of the new interpretation of the Thomas Young law on the evolution of the frequency of electromagnetic waves during refraction and exit from it

Since the exit speed of light is the same as the speed of light during refraction, the exit light frequency will diminish as it is shown here. Before refraction the light frequency ν₀ is defined by the Planck law E_air=h×ν₀. During refraction the light frequency ν_g diminishes because of the Lorentz contraction E_r becomes [10],

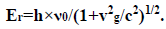
After exit from glass to air, the light energy becomes Eex and the light frequency becomes νex,

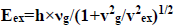
And since,

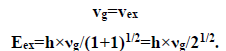
This is a confirmation of a previous paper [11].

Dedication

I would like to dedicate this paper and the Lorentz paper to two institutions in Boise ID, USA:

• To the Boise Public Library

• To Goldy's institution. To Wanda, Randy and Goldy's wonderful team.

References

1. Young T. A course of lectures on natural philosophy and the mechanical arts: in two volumes. Johnson; 1807.
2. Alileche A. A Theoretical Assay on the similarity of Light Refraction in a medium and the Compton Effect J. Phys. Astron.2022;10(9):296
3. Alileche A. Theoretical Assay on the Quantization of the Waves of Electromagnetic Waves Based on Logarithmic Analysis J. Phys. Astron.2022;10(9):295
4. Maxwell JC. VIII. A dynamical theory of the electromagnetic field. Philos. trans. R. Soc. Lond.1865(155):459-512.
5. Hau LV, Harris SE, Dutton Z, et al. Light speed reduction to 17 metres per second in an ultracold atomic gas. Nature. 1999;397(6720):594-8.
6. Liu C, Dutton Z, Behroozi CH, et al. Observation of coherent optical information storage in an atomic medium using halted light pulses. Nature. 2001;409(6819):490-3.
7. Kash MM, Sautenkov VA, Zibrov AS, et al. Ultraslow group velocity and enhanced nonlinear optical effects in a coherently driven hot atomic gas. Phys. Rev. Lett. 1999;82(26):5229.
8. Brehm JD, Gebauer R, Stehli A, et al. Slowing down light in a qubit metamaterial. Appl. Phys. Lett. 2022;121(20):204001.
9. Bons PC, De Haas R, De Jong D, et al. Quantum enhancement of the index of refraction in a Bose-Einstein condensate. Phys. rev. lett. 2016;116(17):173602.
10. Alileche A. Lorentz contraction of the frequency of electromagnetic waves (EMWs) during refraction submitted to J. Phys. Astron.2023;11(3):326
11. Alileche A.A theoretical assay on the similarity of light refraction in a medium and the Compton effect J. Phys. Astron. 2022;10(9):296